矩形MQAM SFBC-OFDM系统的误码性能
2010-11-26王成英李光球
王成英,李光球
(杭州电子科技大学通信工程学院,浙江杭州310018)
0 引 言
衰落信道上的多径衰落严重恶化了多输入多输出无线通信系统的性能。正交频分多路复用(Orthogonal Frequency Division Multiplexing,OFDM)能将频率选择性信道转换成一组平坦衰落信道,减小多径衰落的影响。为了同时获得空间分集和频率分集,文献1提出了空频分组编码(Space-Frequency Block Coding,SFBC)OFDM系统。文献2研究了快衰落信道上具有理想信道状态信息(Channel State Information,CSI)的SFBC-OFDM系统的平均误比特率(Bit Error Rate,BER)性能,文献3推导了瑞利衰落信道上具有理想CSI的方形M进制正交幅度调制(M-ary Quadrature Amplitude Modu lation,MQAM)SFBCOFDM系统的平均BER解析表达式。文献4推导了瑞利衰落信道上有信道估计误差的采用方形MQAM调制SFBC-OFDM系统的平均BER近似解析表达式。矩形MQAM调制解调比较简单,在给定最小距离的情况下,所需的平均功率仅比最好的MQAM信号星座的平均功率稍大,其特殊情况是方形MQAM[5]。为此,本文研究瑞利衰落信道上有信道估计误差的矩形MQAM调制SFBC-OFDM系统的误码性能,目前尚未见有研究报道。
1 系统模型
具有nT个发射天线、nR个接收天线的SFBC-OFDM系统如图1所示,与文献4不同的是本文考虑矩形MQAM调制。
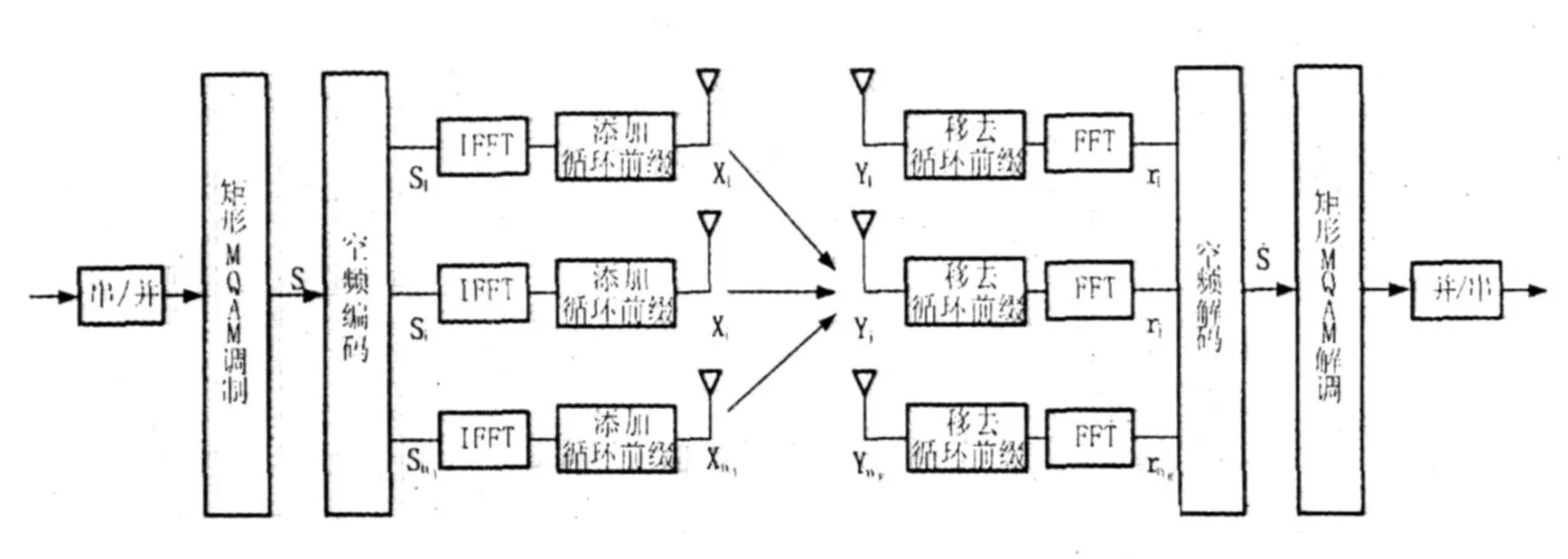
图1 SFBC-OFDM系统模型
假定OFDM的子载波数为,且被分为Ns个子带,每个子带包含v个相邻的子载波,所有的子带均采用矩形MQAM调制,其中v是SFBC编码器的符号间隔,Ns=K/v。SFBC编码器的输入信号为经过串/并变换和调制映射的矩形MQAM信号,SFBC编码器的输出信号被映射为nT个并行数据流S1,S2,…,SnT,长度均为K且包含K/v个子块,于是有Si=(si[0],si[1],…,si[K/v-1])T,i=1,2,…,nT,其中si[◦]是SFBC编码矩阵中包含v个子载波的子块。以2发1收、采用编码方式的SFBC-OFDM系统为例,SFBC编码器的输入信号为S=(s[0],s[1],…,s[K-1]),对OFDM的每两个相邻子载波和两个发射天线上的信号进行G2编码,编码后,得到两个信号S1=(s[0] -s*[1] s[2] -s*[3] … s[K-2]-s*[K-1])T和S2=(s[1] +s*[0] s[3] +s*[2] … s[K-1] +s*[K-2])T。S1,S2分别进行反傅里叶变换(Inverse Fast Fourier Transformation,IFFT)并添加循环前缀,产生分组块X1,X2,…,XnT由各个相应的发射天线发射出去。
本文采用与文献4相同的假定:(1)OFDM符号的保护时间间隔大于多径信道的时延;(2)衰落信道满足准静态条件,即在每个OFDM符号期间信道参数保持不变,在不同的OFDM符号持续期间信道参数可独立随机变化;(3)不同收发天线对之间的信道相互独立,且第i个发射天线到第个接收天线之间的信道冲激响应可建模为L抽头的有限脉冲响应滤波器,即(t)δ(t-τm(t)),αm,j,i(t)为抽头系数,τm(t)是第m条路径的时延,αm,j,i(t)是均值为0、方差为1/L的复高斯随机过程;(4)每个子带的各个相邻子载波的信道增益近似相等;(5)接收机理想同步。


2 矩形MQAM的误码性能分析
考虑由相互独立的同相M1进制脉冲幅度调制(Pulse Amplitude Modulation,-PAM)信号和正交MQ-PAM信号构成的矩形MQAM信号,M=M1MQ,并假定接收机采用匹配滤波器和相干检测,则加性高斯白噪声信道上矩形MQAM的误符号率(Symbol Error Rate,SER)为[5]:

式中,a1=0,η=dQ/d1是正交与同相判决距离比。
式4对式2求统计平均可得有信道估计误差的矩形MQAM调制SFBC-OFDM系统的平均SER为:
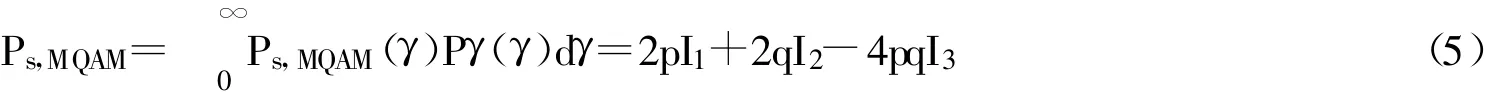
利用高斯Q函数的另一种数学表达式[7,8]Q(x)=Q(y)=[1/(2π)](2sin2θ))dθ,并采用矩生成函数方法,由式4,5经推导可得:

将式3的矩生成函数代入式6,并进行变量代换x=cos2θ,经推导得:
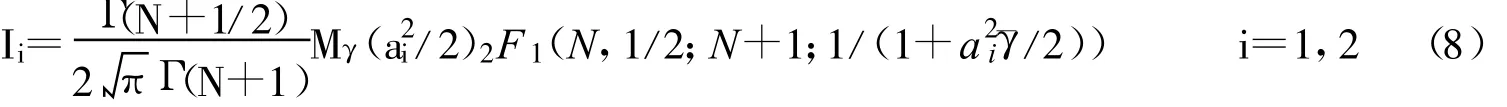
式中,2F1(a;b;c;z)为高斯超几何函数,其定义为:
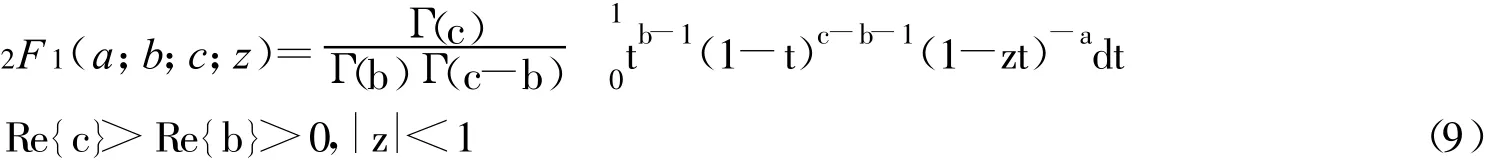
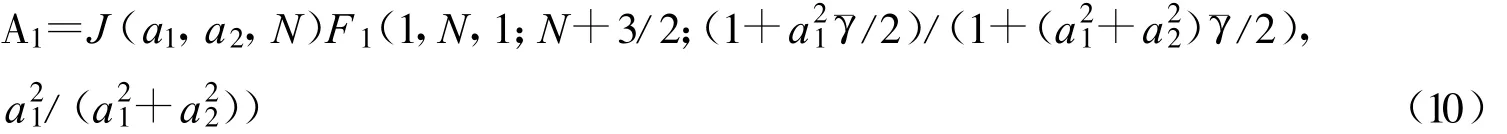
对A1进行变量代换x=1-()tan2θ,可推得 :
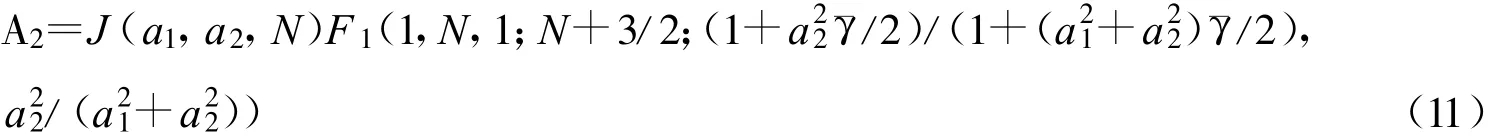
式中,F1(a,b1,b2;c;z1,z2)为Apell超几何函数,其定义为:
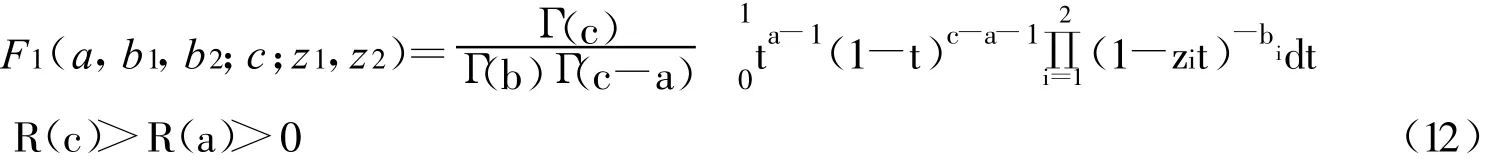
将式8,10,11代入式5,可得瑞利衰落信道上有信道估计误差的矩形MQAM调制SFBC-OFDM系统的平均SER精确解析表达式。
3 矩形MQAM的近似误码性能分析
利用高斯Q函数的指数近似表达式[9]Q(x)=(e-x2/2/3+e-2x2/3)/4,将其代入式4并利用矩生成函数方法,可推得瑞利衰落信道上有信道估计误差的矩形MQAM调制SFBC-OFDM系统平均SER的近似表达式为:

4 数值计算结果
本文以矩形8×4QAM、16×8QAM和G2编码方式为例对瑞利衰落信道上有信道估计误差的SFBCOFDM系统在不同的接收天线数、不同的η和值下的平均SER性能进行了数值计算,结果如图2、3所示。当矩形MQAM信号的同相分量与正交分量的平均能量相等时,对于16×8QAM,有η=由图2可知,增加接收天线数能够显著改善SFBC-OFDM系统的平均SER性能。由图3可知,随着η的增大,(nT,nR)=(2,3)的SFBC-OFDM系统的平均SER性能会变差。同时我们亦注意到,由式13所得的近似SER与式5的精确SER非常接近;信道估计误差会恶化SFBC-OFDM系统的平均SER性能;随着的增大,SFBC-OFDM系统的平均SER性能会变差;当为固定值时,SFBC-OFDM系统的平均SER性能会出现一个差错平台。
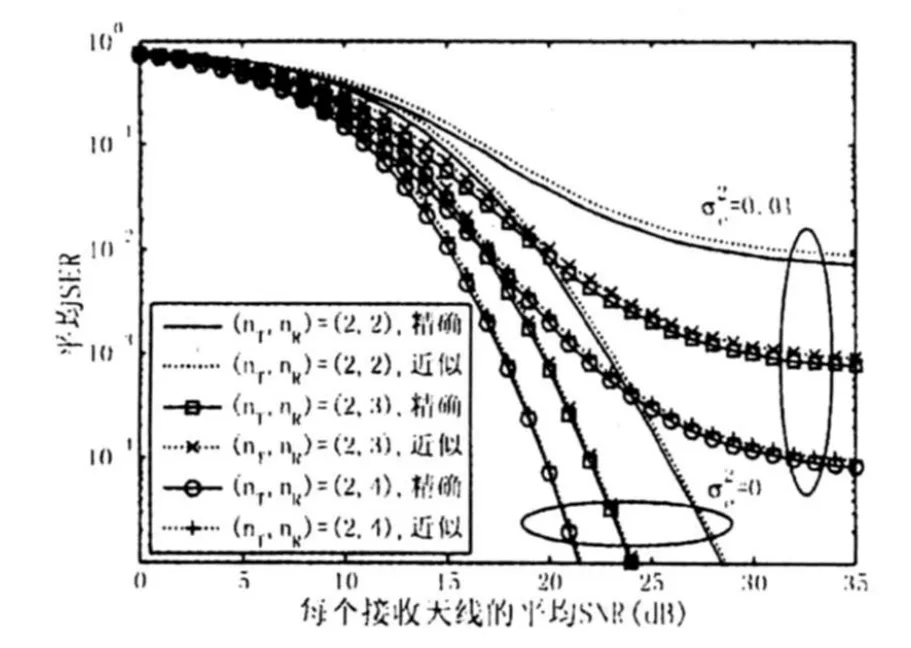
图2 矩形8×4QAM的平均SER性能(η=1)
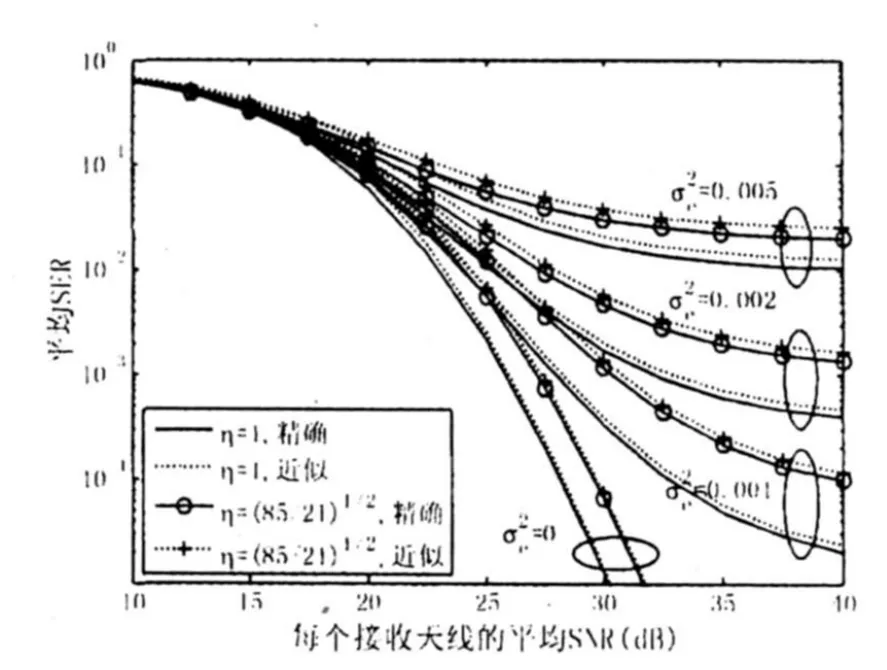
图3 矩形16×8QAM的平均SER性能
5 结 论
本文使用MGF方法和高斯Q函数的指数近似表达式推导了MIMO衰落信道上有信道估计误差的矩形MQAM调制SFBC-OFDM系统平均SER的精确和近似解析表达式。本文的结果为MIMO衰落信道上采用SFBC-OFDM的矩形MQAM数字调制系统设计提供了一种方便、快捷的理论分析工具,避免了耗时的计算机仿真。
[1] Lee K F,William sD B.A space-frequency transmitter diversity technique for OFDM systems[C].San Francisco:Proc of IEEE Globecom,2000:1 473-1 477.
[2] Li L,Tao X,Zhang P,et al.A practical space-frequency b lock coded OFDM scheme for fast fading broadband channels[C].Lisbon:Proc of IEEE Pimrc,2002:212-216.
[3] Torabi M,Soleymani M R.Performance evaluation of space-frequency coded OFDM systems over frequency selective fading channels[C].Montreal:Proc of IEEE Ccece,2003:1 699-1 702.
[4] Torabi M,A?ssa S,Soleymani M R.On the BER Performance of Space-Frequency Block Coded OFDM Systems in Fading MIMO Channels[J].IEEE Trans Wireless Commun,2007,6(4):1 366-1 373.
[5] Lei X,Fan P,Hao L.Exact symbol error probability of general order rectangular QAM with MRC diversity reception over Nakagami-mfading channels[J].IEEE Commun Lett,2007,11(12):958-960.
[6] Tarokh V,Jafarkhani H,Chalderbank A R.Space-time block coding for wireless communications:performance results[J].IEEE Trans Sel Areas Commun,1999,17(3):451-460.
[7] Craig JW.A new,simple and exact result for calculating the probability of error for two-dimensional signal constellations[C].Mclean:Proc of IEEEMilcom,1991:571-575.
[8] Li R,Kam PY.Averages of the product of two Gaussian Q-function over fading statistics and applications[J].IEEE Commun Lett,2007,11(1):58-60.
[9] ChianiM,Dardari D,Simon M K.New exponential bounds and approximations for the computation of error probability in fading channels[J].IEEE Trans Wireless Commun,2003,2(4):840-845.
