含右删失数据的随机效应模型的统计分析
2010-11-26金晶亮
金晶亮
(南通大学,江苏南通226007)
0 引 言
在复杂系统中,具有很多不确定性的因素,建立数学模型时经常需使用概率统计模型。一方面,随着回归分析理论的不断发展,随机效应模型已成为目前重要的研究课题;另一方面,数据一般含有删失或不精密的特点。删失分为“右删失”和“左删失”,个体的确切寿命不知道,只知道寿命大于L,则称该个体的寿命在L是右删失的,并说L是右删失数据[1]。由于删失的引入,情况大为复杂。普通的统计学未讨论这些,它只是讨论每个数据都是完全数据的情形。生存分析的一大特点,就是讨论含删失数据的情形,因而发展出许多新的统计方法。综合上述两方面,显然对既有随机效应又有删失数据的研究也是十分必要的。基于实际问题和理论研究的需要,本文主要研究既有随机效应又有删失数据的模型,侧重于统计诊断技术的研究。
1 含右删失数据的非线性随机效应模型
假设Y是一个(n+m)维的响应向量,u是q维的随机效应因子,假设u服从正态分布N(0,σ2Iq),Y1|u,Y2|u,…Yn+m|u,相互独立,且服从正态分布 N(μi,σ2),不失一般性,考虑最后 m 个生命时间数据由于试验的终止却未寿终而删失了。Yi|u在随机效应下的均值为:μi=(fxi,β)+u(i=1,2,…,n+m),其中β是p×1未知固定效应向量,令φ(y)=,联合似然函数方程由下式给出:L},对数似然函数可以写成:l(β,σ2,u)=-uTu,此处方程对β求导,可得),其中,wi具有右删失数据的原随机效应模型Y=(fX,β)+Zu+ε化为一般随机效应模型:
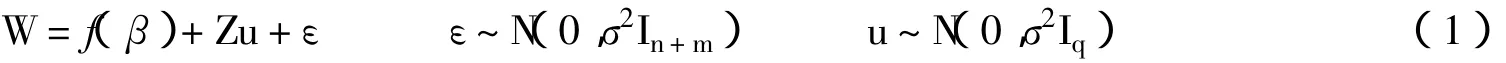

故式1可以改写为W=f(β)+e,e~N(0,σ2)。由此可看出,W关于(β,σ2)的对数似然为式2前3项,因此lp(β)作为正态的非线性随机效应模型的边缘似然是精确的(即Op(n-1)=0),Laplace的展开对于正态非线性随机效应模型是精确的。
1.1 模型的参数估计
介绍了含右删失数据的非线性随机效应模型,讨论参数β的估计方法及有关性质。
引理1对于正态非线性随机效应模型1,似然函数lp(β)关于参数β的Score函数与观察信息阵分别是][G],其中为方程∂l(W,u;β)/∂u=0的解,=(β),G=∂2f(β)/∂β∂βT-∂2W/∂β∂βT为 n× p× p立体阵,Ω=方括号乘积[·][·][2]。
证明式2对β求导得,-ip(β)T)-1代入即得结论。
1.2 算法
根据引理1,β的参数估计可采用通常的迭代算法,具体的算法如下:
(1)首先给出参数β的初值。这可采用不带随机效应的一般指数族非线性回归模型的常用算法[3,4],得到参数β的估计并取为初值β0,并取u0=ZT(Y-μ)|;(2)根据迭代计算出的βi,ui,给出Wi,;(3)给定参数β,解方程∂(lW,u;β)/∂u=0,即采用下列迭代公式:ui+1=(;(4)对于给定的u,解方程∂l(W,u;β)/∂β=0,求解参数β,这时可采用Gauss-Newton迭代法[5]。由于:ip(β),以φDTΩ-1D代替-¨lp(β),则Gauss-Newton迭代公式为若|βi+1-βi|与|ui+1-ui|均小于给定的精度,则停止迭代,否则重复上述步骤2-4,直至达到给定的精度。
2 含右删失数据的线性随机效应模型
2.1 模型的参数估计
假设Y是一个(n+m)维的响应向量,u是q维的随机效应因子,假设 u服从正态分布N(0,σ2uIq),Y1|u,Y2|u,…,Yn+m|u相互独立,且服从正态分布N(μi,σ2ε),不失一般性,考虑最后m个生命时间数据由于试验的终止却未寿终而删失了。Yi|u在随机效应下的均值为:μi=xTiβ+ziTu(i=1,2,…,n+m),其中β是p×1未知固定效应向量令φ(y联合似然函数为:L=},记λ0=对数似然函数为:

2.2 实例分析
某产品的使用寿命与温度T的高低有关,数据来自加速寿命试验如表1所示(数据来源:文献1)。根据同类产品的知识,寿命时间t与绝对温度T之间应有关系式

表1 加速寿命试验数据(栏目中“1”表示寿终,“0”表示未寿终)
由于试验数据是重复测量的,可以考虑随机效应模型:Yij=μi+αj+eij,i=1,2,3,4,j=1,2,3,4,其中μi是固定效应,α1,α2,α3,α4为随机效应,假定αj,eij都互不相关,且E(αj)=0 Var(αj)=,Var(eij)=。利用前面介绍的算法,可以得到估计值根据前面讨论的统计诊断量进行计算,得到如下结果如表2所示:显示10号,12号,16号是强影响点。
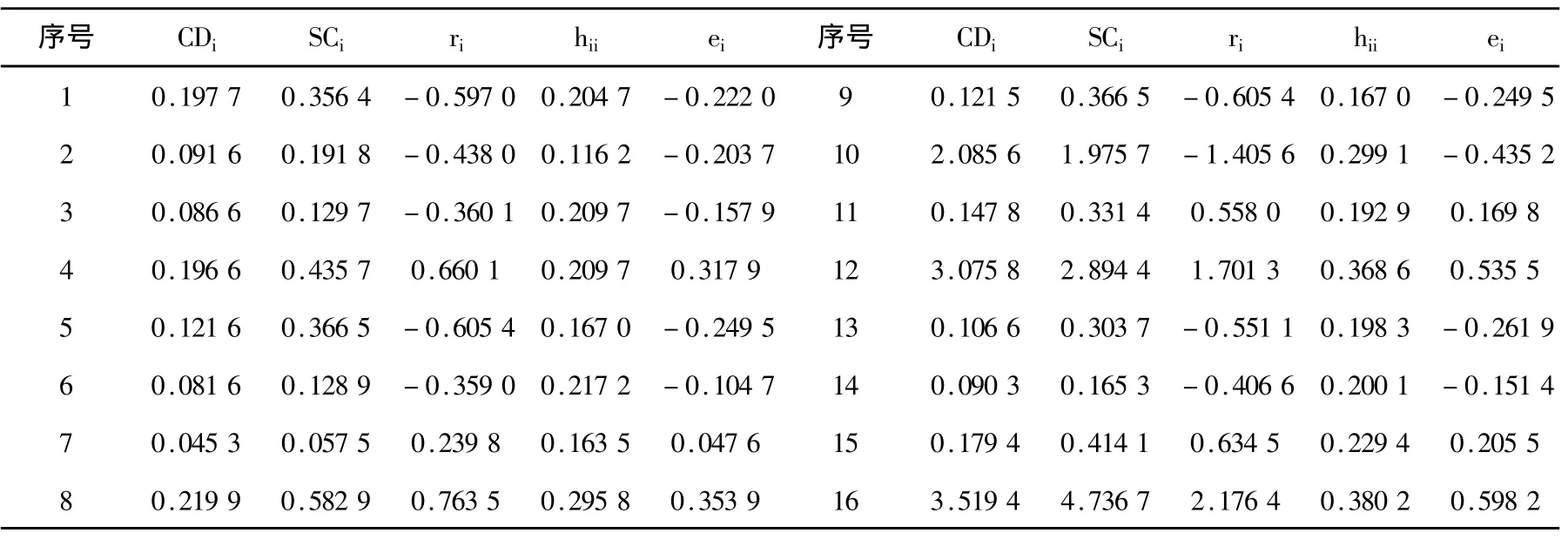
表2 加速寿命试验诊断统计量(min)
[1] 彭非,王伟.生存分析[M].北京:中国人民大学出版社,2004:197.
[2] 王松桂.线性模型理论[M].北京:科学出版社,2004:17-43.
[3] Wei BC.Exponential Family Nonlinear Models[M].Singapore:Springer-Verlag,1998:215-228.
[4] Wei B C.On confidence regions of embedded models in regular parametric families(A geometric approach)[J].Austral:J Statist,1994,36(2):327-328.
[5] 韦博成,鲁国斌,史建清,等.统计诊断引论[M].南京:东南大学出版社,1991:23-56.
