闭合旋转薄壳的非线性模态方程*

孟庆照, 李小菊, 张志良

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

闭合旋转薄壳的非线性模态方程*

孟庆照, 李小菊, 张志良

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

采用Sanders薄壳理论和虚功原理推导了闭合旋转薄壳的几何非线性模态方程,其系数计算公式适合于用数值方法确定.用已有理论和解析结果证实了本文工作的正确性.Donnell非线性浅壳理论所得到的平方非线性的系数值与本文结果基本相同,而立方非线性的系数值则比本文结果明显偏小.

旋转薄壳；非线性；模态方程;Sanders薄壳理论；离散

0 引 言

薄壳结构在航空、航天、船舶、建筑、核能等工业领域应用广泛,非线性振动将破坏其稳定性.直接采用有限元等数值方法计算薄壳非线性振动的时间历程不仅计算成本高,而且海量般多次迭代运算存在可靠性问题.因此,将薄壳正确离散为有限个自由度系统是分析研究薄壳非线性振动的关键.在此过程中，通常采用线性模态的叠加离散连续系统[1-3].对存在几何非线性任意形状的弹性薄壳,Radwan等[1]离散给出了有限自由度非线性模态振动方程,但方程过于复杂,且不适合于数值计算,因此，它的应用受到限制.即使在圆柱壳这种形状最为简单的旋转薄壳的离散中,也不直接采用文献[1]的结果,而是通过Galerkin 方法[2]、Lagrangian方程等[3]得到有限自由度的非线性振动方程.本文推导具有几何非线性的闭合旋转薄壳的非线性模态方程,利用周向三角函数解的正交性,得到了较为简单的结果,并给出了方程中系数的有限元数值计算公式.最后,利用已有理论和解析结果证实了本文结果的正确性.

1 非线性模态方程

对存在几何非线性的旋转闭合薄壳,其应变势能含有3次和4次项,即

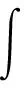
式(1)中:r,θ分别为柱坐标系中的径向坐标和角坐标;s为薄壳母线坐标;q代表薄壳的3个位移分量;下标代表q的幂次.

由虚功原理可写出弹性薄壳的非线性运动方程[4]

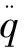
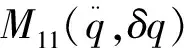
式(3)中,h为薄壳厚度.可见,对旋转闭合薄壳,方程(2)的各函数具有相同的积分形式.

将q展开为线性模态的叠加,对旋转薄壳,模态的周向解是三角函数.为方便以下运算,采用复指数函数的形式,即

式(5)中:c.c.代表其前边项的共轭复数;g为任意正整数,根据实际问题确定.模态yn(s,θ)=Yn(s)einθ,且有以下关系:

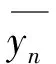
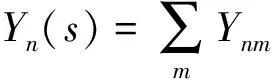
将式(5)代入运动方程(2)的前2项,得

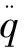
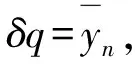
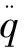
式(8)中:ωn为与模态yn对应的固有频率;质量mn为

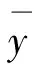
为得到P21(q,δq)的模态表达式,首先由式(5)得

因而有

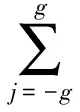
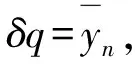
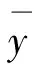
经过与前述相同的推导,得到立方非线性的模态表达式

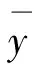
式(13)中的P211和P1111项分别为应变能P4(q)的二阶和三阶变分.

将式(8)、式(12)和式(13)代入方程(2),得到离散化的旋转闭合薄壳非线性模态方程

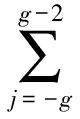
可见,方程中出现了2次和3次非线性项,除模态自身的非线性项外,还出现了模态间的非线性耦合项.

2 方程系数的确定

仅当简单支撑边界条件下的圆柱壳,方程的系数可以解析求得，对一般形状的旋转薄壳,这些系数必须借助数值方法得到,笔者采用的是有限元方法和Sanders薄壳理论[4].据Sanders理论,式(1)中的应变能密度分别为:

式(15)～式(17)中：伸长劲度K=Eh(1-v2);线性应变分量εs,εθ,εsθ,κs,κθ和κsθ以及角位移βs,βθ和β与位移的关系见文献[4].

据位移分量的相位关系,线性模态yn表示为

类似地,

位移U(n)和节点广义位移y(n)关系由有限元中的形函数矩阵N表出:

据式(5),虚位移δq可表示为

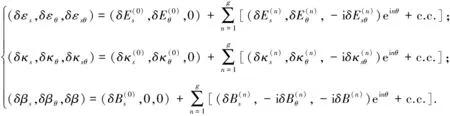
(23)

据标准的有限元方法得线性本征值问题

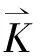
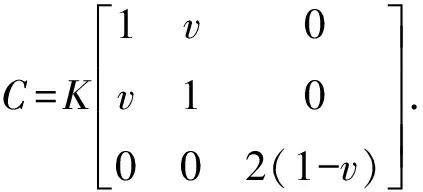
(25)

求得本征值后,据式(9)可算得质量mn.

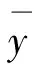
式(28)中:k=n-j;列矩阵ξ和η的分量为

式(29)中的v1=1-v.虽然由对式(12)的讨论知,总有j≥1,但是为了保持公式的普适性，式(29)中引入符号函数s(j),以对

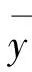
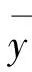
式(31)中:l=n-j-k;列矩阵λ的分量为

式(32)中:v2=1+v;另外2个三次非线性项的系数由变分规则直接据下式计算:

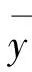
至此,非线性模态方程(14)的系数计算公式已全部给出.首先由式(24)计算线性固有频率和模态,然后由式(8)计算线性项系数,最后根据式(28)、式(30)、式(31)和式(33)计算非线性项系数,式(28)和式(33)中诸量通过式(20)和式(21)由已知的线性模态位移计算.

3 应用和验证例

文献[2]研究了两端为简单支撑的圆柱壳受横向激励的非线性振动,其激励为

式(34)中:ξ=s/L;L为圆柱壳长度.其选用的模态为

式(35)中的横向位移w前的负号是由于文献[2]的w以内法线为正方向,与本文相反.注意该文为了研究轴对称模态对薄壳非线性振动类型(硬弹簧还是软弹簧)的贡献选用了3个轴对称模态,因此,本文给出的模态展开式(5)和非线性模态方程(14)必须稍作推广.考虑到最后一个轴对称模态基本无贡献[2],且又不失一般性,以下推导中不计该模态.对于2个轴对称模态,按如下2步列写方程:首先仅考虑1个轴对称模态α0y0和非轴对称模态,按方程(14)写出方程;然后,按代数运算法则对所得方程作如下替换:

得

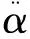
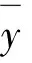
(37)

另一个轴对称模态方程与上式相似,这里不列出.可以看到,同一个模态方程中各项α的下标值之和相同,对非轴对称模态方程(37),该和值为n;对轴对称模态方程,该和值为0.或者说,每个模态方程含有的项为所有模态乘积的排列组合,该组合的α的下标值之和等于模态的周向波数.注意到这点,并注意α的排列组合和前面系数的对应关系,对模态不多的系统,方程可容易写出.

利用α0=c0和αn=(cn-idn)/2,将方程(37)和(38)转换为实系数方程

式(39)和式(40)中：上标撇代表对归一化时间τ=ωnt求导;幅度则由薄壳厚度h归一化,

文献[2]所研究的圆柱壳的几何参数为长0.2 m,半径0.1 m,厚度0.247 mm;材料参数为E=7.102×1010N/m,v=0.31,ρ=2 796 kg/m3，非轴对称模态的周向波数n=6.表1比较了本文和文献[2]列出的结果.由表1可知，除系数h6外,其余结果差别不大.差别的原因应该是本文采用了较为精确的Sanders薄壳理论,而文献[2]则采用了较为近似的Donnell浅壳理论.但系数h6如此大的差别,应对此作进一步考察.

表1 本文和文献[2]的系数值比较

首先证实本文系数值h6的有效性.在式(17)中仅考虑β4θ,并且在动能和势能中忽略面内惯性和面内应变,由文献[1]中的式(50)得

代入具体数据算得h6=0.498,与本文数据较为接近,这证实了本文结果的正确性.

鉴于许多作者采用Donnell非线性浅壳理论,有必要考察文献[2]的h6值为何显著偏低.当周向波数较大时,由采用相同理论的文献[5]在附录B所给出的公式可以推得h6的计算式为

由式(43)算得h6=0.300,与文献[2]结果相同.比较式(42)和式(43),看到两者相差因子3/[2(1-v2)],约为1.6,大致为本文结果和文献[2]结果的倍数.Donnell浅壳理论的近似性主要是忽略了面内惯性以及转角中的面内位移分量,在求解von Karman形式的运动方程中,面内边界条件和周向位移的连续性仅满足积分.对目前周向波数较大,且振型以w为主的模态,忽略面内惯性和面内位移分量应不至于引起如此大的差异.这种差异极可能是由于面内边界条件和周向位移的连续性仅满足积分而造成的.

文献[3]比较了Donnell,Sanders,Flügge,Novozhilov 4种薄壳理论和Donnell浅壳理论在圆柱壳非线性固有频率漂移的结果.前4种理论采用Lagrangian方法,而Donnell浅壳理论采用求解von Karman形式运动方程.发现5种理论虽然都导致薄壳非线性的软弹簧特性,但由Donnell浅壳理论所得到的结果明显过软,其他4种理论的结果基本相近.文献[3]将其归因于Donnell浅壳理论忽略了面内惯性,从而导致线性轴对称模态固有频率的差异.现在看到Donnell浅壳理论得到明显过软的结果应是由于其立方非线性项的系数值显著偏低引起,而这种相比于其他理论结果明显过软的事实进一步证实了本文结果的正确性.

4 结 论

推导了闭合旋转薄壳的非线性模态方程,其系数计算采用Sanders薄壳理论.给出的系数计算公式适宜于数值编程实现.所得方程可用于研究一般形状旋转薄壳在任意边界条件下的静态或动态非线性响应.已有结果和解析结果证实了本文工作的正确性.Donnell非线性浅壳理论所得到的平方非线性的系数值与本文结果基本相同,而立方非线性的系数则明显偏小.

[1]Radwan H,Genin J.Non-linear mode equations for thin elastic shells[J].Non-Linear Mechanics,1975,10:15-29.

[2]Amabili M,Pellicano F,Paidoussis M P.Non-linear dynamics and stability of circular cylindrical shells containing flowing fluid,Part II:large-amplitude vibrations without flow[J].J Sound Vib,1999,228(5):1103-1124.

[3]Amabili M.A comparison of shell theories for large-amplitude vibrations of circular cylindrical shells:Lagrangian approach[J].J Sound Vib,2003,264(5):1091-1125.

[4]Maewal A.Finite element analysis of steady nonlinear harmonic oscillations of axisymmetric shells[J].Computer methods in applied mechanics and engineering,1986,58(1):37-50.

[5]Kubenko V D,Kovalchuk P S,Kruk L A.Non-linear interaction of bending deformations of free-oscillating cylindrical shells[J].J Sound Vib,2003,265(2):245-268.

(责任编辑 杜利民)

Nonlinearmodalequationsforclosedrevolutionshells

MENG Qingzhao, LI Xiaoju, ZHANG Zhiliang

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

Nonlinear modal equations for closed revolution shells were derived according to the virtual work principle by the Sanders nonlinear shell theory. The coefficients of the equations were well-suited for numerical calculation. The obtained results were verified by the known published results. The coefficient values of the square terms derived from the Donnell′s nonlinear shallow-shell theory seemed very close to the present results, whereas the coefficient values of the cubic terms were significantly under-estimated.

revolution shell; nonlinear; modal equation； Sanders nonlinear shell theory; discretization

1001-5051(2010)01-0063-07

2009-11-04

浙江省自然科学基金资助项目(100039)

孟庆照(1976-),男,河南洛阳人,硕士研究生.研究方向:非线性振动.

张志良

O326

A