异常空心光束通过环形硬边光阑的传输特性

王奎龙

(杭州师范大学 基础医学部，浙江 杭州 310036)

在实际的光学系统中，光束的传输总要受到光阑的限制，因此对光阑限制下光束传输特性的研究是非常有意义的.文章对异常空心光束通过圆环形硬边光阑的传输特性进行分析，通过把环形光阑函数展开为复高斯函数的方法，推导出了异常空心光束通过环形光阑的传输近似公式，通过数值计算模拟对异常空心光束通过环形光阑的衍射特性进行研究，以期能为光束的整形提供一种简便的方法.

1 异常空心光束通过圆环形硬边光阑近轴ABCD系统后的场分布

在直角坐标下，z=0入射面处的异常空心光束的场分布可以描述为：

(1)

式中w0x和w0y分别表示像散高斯光束在x和y方向的束腰宽度[14].

若入射面是内半径为a、环宽为b的圆环形硬边光阑，圆环光阑的窗口函数表示为：

(2)

在近轴条件下，异常空心光束通过光阑近轴光学系统后出射场的分布可由直角坐标下的Collins积分公式得到：

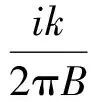
(3)

式中E(x1,y1,0)和E(x,y,z)分别表示入射面和出射面上光束的电场分布.k=2π/λ是波数，λ是波长，A、B、C和D是近轴光学系统的变换矩阵元.

将硬边光阑窗口函数拓展为一组复高斯函数之和：

(4)

式中An和Bn分别为拓展的复系数，可从计算机优化中得到.将式(1)和式(4)代入式(3)，经过复杂积分计算后，可以得到异常空心光束通过圆环形硬边光阑后出射面上的场分布的近似解析表达式：

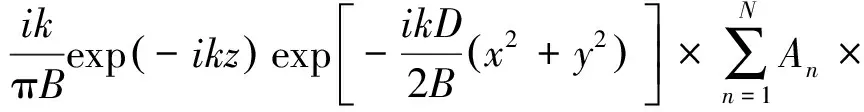
(5)

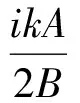
(6)

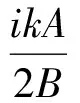
(7)

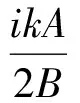
(8)

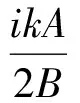
(9)

2 数值计算和分析

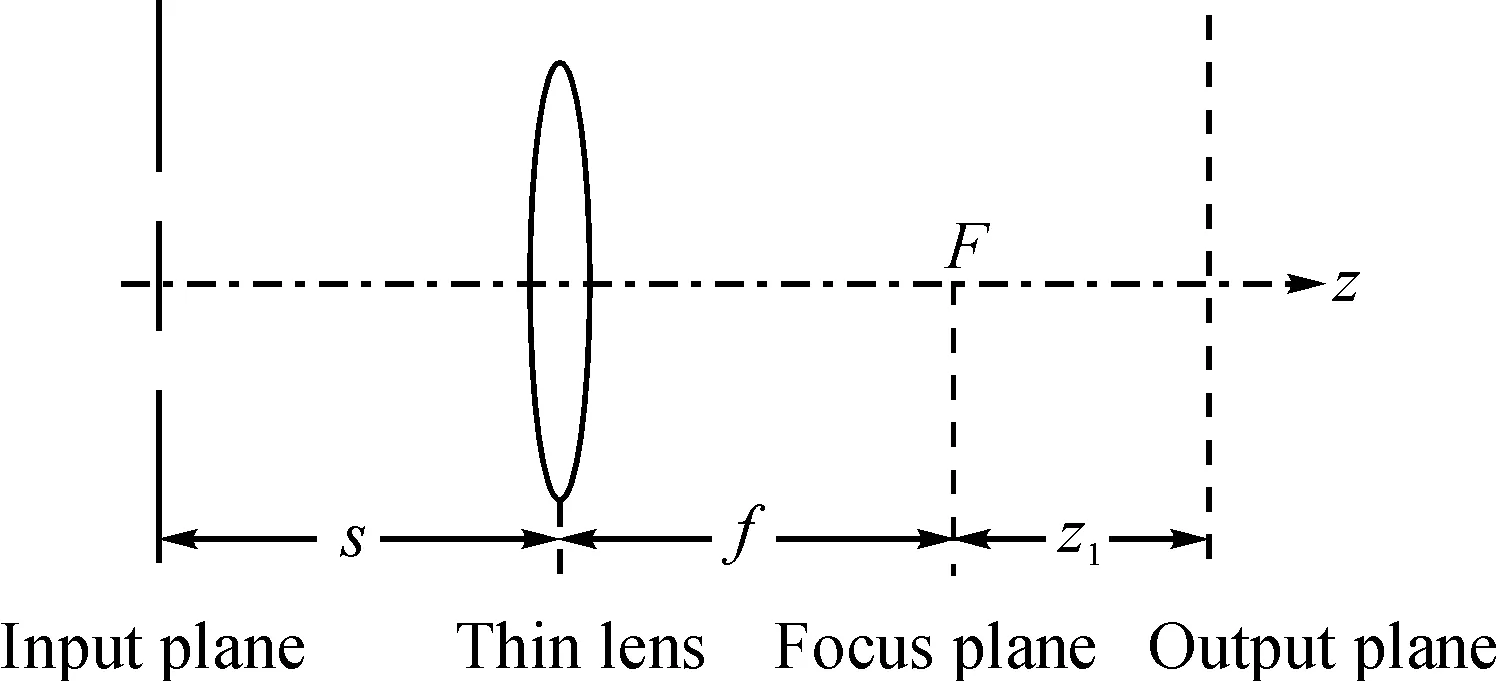
图1 异常空心光束通过环形光阑透镜系统的传输Fig. 1 Propagation of anomalous hollow beam passing an annular aperture-lens system

由式(5)可知，出射场分布与光阑宽度、光阑内外半径、光束束腰等参数密切相关.由该式同时可知，当取a=0，则为半径等于b的圆孔光阑衍射；当取a=0,b→∞，则为无光阑传输.在此考虑光束通过如图1所示的近轴光学系统，系统的变换矩阵为：

(10)

将A、B、D代入式(5)，在Mathematica环境下，对式(5)进行数值模拟，讨论焦平面上光强分布与光阑宽度、光阑内外半径的关系.在下面计算中，取w0x=1 mm,w0y=2 mm,λ=632.8 nm,f=500 mm,s=300 mm,An和Bn的取值见文献[15]中表1.

2.1 光强分布随光阑宽度变化情况

图2是a=0.5 mm,z1=0 mm，不同光阑宽度衍射时焦平面上的光强分布图.从图示情况可以看出，焦平面上的光强分布与光阑宽度密切相关.光阑环宽越小，光强分布范围越大，级次越多，即衍射效应越强，随着光阑宽度的增加，衍射逐渐减弱，光强分布逐渐集中.由于异常空心光束是椭圆对称光束，具有椭圆的实心内核和椭圆对称的外环，在圆环形光阑作用下，x方向和y方向具有不同的遮拦比，因此光阑对光束的x方向和y方向影响程度不同，体现出不同的衍射特征.随着光阑宽度的增加，y方向次级极大值逐渐减弱，而x方向次级极大值先是逐渐增强，再逐渐减弱.中心光强随着光阑宽度的增加体现先逐渐减弱为零再逐渐增强的特征，当环宽b=0.26 mm时，中心光强为零，而x方向和y方向各有两个极大值.当环宽大于3 mm后，衍射基本可以忽略，光强分布形状基本与无光阑时一样，只是光强较弱.

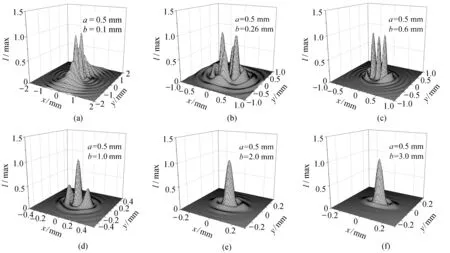
图2 异常空心光束通过宽度不同的环形光阑时焦平面上的归一化光强分布Fig. 2 Normalized intensity of anomalous hollow beam on the focusing plane after it passes through the annular apertures with different width and same inner radius

2.2 光强分布随光阑内径变化情况

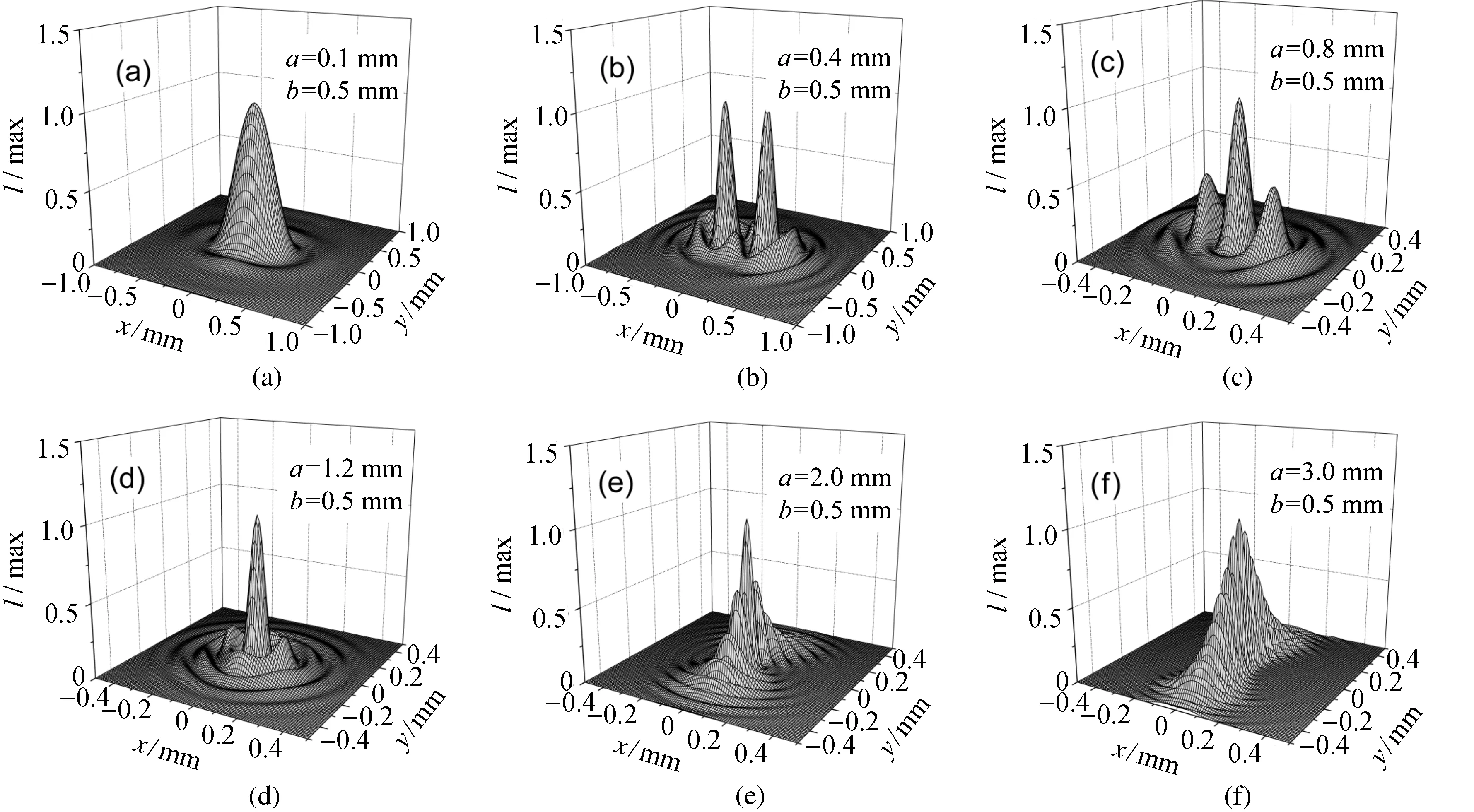
图3 异常空心光束通过内半径不同的环形光阑时焦平面上的归一化光强分布Fig. 3 Normalized intensity of anomalous hollow beam on the focusing plane after it passes through the annular apertures with different inner radius and same width

图3为光阑宽度b=0.5 mm，z1=0，内环半径不同时焦平面上的光强分布图.从图中可以看出，焦平面上的光强分布与内环半径的大小密切相关，同样x方向和y方向具有不同的衍射特征.当内环半径较小时，衍射效应较弱，随着内环半径的增加，x方向的衍射先是逐渐增强，再逐渐减弱，而y方向衍射逐渐增强，旁瓣不断增加，光束分布范围逐渐变大.

综合以上两种情况，焦平面上的光强衍射特性与环形光阑的宽度、光阑的内径等参数密切相关，当光阑的内径和光阑宽度取适中时，光束中心会出现1至4个光强相等的峰，或者中心光强为零的分布.因此，通过控制环形光阑参数，可以方便地实现光束的整形或控制.

3 结 论

文章采用把光阑函数展开为复高斯函数的技巧，用Collins公式推导出了异常空心光束通过圆环形硬边光阑的传输近似解析公式.利用导出的公式，数值研究了异常空心光束通过环形光阑透镜系统的传输特性.结果表明，焦平面光场分布与光阑内径、光阑宽度等参数有关.文章的结果对异常空心光束的应用和光学系统的设计有实际参考价值.

[1] Yin Jianping, Gao Weijian, Zhu Yifu. Generation of dark hollow beams and their applications[C]//Wolf E. Progress in Optics. North-Holland: Elsevier Science B.V.2003,45:119-204.

[2] Kuga T, Torii Y, Shiokawa N,etal. Novel optical trap of atoms with a doughnut beam[J]. Phys Rev Lett,1997,78(25):4713-4716.

[3] Ito H, Sakaki K, Jhe W,etal. Laser spectroscopy of atoms guided by evanescent waves in micron-sized hollow optical fibers[J]. Phys Rev Lett,1996,76(24):4500-4503.

[4] Yin Jianping, Zhu Yifu, Jhe W,etal. Atom guiding and cooling in a dark hollow laser beam[J]. Phys Rev A,1998,58(1):509-513.

[5] Wang Xiao, Littman M G. Laser cavity for generation of variable-radius rings of light[J]. Optics Lett,1993,18(10):767-768.

[6] Lee H S, Stewart B W, Choi K,etal. Holographic nondiverging hollow beam[J]. Phys Rev,1994,49(6):4922-4927.

[7] Yin Jianping, Noh H R, Lee K I,etal. Generation of a dark hollow beams by a small hollow fiber[J]. Opt Commun,1997,138(4):287-292.

[8] Balykin V I, Letokhov V S. The possibility of deep laser focusing of an atomic beam into the A-region[J]. Opt Commun,1987,64(2):151-156.

[9] Gori F, Guattari G, Padovani C. Bessel-Gaussian beams[J]. Opt Commun,1987,64(6):491-495.

[10] Lu Xuanhui, Chen Xumin, Zhang Lei,etal. High-order Bessel-Gaussian beams and its propagation properties[J]. Chin Phys Lett,2003,20(12):2155-2157.

[11] Cai Yangjian, Lu Xuanhui, Lin Qiang. Hollow Gaussian beams and their propagation properties[J]. Opt Lett,2003,28(13):1084-1086.

[12] Cai Yangjian, Lin Qiang. Hollow elliptical Gaussian beam and its propagation through aligned and misaligned paraxial optical systems[J]. J Opt Soc Am A,2004,21(6):1058-1065.

[13] Wu Y K, Li J, Wu J. Anomalous hollow electron beams in a storage ring[J]. Phys Rev Lett,2005,94(13):134802.

[14] Cai Yangjian. Model for an anomalous hollow beam and its paraxial propagation[J]. Opt Lett,2007,32(21):3179-3181.

[15] Wen J J, Breazeale M A. A diffraction beam field expressed as the superposition of Gaussian beams[J]. J Acoust Soc Am,1988,83(5):1752-1756.