特定数字集的非谱问题

仲 明

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)

1 简 介

设M∈Mn(Z)是一个扩张整矩阵(即M所有特征值的绝对值都大于1),D⊆Zn是基数为|D|的有限数字集.联系到自仿迭代函数系(IFS){Φd(x)=M-1(x+d)}d∈D,则存在唯一的概率测度μ:=μM,D满足等式

(1)

设S⊆Zn是和D具有相同基数的有限子集,联系到它的对偶迭代函数系(IFS){Ψs(x)=M*(x)+s}s∈S.令ΛM,S表示0关于迭代函数系{Ψs(x)}s∈S的轨道,即

(2)

其中M*是M的共轭转置.

回忆紧支撑在Rn上的自仿测度μ,如果存在一个离散的集合Λ使得EΛ:={e2πi〈λ,x〉:λ∈Λ}是L2(μ)空间的一个标准正交基,则称μ为谱测度,Λ称为谱测度μ的谱,(μ,Λ)为谱对.谱测度是由Fuglede[1]的一个著名猜测所引起的谱集的自然推广.

假设存在集合ΛM,S⊆Rn,ΛM,S-ΛM,S⊆Rn使得EΛM,S在L2(μM,D)空间中正交,则对任意λ1≠λ2∈ΛM,S,

(3)

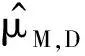
(4)

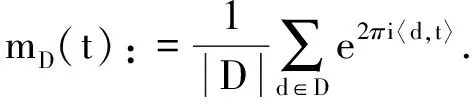
将式(3)和(4)结合,则存在一个正整数k=k(λ1-λ2)使得mD(M*-kλ)=0,其中

λ=λ1-λ2∈Zn{0}.

目前,谱自仿测度问题的研究主要是两个方面:一方面,在什么条件下μM,D是一个谱测度,相关的结果见[2,3];另一方面是关于μM,D不是谱测度的条件的研究,相关内容见[4-5].前辈们的研究得到了许多结果[1-5].这些结果中数字集D中的向量大多是线性无关的,但是如果数字集中的向量发生变化,如线性相关,那么又会出现什么样的结论?这问题来自文献[5]的一个猜测(Conjecture 1),但其只说明了数字集的个数,并没有要求数字集的具体形式.事实上,可以证明下面两个定理.

定理1若|pi|>1,pi∈2Z+1(i=1,2,3).联系到整数矩阵和数字集

(5)

的自仿测度μM,D是非谱测度.则在L2(μM,D)空间中至多存在4个相互正交指数函数且4是最好估计.

定理2若|pi|>1(i=1,2),p1,p2,p∈Z,p1p2∉3Z,l∈Z{0,1}.联系到整数矩阵和数字集

(6)

的自仿测度μM,D是非谱测度.则如果l∈3Z+2,则在L2(μM,D)空间中至多存在3个相互正交指数函数且3是最好估计;如果l∉3Z+2,则在L2(μM,D)空间中至多存在1个μM,D-正交指数函数.

2 定理1的证明

证明如果在L2(μM,D)空间中存在5个正交指数函数,设它们是e2πi〈λ1,x〉,e2πi〈λ2,x〉,e2πi〈λ3,x〉,e2πi〈λ4,x〉,e2πi〈λ5,x〉，其中λi=(λi1,λi2,λi3)T(i=1,2,3,4,5)∈R3.那么,

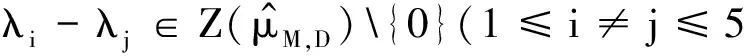
(7)

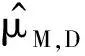
首先,对于在式(5)中给定的D有：

Θ0:={t∈R3:mD(t)=0}=A1∪A2,

其中

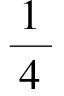
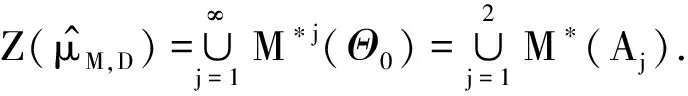
(8)

式中

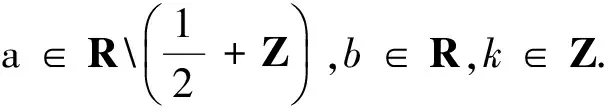
引理1上面所给的集合Z1,Z2,Z3有如下的性质:

(a)Z1,Z2,Z3互不相交的;

(c)Zj=-Zj,j=1,2,3;

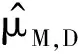
由式(7)和式(8),有

属于这3个集合(Z1,Z2,Z3)的并.特别的,

λ1-λ2,λ1-λ3,λ1-λ4,λ1-λ5∈Z1∪Z2∪Z3.

(9)

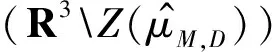
情况1集合Z2包含式(9)中一个差式.不妨设λ1-λ2∈Z2,故

λ1-λ3,λ1-λ4,λ1-λ5∈Z1∪Z3.

(10)

于是又可以将证明分为两种情况.

1) (3-0)(或者0-3)形式.即式(10)中的3个差式或者属于Z1或者属于Z3.

在这种情况下,若λ1-λ3,λ1-λ4,λ1-λ5∈Z1,那么,

λ4-λ3=(λ1-λ3)-(λ1-λ4)∈Z1-Z1;
λ5-λ3=(λ1-λ3)-(λ1-λ5)∈Z1-Z1;
λ5-λ4=(λ1-λ4)-(λ1-λ5)∈Z1-Z1.

由式(7)和引理1(d)知

λ4-λ3,λ5-λ3,λ5-λ4∈Z3.

由上式知

λ5-λ4=(λ5-λ3)-(λ4-λ3)∈Z3-Z3.

由式(7)和引理1(d)知,λ5-λ4∈Z1,这是一个矛盾.故这是不可能的.

若λ1-λ3,λ1-λ4,λ1-λ5∈Z3.同理可以得到矛盾.所以1)是不可能的.

2) (2-1)(或者1-2)形式.即Z1或Z3包含了式(10)中的任意两个差式,另外一个则包含了剩下的一个差式.

在这种情况下,如果λ1-λ3,λ1-λ4∈Z1,λ1-λ5∈Z3，那么,

λ4-λ3=(λ1-λ3)-(λ1-λ4)∈Z1-Z1;
λ2-λ3=(λ1-λ3)-(λ1-λ2)∈Z1-Z2;
λ2-λ4=(λ1-λ4)-(λ1-λ2)∈Z1-Z2.

由式(7)和引理1(d)知

λ4-λ3,λ2-λ3,λ2-λ4∈Z3.

由上式知

λ4-λ3=(λ2-λ3)-(λ2-λ4)∈Z3-Z3.

由式(7)和引理1(d)知λ4-λ3∈Z1,这是一个矛盾.故这是不可能的.其它情况可以类似得到矛盾.所以2)是不可能的.因此情况1是不可能的.

情况2集合Z2不包含式(9)中任意一个差式.即

λ1-λ2,λ1-λ3,λ1-λ4,λ1-λ5∈Z1∪Z3.

(11)

于是证明可以分为以下3种情况.

3) (4-0)(或者0-4)形式.这与情况1中1)类似.

4) (3-1)(或者1-3)形式.这也与情况1中1)类似.

5) (2-2)形式.即集合Z1和Z3都包含了式(11)中的任意两个差式.

在这种情形下,假设λ1-λ2,λ1-λ3∈Z1,λ1-λ4,λ1-λ5∈Z3,于是有

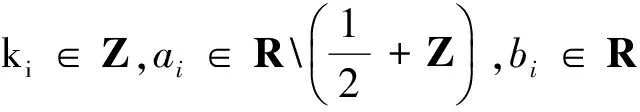
由式(7)和引理1(d)知

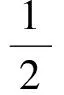
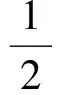
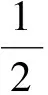
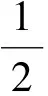
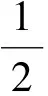
所以μM,D正交指数函数构成的任意集合最多有4个元素.进一步地,可以得到许多包含4个正交指数函数的集合.如指数函数系EΛ就是在L2(μM,D)空间中含有4个相互正交的指数函数集,其中

这就证明了4是最好估计.定理证毕.

3 定理2的证明

证明若l∈3Z+2.如果在L2(μM,D)空间中存在4个正交指数函数,设它们是e2πi〈λ1,x〉,e2πi〈λ2,x〉,e2πi〈λ3,x〉,e2πi〈λ4,x〉,其中λi=(λi1,λi2)T(i=1,2,3,4)∈R2.那么,

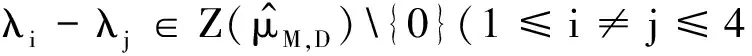
(12)

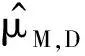
首先,对于在式(6)中给定的D有:

Θ0:={t∈R2:mD(t)=0}=A1∪A2,

其中

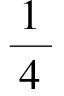
可以证明下式对于j=1,2,…都成立：M*j(Ai)⊆M*(Ai),i=1,2.所以,

(13)

式中

其中a∈R,k∈Z.显然,

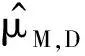
(14)

于是,由式(12)和(13),有

属于集合(Z1,Z2)的并.特别地,

λ1-λ2,λ1-λ3,λ1-λ4∈Z1∪Z2.

(15)

由式(14)知,这是不可能的.所以在L2(μM,D)空间中至多存在3个相互正交指数函数.进一步地,可以得到许多包含4个正交指数函数的集合.如指数函数系EΛ就是在L2(μM,D)空间中含有3个相互正交的指数函数集,其中

这就证明了3是最好估计.

若l∉3Z+2，则对于任意的ξ∈R2,有mD(ξ)≠0.这就证明了对于任意的扩张矩阵M∈Mn(R),μM,D是非谱测度,且在L2(μM,D)空间中至多存在1个μM,D正交指数函数.定理证毕.

[1] Fuglede B. Commuting self-adjoint partial differential operators and a group theoretic problem[J]. J Funct Anal,1974,16:101-121.

[2] Jorgensen P E T, Pedersen S. Dense analytic subspaces in fractalL2-spaces[J]. J Anal Math,1998,75(1):185-228.

[3] Laba I, Wang Yang. On spectral Cantor measures[J]. J Funct Anal,2002,193:409-420.

[4] Li Jianlin. Non-spectrality of plannar self-affine measures with three-elements digit set[J]. J Funct Anal,2009,257:537-552.

[5] Li Jianlin. The cardinality of certainμM,D-orthogonal exponentials[J]. J Math Anal Appl,2010,362:514-522.