7150铝合金高温热压缩变形流变应力行为

寇琳媛，金能萍，张 辉，韩 逸，吴文祥，李落星

(1. 湖南大学 材料科学与工程学院，长沙 410082；2. 苏州有色金属研究院有限公司，苏州 215026)

7150铝合金高温热压缩变形流变应力行为

寇琳媛1，金能萍1，张 辉1，韩 逸2，吴文祥2，李落星1

(1. 湖南大学 材料科学与工程学院，长沙 410082；2. 苏州有色金属研究院有限公司，苏州 215026)

在Gleeble-1500热模拟机上对7150铝合金进行高温热压缩实验，研究该合金在变形温度为300~450 ℃和应变速率为 0.01~10 s-1条件下的流变应力行为。结果表明：流变应力在变形初期随着应变的增加而增大，出现峰值后逐渐趋于平稳；峰值应力随着温度的升高而减小，随着应变速率的增大而增大；可用包含Zener-Hollomon参数的Arrhenius双曲正弦关系来描述合金的热流变行为，其变形激活能为226.698 8 kJ/mol；随着温度的升高和应变速率的降低，合金中拉长的晶粒发生粗化，亚晶尺寸增大，再结晶晶粒在晶界交叉处出现并且晶粒数量逐渐增加；合金热压缩变形的主要软化机制由动态回复逐步转变为动态再结晶。

7150铝合金；热压缩变形；流变应力；变形激活能；动态再结晶

7150铝合金属于Al-Zn-Mg系铝合金，具有高强度、高断裂韧性以及耐应力腐蚀等特点，广泛应用与航天领域[1-4]。通过增加 Zn、Mg、Cu等合金元素的含量，增加材料中的沉淀相，可以提高合金的强度，但同时会导致合金热加工性能降低。热加工性能是指材料在一定变形温度和应变速率下，得到预期的微观组织而不开裂所能承受的最大变形量。流变应力是表征金属和合金塑性变形性能的一个基本量，合金的流变应力值不仅决定了变形时所需施加的载荷的大小和所需消耗能量的多少，而且反映了合金热变形组织演化规律，并对材料的热加工性能直接影响。HU等[5-6]用热拉伸方法研究了 7050铝合金的高温流变应力行为，得到7050铝合金的热变形激活能为256.6 kJ，变形过程中的软化机制随Z值降低由动态回复转变为动态再结晶。LIN等[7]对Al-Zn-Mg-Cu铝合金的研究表明：随着变形温度的升高和应变速率的降低合金的组织倾向于再结晶组织。SRIVATSAN等[8]对7150铝合金的准静态变形及断裂行为进行了研究，此外，KAMP等[9]和FAN等[10]分别对7150铝合金析出相及焊接性能进行了研究。然而，目前未见关于7150铝合金热变形流变应力行为和热变形组织演化规律的研究报道。为此，本文作者在 Gleeble-1500热模拟机上对 7150铝合金圆柱试样进行等温压缩的基础上，研究该合金的热变形流变应力行为及显微组织演化规律，为制定与优化 7150铝合金加工工艺以及工业生产提供了理论依据。

1 实验

1.1 实验材料

本实验所用的7150铝合金是由苏州有色金属研究院有限公司提供的厚度为115 mm的半连续铸锭，其主要合金成分(质量分数)为：5.9%~6.9%Zn，2.0%~2.7%Mg，1.9%~2.5%Cu，0.08%~0.15%Fe，0.12%Si，0.1%Mn，0.04%Cr，0.06%Ti，余量为Al。铸锭于460 ℃均匀化处理24 h，水淬后，加工成尺寸为d 10 mm×15 mm、两端带有深0.2 mm 凹槽的圆柱试样。

1.2 实验方法

将加工好的试样在Gleeble-1500热模拟机上进行等温压缩实验，压缩前圆柱试样两端的凹槽内填充75%石墨+20%机油+5%硝酸三甲苯脂作为润滑剂，以减少摩擦对应力状态的影响。变形温度范围为300~450 ℃，应变速率范围为0.01~10 s-1，压缩率为50%，升温速率为 2 ℃/s，变形前保温 3 min。由Gleeble-1500热模拟机自动采集应力、应变、压力、位移、温度及时间等数据，绘制真应力—真应变曲线。压缩后的试样迅速水冷到室温以保留热变形组织，采用 MM-6光学金相显微镜观察合金压缩变形后的金相组织。

2 结果与讨论

2.1 真应力—应变曲线

图1所示为7150铝合金在高温等温压缩变形的真应力—真应变曲线。由图1可见，在变形温度300~450 ℃和应变速率为0.01~10 s-1的条件下，流变应力随应变量的增加而迅速升高，达到峰值后逐渐下降至稳态值，进入稳态变形阶段。该现象是由于合金在塑性变形过程中，加工硬化和动态软化同时进行。在变形初期，外加应力使位错密度增加，位错间的交互作用增大了位错运动的阻力，交滑移引起的软化不足以克服位错密度增加带来的硬化，因此，在峰值应力之前加工硬化处于主导地位，应力水平迅速上升；随着应变量的增加，晶内储存能的水平逐渐升高，动态软化与加工硬化达到动态平衡，从而在稳态变形阶段的流变应力基本不变。

在同一应变速率下，7150铝合金的流变应力随着温度的升高而明显下降，这是由于变形温度升高使金属原子动能增加，位错运动的阻力下降，空位、间隙原子等点缺陷也更加活跃，从而产生动态软化降低流变应力；在同一变形温度下，7150铝合金的流变应力随着应变速率的增大而增大，这说明该合金在该实验条件下具有正的应变速率敏感性。

此外，由图1(e)可知，应变速率为10 s-1，变形温度为300~450 ℃的4条曲线均出现了一个明显波浪峰，这主要是由于在应变速率较大的条件下，温升效应使实际变形温度高于预设变形温度。

2.2 流变应力方程

在热变形过程中，材料在任何应变或稳态下的高温流变应力σ强烈地取决于变形温度T和应变速率ε˙，通常可采用SELLARS等[11]提出的双曲正弦形式加以描述：

ε˙= A F (σ )exp[-Q/(RT)] (1)

式中：)(σF为应力的函数，在不同的条件下分别可以表示为以下3种形式：

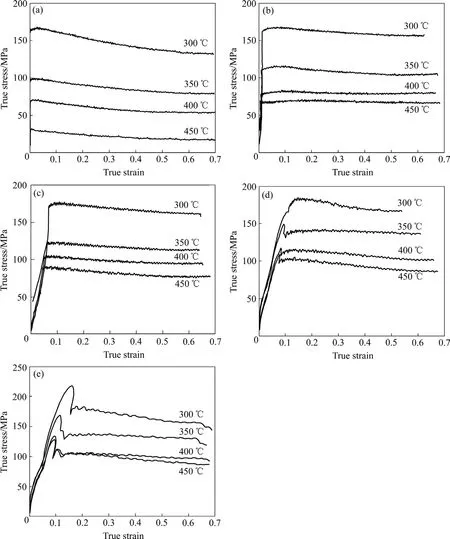
图1 不同变形温度和应变速率下7150铝合金热压缩变形真应力—真应变曲线Fig.1 True stress—true strain curves of 7150 aluminum alloy by hot compression at different deformation temperatures and strain rates: (a) ε˙=0.01 s-1; (B) ε˙=0.1 s-1;(c) ε˙=1 s-1; (d) ε˙=5 s-1; (e) ε˙=10 s-1

对所有应力状态式(1)可表示为

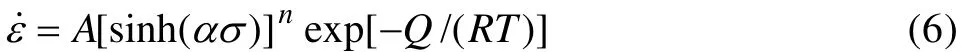
式中：α、n、A、β 为常数，α为应力水平参数(mm2·N-1)；n为应力指数；A为结构因子(s-1)；Q为热激活能，是材料在热变形过程中重要的力学性能参数，反映材料热变形的难易程度；T为绝对温度；R为气体常数；ε˙为应变速率。求出α、n、A、Q，即可描述材料的高温流变特性。大量的研究结果表明[12-14]，式(6)能较好地描述压缩、扭转、挤压等常规的热加工变形。

另外，SELLARS和TEGART提出并实验验证了热变形条件通常可用温度补偿的应变速率因子Zener-Hollomon参数Z来描述[11,15]：

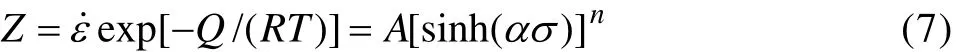
研究表明，在低应力水平下，流变应力σ和Z可用指数关系描述，而在高应力水平下可用幂指数关系描述，在整个应力水平下可用双曲函数关系描述。实际上，式(7)在形式上与式(6)是一致的。对式(2)和(3)两边取对数：

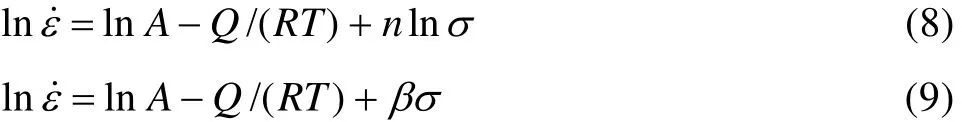
由式(6)可得：

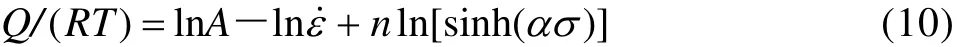
考虑到峰值应力均出现在应变较小的时刻,温升修正前后峰值变化并不明显，为方便计算，取相应ε˙、T条件下的真实峰值应力，分别以lnσ和 ln ε ˙、σ和 ln ε˙为坐标作图，如图2所示。由式(8)可知直线 ln ε ˙—lnσ的斜率，设为 n1；由式(9)可知直线 ln ε ˙—σ 的斜率，设为 β。采用最小二乘法线性回归，n1取图 2(a)中峰值应力较低的 3条直线(即变形温度为 350、400和450 ℃)斜率的平均值； β取图2(b)中峰值应力较高的3条直线(即变形温度为300、350和400 ℃)斜率的平均值；α的值可以通过式(5)求出。

计算得α=β/n=0.009 777。

在一定的应变和应变速率下，由式(10)对1/T求偏导，得

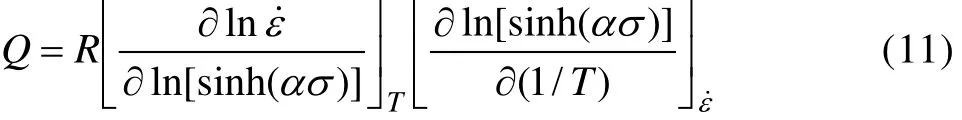
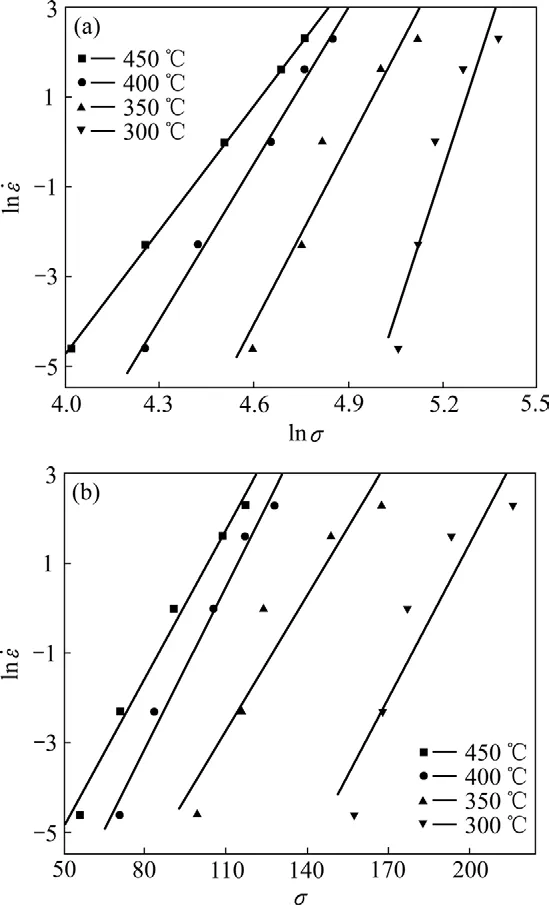
图2 不同变形温度下应变速率与流变应力之间的关系Fig.2 Relationship between strain rate and flow stress at different deformation temperatures: (a) lnσ— ε˙ln ; (b) σ— ε˙ ln

由式(11)知，当 Q 与温度无关时，ln[sinh(ασ)]与1/T的关系为线性关系，令式中 K=d{l n [sinh(ασ) ]}/d(1/T )，K 为直线 1/T—ln[sinh(ασ)]的斜率；n2为直线 ln[sinh(ασ)]— ln ε ˙的斜率。取峰值应力和对应温度值，绘制相应的ln[sinh(ασ)]— ln ε ˙图，采用最小二乘法线性回归，得n2=8.505 587；再将n2值代入式(5)得到一个调整后的 α′值，α′＝β/n2=0.013 149，将调整后的α′值重新代入式(11)，取峰值应力和对应温度值，绘制相应的 ln[sinh(ασ)]— l n ε ˙图以及103/T—ln[sinh(ασ)]图，如图3和4所示。采用最小二乘法线性回归，n3值取图3中400、350和300 ℃ 3条直线斜率的平均值，得到调整后的n3=7.228 327，K值取图 4中 5条直线斜率的平均值(3.774 074)，则Q=RnK= 226.698 8 kJ/mol。更精确的α、Q值可通过式(5)与式(11)求出，重复上面的步骤可以得到精确的各参数值。

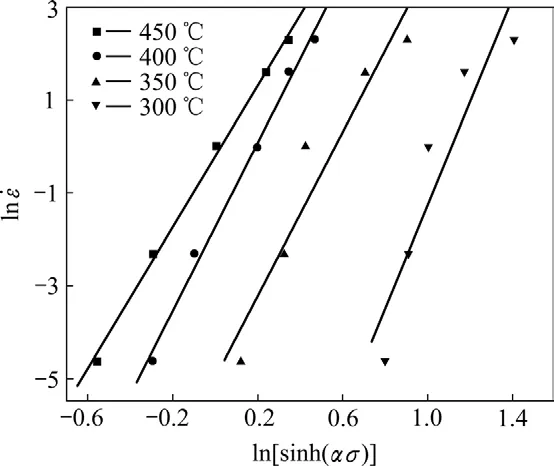
图3 不同变形温度下应变速率与流变应力的关系Fig.3 Relationship between strain rate and flow stress at different deformation temperatures

图4 不同应变速率下流变应力与变形温度的关系Fig.4 Relationship between flow stress and deformation temperature at different strain rates

对式(7)求对数得

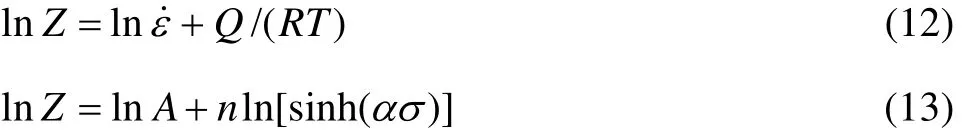
式中：lnA为直线ln[sinh(ασ)]—lnZ的截距。取一定的ε˙、Q 与 T，求得对应的 lnZ值。取 lnZ和对应的ln[sinh(ασ)]，采用最小二乘法线性回归法绘制相应的ln[sinh(ασ)]—lnZ 曲线(见图 5)，得 lnA=34.542 04。

将所求得的参数代入式(6)可得实验合金的应力—应变关系方程如下：

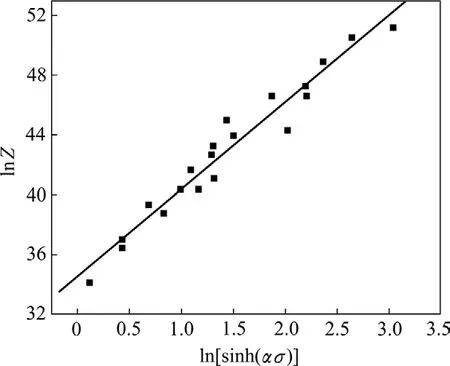
图5 lnZ与 ln[sinh(ασ)]之间的关系Fig.5 Relationship between flow stress and Zener-Hollomon parameter

ε˙=1.003 2 7×1015[ sinh(0.013 149σ)]7.228327×

2.3 高温压缩过程中显微组织的演化规律

图 6所示为不同变形条件下合金的金相显微组织。由图6可见，在变形温度为450 ℃、应变速率为0.01和0.1 s-1的条件下，合金发生了动态再结晶。在变形的晶粒界面出现较多大小不一的晶核，这些晶核即为再结晶晶核(见图6(a)和6(b))。随着再结晶晶核的不断产生和其晶界不断移动吞噬四周的变形晶粒而长大成等轴晶，最后将完全替换原有变形组织。同样，在变形温度为450 ℃、应变速率为1和10 s-1的条件下，很难观察到再结晶晶核(见图 6(c)和(d))。这是由于塑性变形的过程比较复杂，需要一定的时间来进行，应变速率高时，变形时间短，使得动态回复与动态再结晶还来不及充分发生。由图 6(c)可见，当变形温度为450 ℃、应变速率为1 s-1时，出现锯齿状晶界，该现象属于典型的几何动态再结晶。锯齿状晶界即由两个大角度晶界和一个小角度晶界形成的三叉点。在较低应变速率下，随着变形的进行，晶粒继续变细长，大角度晶界面积变大，最终原始晶粒变细到它的厚度约等于两个亚晶大小，晶粒两边的锯齿晶界互相接触，导致晶粒被夹断，由此形成的新晶粒即为再结晶晶粒。

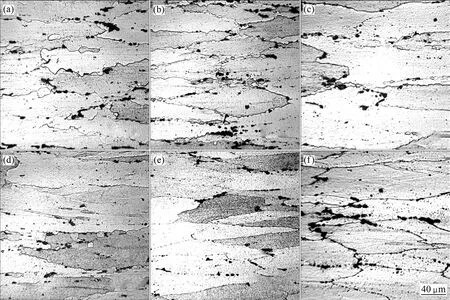
图6 不同变形条件下合金的光学显微组织Fig.6 Optical microstructures of specimens after being compressed under different conditions: (a) 450 , 0.01℃ s-1; (b) 450 ,℃0.1 s-1; (c) 450 ,℃ 1 s-1; (d) 450 ,℃ 10 s-1; (e) 400 ,℃ 0.01 s-1; (f) 300 ,℃ 0.01 s-1

当应变速率为 0.01 s-1，变形温度分别为 400和300 ℃时，热压缩后合金晶粒沿垂直压缩方向伸长，热变形组织为纤维状组织(图6(e)和(f))，表明合金仅发生了动态回复。进入稳态变形阶段的主要软化机制为动态回复，即在热激活的作用下空位浓度下降，螺位错的交滑移及刃位错的攀移，造成位错对消和重排，并形成封闭的胞壁，把晶体分割成许多低位错密度小区。随着变形的进行，位错胞壁发生多边形化形成规则的边界，形成小角亚晶。一般认为铝的层错能很高，是典型的动态回复材料，通常在较低的应变速率下发生动态再结晶[16-17]。在应变速率为0.01 s-1的条件下，变形温度为450 ℃时，合金的主要软化机制为动态再结晶；变形温度为400 ℃和300 ℃时，合金的主要软化机制为动态回复，这说明7150铝合金的再结晶激活能较高，这与在前面求得的激活能 Q＝226.698 8 kJ/mol是一致的。

3 结论

1) 7150铝合金高温压缩变形时的流变应力随变形温度的升高而减小，随应变速率的增加而增大。在应变速率为10 s-1的条件下，由于温升效应，流变应力到达峰值以后迅速下降，随后也趋于平稳。

2) 7150铝合金高温流变应力σ与形变温度T与应变 速 率 ε˙之 间 满 足 关 系 ε˙=1.00327×1015×形激活能Q＝226.698 8 (kJ/mol)

3) 在较低的应变速率下，变形温度为450 ℃时，7150铝合金的主要软化机制为动态再结晶；变形温度低于450 ℃时，合金的主要软化机制为动态回复。

REFERENCES

[1] IMMARIGEON J P, HOLT R T, KOUL A K, ZHAO L,WALLACE W, BEDDOES J C. Light weight materials for aircraft applications[J]. Materials Characterization, 1995, 35:41-67.

[2] HEINZ A, HASZLER A, KEIDEL C, MOLDENHAUER S,BENEDICTUS R, MILLER W S. Recent development in aluminium alloys for aerospace applications[J]. Mater Sci Eng A,2000, 280: 102-107.

[3] WILLIAMS JAMES C, STARKE EDGAR A Jr. Progress in structural materials for aerospace systems[J]. Acta Materialia,2003; 51: 5775-99.

[4] SRIVATSAN T S, VASUDEVAN S, PARK L. The tensile deformation and fracture behavior of friction stir welded aluminum alloy 2024[J]. Mater Sci Eng A, 2007, 466(1/2):235-245.

[5] HU H E, ZHEN L, YANG L, SHAO W Z, ZHANG B Y.Deformation behavior and microstructure evolution of 7050 aluminum alloy during high temperature deformation[J]. Mater Sci Eng A, 2008, 488(1/2): 64-71.

[6] HU H E, ZHEN L, ZHANG B Y, YANG L, CHEN J Z.Microstructure characterization of 7050 aluminum alloy during dynamic recrystallization and dynamic recovery[J]. Materials Characterization, 2008, 59(9): 1185-1189.

[7] LIN G Y, ZHANG Z F, ZHANG H, PENG D S, ZHOU J. Study on the hot deformation behaviors of Al-Zn-Mg-Cu-Cr aluminum alloy[J]. Acta Metallurgica Sinica (English Letters), 2008, 21(2):109-115.

[8] SRIVATSAN T S, GURUPRASAD G, VASUDEVAN V K. The quasi static deformation and fracture behavior of aluminum alloy 7150[J]. Materials & Design, 2008, 29(4): 742-751.

[9] KAMP N, SULLIVAN A, ROBSON J D. Modeling of friction stir welding of 7×××aluminium alloys[J]. Mater Sci Eng A, 2007,466(1/2): 246-255.

[10] FAN Xi-gang, JIANG Da-ming, MENG Qing-chang, LAI Zhong-hong, ZHANG Xin-mei. Characterization of precipitation microstructure and properties of 7150 aluminium alloy[J]. Mater Sci Eng A, 2006, 427(1/2): 130-135.

[11] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metall, 1966, 14: 1136-1138.

[12] MCQUEEN H J, YUE S, RYAN N D, FRY E. Hot working characteristics of steels in austenitic state[J]. J Mater Process Technol, 1995, 53(1/2): 293-310.

[13] MCQUEEN H J, FRY E, BELLING J. Comparative constitutive constants for hot working of Al-4.4Mg-0.7Mn (AA5083)[J].Journal of Materials Engineering and Performance, 2001, 10(2):164-172.

[14] HU Hui-e, YANG Li, ZHEN Liang, SHAO Wen-zhu, ZHANG Bao-you. Relationship between boundary misorientation angle and true strain during high temperature deformation of 7050 aluminum alloy[J]. Trans Nonferrous Met Soc China, 2008,18(4): 795-798.

[15] ZENER C, HOLLOMON J H. Effect of strain-rate upon the plastic flow of steel[J]. J Appl Phys, 1944, 15(1): 22-27.

[16] 毛卫民, 赵新兵. 金属的再结晶与晶粒长大[M]. 北京: 冶金工业出版社, 1994.MAO Wei-min, ZHAO Xin-bing. Recrystallization and grain growth of metals[M]. Beijing: Metallurgical Industry Press, l994.

[17] 李慧中, 梁霄鹏, 张新明, 黄伯云, 张传福. 2519铝合金热变形组织演化[J]. 中国有色金属学报, 2008, 18(2): 226-230.LI Hui-zhong, LIANG Xiao-peng, ZHANG Xin-ming, HUANG Bai-yun, ZHANG Chuan-fu. Microstructure evolution of 2519 aluminum ahoy during hot deformation[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(2): 226-230.

Flow stress behavior of 7150 aluminum alloy during hot compression deformation at elevated temperature

KOU Lin-yuan1, JIN Neng-ping1, ZHANG Hui1, HAN Yi2, WU Wen-xiang2, LI Luo-xing1
(1. College of Materials Science and Engineering, Hunan University, Changsha 410082, China;2. Suzhou Nonferrous Metals Research Institute, Suzhou 215026, China)

The flow stress behavior of 7150 aluminum alloy during hot compression deformation was studied by thermal simulation test at the deformation temperature of 300-450 ℃ and the strain rate of 0.01-10 s-1on the Gleeble-1500 thermal-mechanical simulator. The results show that the flow stress increases with increasing strain and tends to be constant after a peak value. The peak stress increases with increasing strain rate, and decreases with increasing deformation temperature, which can be represented by a Zener-Hollomon parameter in the hyperbolic sine equation with the hot deformation activation energy of 226.6988 kJ/mol. With increasing temperature and decreasing strain rate, the elongated grains in the deformed samples are coarsened and the size of subgrain increases; the number of fine grain in grain boundary also increases, indicating that the main softening mechanism of the alloy during hot compression deformation transforms from dynamic recovery to dynamic recrystallization.

7150 aluminum alloy; hot compression deformation; flow stress; hot deformation activation energy;recrystallization

TG 146.21

A

1004-0609(2010)01-0043-06

2008-11-10；

2009-02-27

张 辉，教授，博士；电话：0731-88664086；E-mail: zhanghui63hunu@163.com

(编辑 李向群)