水平定向钻穿越工程的项目风险评价

沈 华,马保松,吴浪辉,肖 威

0 引言

非开挖是一门新兴的铺管技术,指利用岩土导向、定向钻进等手段,在地表不挖槽的情况下,铺设、更换或修复各种地下管线的施工新技术[1]。随着我国西气东输以及城市化进程的加快,人们对地下管线建设的要求越来越来高,传统的开挖方法正遭到淘汰,而非开挖技术越来越得到广泛的应用。而水平定向钻穿越作为新兴的非开挖工程中的一种重要的技术,在一些无法实施开挖作业的地区铺设管线方面,如穿越公路、铁路、建筑物、河流、古迹保护区、闹市区、农作物及植被保护区等,取得了显著的社会经济效益[2]。然而现今大型的水平定向钻穿越工程投资动辄数千万,且施工多在地下进行,这就使得工程项目不可避免存在很多风险,若操作不当,可能造成巨大的经济损失。因此,对工程事先进行风险评价,为工程项目的实施提供一个可供指导的信息就显得十分必要[3]。目前风险评价已经在工程建设的各个领域都有应用,建设项目的风险评价也越来越受到重视[4],但是针对地下管道水平定向钻穿越工程的项目还不多,目前只有杨伟、苏欣等人做过基于模糊层次分析法的水平定向钻穿越优选方案的研究[5,6]。因此,本文结合某工程实例针对水平定向钻管道穿越工程进行了风险评价,以期对工程实际起到一定的指导作用。

1 评价方法的选择

风险评价就是要对风险进行定量分析判断,确定出风险的大小,为进一步的风险控制提供可用于指导操作的信息。目前,项目风险评价的方法很多,如层次分析法、主观评分法、决策树法、网络分析法、模糊评价法[7],而在工程项目中应用较多的是模糊综合评价法和层次分析法。模糊综合评判方法(Fuzzy Comprehensive Evaluation)是一种运用模糊变换推理分析和评价模糊系统的方法,它以模糊推理为主,定性和定量结合,精确与非精确统一进行项目的综合评判[8]。由于这种方法在处理各种难以精确描述的复杂系统问题方面表现出独特优越性,因此得到广泛的应用。层次分析法(Analytical Hierarchy Process)是美国运筹学家匹茨堡大学教授萨蒂(T.L.Satty)于 20世纪 70年代初所提出的一种层次权重决策分析方法,现今也已十分成熟,应用十分广泛[9,10]。

本文利用两种方法各自的优点,将层次分析法的权重决策与模糊综合评价法的模糊评判理论相结合,对某水平定向钻穿越工程进行了项目的风险评估。

2 项目评价的理论原理及其过程

2.1 建立风险评价指标体系

风险评价指标体系是进行项目风险评估的基础。大型工程项目的风险有人为管理的缺陷,也有材料、设备本身的缺陷,参照 Delphi法[11],该穿越工程项目部组织相关领域 20余名专家进行调查和反馈,得出该工程项目所存在的风险,本文根据此建立了一个风险评价指标体系 (如表 1所示)。该工程的风险指标体系分为 3层:

第一层是系统的总的风险度,它直接反映系统所处的总的风险等级,为项目的工程实际提供参考;

第二层是制约和影响系统总风险度的 4个主要的一级指标,它们分别是环境风险、材料与设备风险、施工风险、设计风险和承包商风险。

第三层是影响风险的 18个子因素集,也叫做二级指标,环境风险里面的场地的危险性,场地生活垃圾、泥浆、动力用油等对环境的危害,暴雨、洪水等对施工进度的影响,场地的障碍物和稳定性等;设备、材料风险里面主要包括了钻机设备、数据采集系统、防护系统如防止卡钻设备、各种应急系统以及运输状况等;施工风险里面又包括了管道回拉时表面防腐层的保护、光缆和套管的保护、施工操作及安全等这些会在施工阶段造成影响和必须注意的问题;然后就是设计风险,设计的合理性,直接关系项目的成功实施,而设计图纸交付的及时性则会影响工程实施的进度。

表1 该穿越工程风险指标体系

2.2 指标权重的计算

2.2.1 构造判断矩阵

工程项目的风险评价指标体系建立起来之后,参照层次分析法,请相关专家对指标层各元素进行两两比较评分,再写成矩阵形式。项目风险评分值采用 T.L.Satty[9]所提出的评价尺度,其表示的含义如表 2所示。当认为风险介于两个相对程度中间时,对应的分值可取中间值,例如甲与乙相比的程度介于极重要和很重要之间,则分值取 8。

表2 项目风险评分

2.2.2 一致性检验及权向量的确定

判断矩阵得出来之后,还要进行一致性检验,以避免出现 A比 B重要,B比 C重要,而 C却比 A重要的逻辑错误。

矩阵一致性的检验采用 Satty提出的一致性系数 CI和随机一致性指标 R I以及随机一致性比率CR的方法来进行。

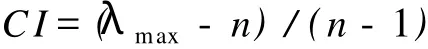
式中:λmax——所得矩阵的最大特征值;n——矩阵的维数。

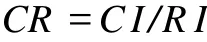
R I是随机一致性指标,一般认为 CR≤0.1时,所得出的矩阵具有较好的一致性。其对应数值如表3。

表3 随机一致性指标 RI的数值

当判断矩阵的不一致程度在容许的范围内时,可用其特征向量作为权向量,否则就要重新进行成对比较,对矩阵进行调整。本文利用Matlab平台强大的矩阵运算功能,以及可以与 Excel互动的优点,把一致性检验、权向量计算统一用一个程序来实现[12]。

2.3 模糊集的建立

指标权重计算出来后,我们再根据模糊综合评判理论建立评语集,以及各因素的隶属度向量,进行最后的评价。

该工程项目风险一级指标为 B,B={B1,B2,B3,B4,B5},相应的权重为W,其各自所属的二级指标 Ci(i=1,2,…,n)的权重为 W1,W2,W3,W4,W5。

同时设模糊评语集为 V={无风险,低风险,中等风险,高风险,极高风险},以向量 C={10,30,50,70,90}T表示其对应的分值。

2.4 模糊综合评判及相对隶属度向量的确定

对项目风险指标进行模糊综合评判,通过组织专家讨论各个因素对评语集的隶属度,得到各风险隶属度向量。例如通过专家讨论得出环境风险中现场操作环境的危险性 (C1)对于评价结果是:有 13%的人认为无风险,35%的人认为低风险,39%的人认为中等风险,8.7%的人认为高风险,4.3%的人认为极高风险,则得出的评判结果为 (0.13,0.35,0.39,0.087,0.043)。同样对其它 3个因素进行评价得到环境风险所对应的隶属度向量 R1,再对 B层其它 4个因素进行评价依次得到隶属度向量 R2,R3,R4,R5。对 Ri(i=1,2,…,5)进行归一化处理,再运用矩阵的模糊乘法,得到 B层所有因素对评语集的总的隶属度向量:B=WioRi(i=1,2,3,4,5),其中 o为取大取小算子[8]。

2.5 评估结果

由 S=B·C就可以得到工程项目的风险总值,从而确定该项目的风险水平。

3 穿越工程风险计算

3.1 判断矩阵的建立及其一致性检验

环境风险 (B1)判断矩阵,材料、设备风险 (B2)判断矩阵,施工风险 (B3)判断矩阵,设计风险 (B4)判断矩阵,承包商风险 (B5)判断矩阵,B层所有因素相对于 A层的判断矩阵分别见表 4～9。

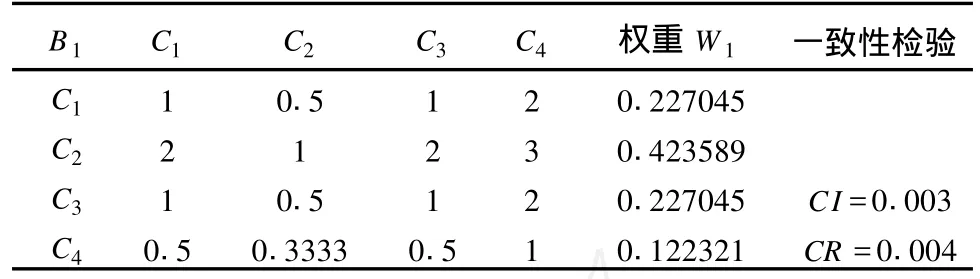
表4 环境风险(B1)判断矩阵

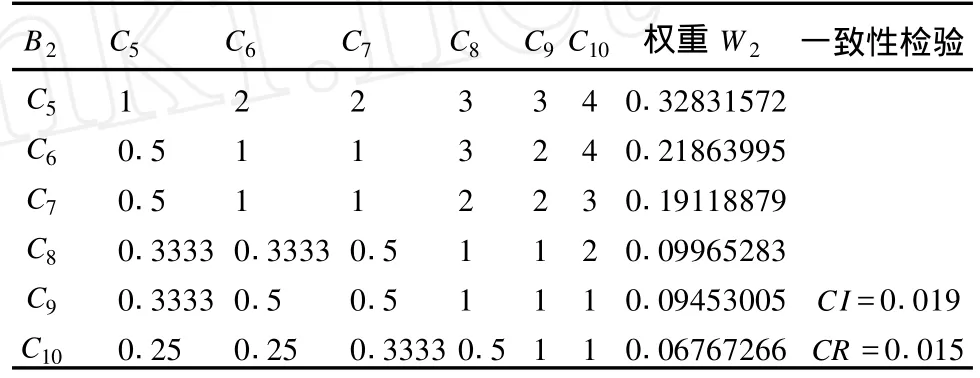
表5 材料、设备风险 (B2)判断矩阵

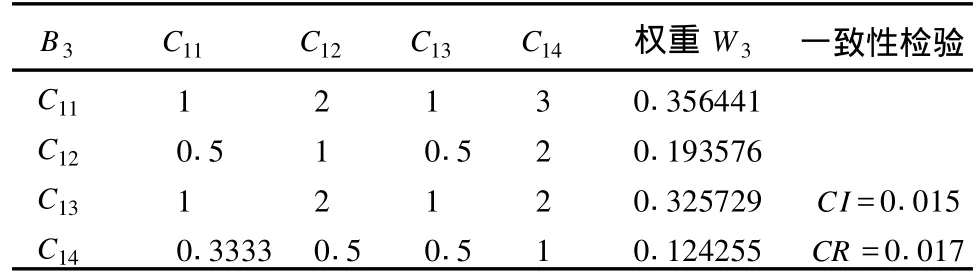
表6 施工风险(B3)判断矩阵

表7 设计风险(B4)判断矩阵

表8 承包商风险 (B5)判断矩阵

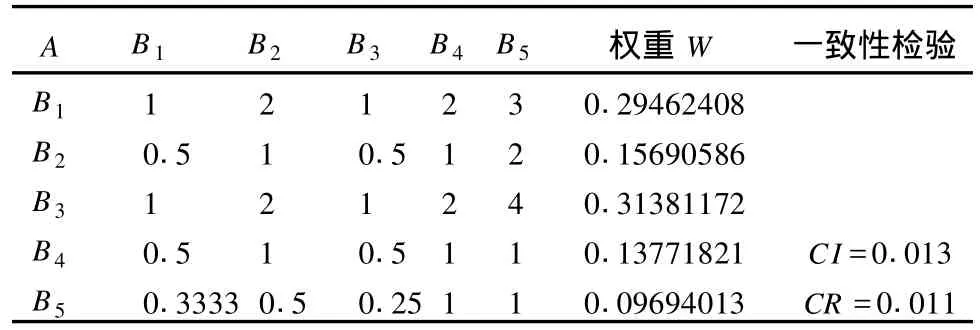
表9 B层所有因素相对于A层的判断矩阵

3.2 权重的计算

通过矩阵的特征值和特征向量以及一致性检验的Matlab计算程序,对表 1所建立的风险指标体系得出的判断矩阵得到各层次因素的权重分别为:

3.3 各个风险因素的隶属度归一化矩阵

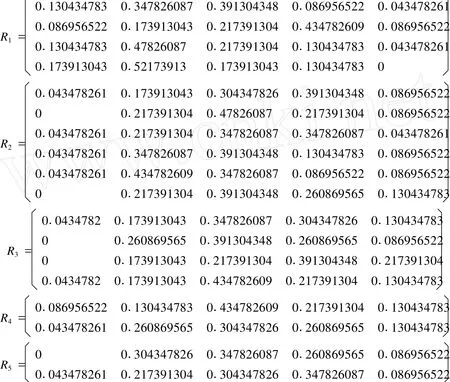
3.4 合成隶属度向量

在Matlab平台上,通过调用相应的模糊乘法的取大取小函数,运用矩阵的模糊乘法将各个权重向量和对应的隶属度矩阵相乘得到合成隶属度矩阵 R并归一化:

而得到矩阵 R=(B1,B2,B3,B4,B5)T。

再次运用矩阵的模糊乘法将总权重向量W与合成隶属度矩阵 R相乘得到综合评判结果 B并归一化,得到:

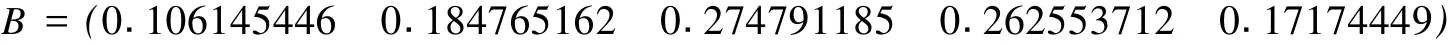
3.5 计算最终的风险值

将最终的评判结果与评语集相乘得到最终的风险值:S=B·C=54.18。将最后的风险值与相应的评语集 V和评价分向量 C相比较,可知该风险值处于中等风险范围,风险级别较高,应当引起承包商以及项目部的重视。而由权重向量W可知环境风险和施工风险是影响比较大的因素,施工单位及项目部应加强施工和环境保护这 2个方面的工作。

4 结论

层次分析法是一种半定性与半定量的方法,具有系统、实用、简洁的特点,可以用来确定 HDD穿越工程中各风险因素相对总风险系统的权重。而模糊综合评价法是一种以模糊推理为主的半定性与半定量方法,可以用来求出系统总的风险度,根据最大隶属度原理判断穿越工程项目风险的等级。所以层次分析法和模糊综合评价法结合在一起,可以达到互补,比原来的单一方法有所改进,是一种有效的风险评估方法。

[1] 马保松.非开挖工程学[M].北京:人民交通出版社,2008.3-15.

[2] 颜纯文,蒋国盛,叶建良.非开挖铺设地下管线工程技术 [M].上海:上海科学技术出版社,2005.3-22.

[3] 郑海中.地质工程项目风险管理研究及应用[D].长沙:中南大学,2008.1-7.

[4] 许家雄.建设工程项目的风险管理的研究与应用[D].南昌:南昌大学,2006.1-10.

[5] 杨伟,李佩.管道穿越方案的模糊层次优选 [J].油气储运,2007,26(1):44-46.

[6] 苏欣,黄坤,杨华,等.模糊层次分析法在优选管道穿越方案中的应用[J].石油天然气学报,2005,27(6):801-802.

[7] 郝海,踪家峰.系统分析与评价方法[M].北京:经济科学出版社,2007.23-35.

[8] 谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中理工大学出版社,2000.1-49.

[9] T.L.Saaty.The Analytic Hierarchy Process[M].New York:McGraw-Hill,1980.

[10] Saaty T.L.A Scaling Method for priorities in Hierachy Structures[J].Journal of Math,Psychology,1997,(15):234-281.

[11] 王英凯.基于德尔菲法和层次分析法原理的科研项目评价模型[J].山西财经大学学报,2001,23(S1):148-149.

[12] 李工农,阮晓青,徐晨.经济预测与决策及其 Matlab实现[M].北京:清华大学出版社,2007.144-195.