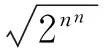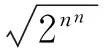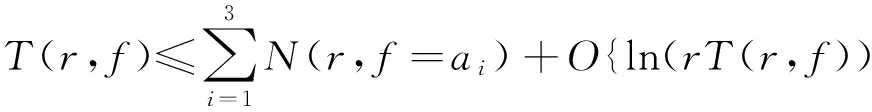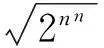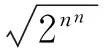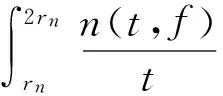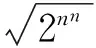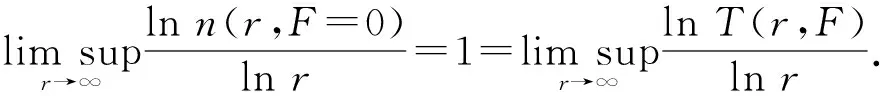关于亚纯函数例外值的例

彭炎红, 孙道椿

(华南师范大学数学科学学院,广东广州 510631)

关于亚纯函数例外值的例

彭炎红, 孙道椿*

(华南师范大学数学科学学院,广东广州 510631)

在亚纯函数的Valiron例外值、Borel例外值以及T例外值概念的基础上,考察它们之间的相互关系，重要的是构造了一亚纯函数,以0为Valiron例外值,但0不是其Borel例外值,也不是T例外值.

亚纯函数; Borel例外值; Valiron例外值; T例外值

1 引言与结果

在亚纯函数理论中, Borel定理的证明产生了值分布理论的萌芽，1925年, Nevanlinna为值分布论的发展做出了划时代的贡献,创立了Nevanlinna理论,构建了值分布论的基本理论.70多年来,值分布理论在Nevanlinna理论的影响下取得了巨大的发展.我国的值分布论研究始于熊庆来先生, 他与庄圻泰等函数论专家为我国培养了一支宝贵的值分布论研究队伍.近20年来我国关于亚纯函数值分布论的研究又取得了新的发展,形成了以杨乐为首的, 在国际上被誉为“中国学派”的值分布论研究群体.从值分布的一般理论可以看出,亚纯函数f(z)的模分布性质说明了f(z)在整个开平面上的某种取值情况,而f(z)的辐角分布性质则反映了f(z)在某条射线附近的取值情况. 杨乐和张广厚[1]曾创造性地研究了辐角分布与模分布的关系,他们首次在这2个看似无关的问题间发生了明确的关系.而亚纯函数的奇异方向是值分布论中研究最多的问题之一[2],是辐角分布论的典范,其例外值及相互关系也是值分布论中的基本内容, 且与奇异方向紧密相关.大多数人都是在研究奇异方向时介绍到相应的例外值,而避开奇异方向单独讨论亚纯函数例外值的文献较少见, 且一般是介绍或引进一些重要例外值相关的定理和结论, 以构造例子的形式来探讨例外值的文章就更加罕见, 而且构造关于例外值的例子, 对以后亚纯函数奇异方向的研究也有极大的参考价值. 本文依据亚纯函数的Borel例外值一定是其Valiron例外值, 但Valiron例外值未必是Borel例外值的事实, 初步尝试构造了一个以0为Valiron例外值, 但不是 Borel例外值,也不是T例外值的亚纯函数. 其构造思想源于文献[3].

下面叙述几个相关的定义:

定义1[4]设f(z)于开平面上亚纯,f(z)的级定义为：

定义2[4]设f(z)为开平面上亚纯的函数, 级为有穷正数,a为任一复数,a称为f(z)的Borel例外值,若

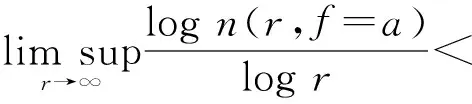
定义3 设f(z)为复平面上的亚纯函数,a为任一复数,a称为f(z)的T例外值,若

定义4[5]设f(z)为开平面上的超越亚纯函数,a为任一复数,称a为f(z)的Valiron例外值,若

在引出例子之前让我们先介绍一个命题：

命题1 设f(z)为开平面上的亚纯函数, 若a为f(z)的Borel例外值,则必为f(z)的Valiron例外值.

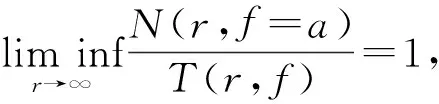
而由定义显然可知,若a为f(z)的T例外值,则它必为f(z)的Valiron例外值.那么亚纯函数的Borel例外值和T例外值都是其Valiron例外值,而Borel例外值和T例外值并不存在必然的包含关系.

以下出现的[x]均是对x进行取整.

本文的结论是：

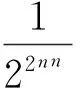
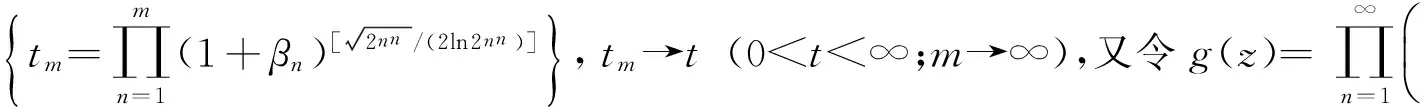
2 几个引理

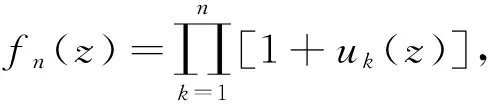
以下出现的F(z),f(z),g(z)都是指上面结论中所构造的F(z),f(z),g(z).

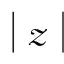
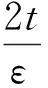
证明1)先证前半部分,令

显然b1,b2,…,bn,…是f1(z)的无限个零点,它们的模满足:

|b1|<|b2|<…<|bn|<…,

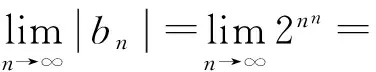
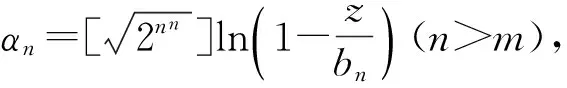
因为bn=2nn, 因此

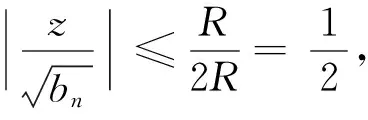
现证后半部分(证明方法参考了文献[7]),因为当|z-an|≥1,有

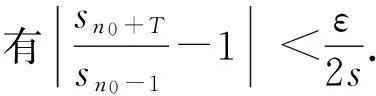
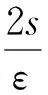
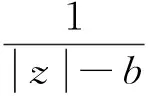
因而当|z|>M且|z-an|≥1 (n=1,2,…)时, 有

同理可证得引理中的2)成立.

引理3[8]设f在G内是亚纯的,具有极点p1,p2,…,pm和零点z1,z2,…,zm, 它们都是按重数计算的.如果γ是G内同调于零的可求长闭曲线,且不经过p1,p2,…,pm和z1,z2,…,zm,则

引理4 令Lp:|z-ap|≤p+1 (p=1,2,…),则当p>N0(N0≥N), 在每个Lp的内部,f(z)-d(d≠0)的零点数与f(z)的极点数相同.其中N由引理2中的1)所取定.

同样令Lq:|z-Aq|≤q+1 (q=1,2,…),任意选择一个复数a=d+1 (d≠0), 类似于引理4的讨论, 可推出当q>N时,在每个Lq的内部,g(z)-a的零点数与g(z)的极点数相同.

3 定理的证明

定理1的证明由引理2可知f(z)和g(z)均为亚纯的, 因此F(z)=f(z)g(z)在平面上亚纯.

(1)下面讨论F(z)的级.

对任意充分大的r, 存在相应的n,使得

bn=2nn

i)首先讨论T(r,f)如下:

(1)

n(r,f=5)=n(r-(aN+1-(N+1)),f=5)+

n((aN+1-(N+1)),f=5)=

n(r-(aN+1-(N+1)),f=5)+c=

(2)

其中c是跟N有关的一有限数. 因此类似于式(1)可得

(3)

从而由式(1)和式(3)可知

O{ln(rT(r,f))}.

(4)

ii)讨论T(r,g)如下：

n(r,g)=

i.e.n(r,g)≤

因此

(5)

类似于N(r,g)的讨论同样可得出

N(r,g=0)≤

(6)

对于g(z),设aj(j=1,2,3)分别为0,∞,5,而类似于式(2)和式(4)可得

N(r,g=5)≤

(7)

由于

则由式(5)、(6)和式(7)可得出T(r,g)满足:

(8)

O{ln(rT(r,g))}.

(9)

因此由式(4)和式(9),有

所以F(z)的级为

(2)下面证明0是F(z)的Valiron例外值, 但不是F(z)的Borel例外值和T例外值.

i)0是F(z)的Valiron例外值.

取点列{rn=2nn+2n},则

T(2rn,F)≥N(2rn,F)≥N(2rn,f)+N(2rn,g)≥

而

故

因此

从而得出0是F(z)的Valiron例外值.

ii)0不是F(z)的Borel例外值.

对于2nn

n(r,F=0)=n(r,g=0)≤

(10)

以及

n(r,F=0)=n(r,g=0)≥

(11)

iii)0不是F(z)的T例外值.

而由式(4)和式(9)可知

从而

则可得出 0不是F(z)的T例外值.

[1] YANG L, ZHANG G. Recherches sur le nombre des valeurs et le nombre des directions de Borel des fonctions méomorphes[J]. Sci Sinica, 1975, 18: 23-37.

[2] 庄圻泰. 亚纯函数的奇异方向[M]. 北京: 科学出版社,1982.

[3] 杨乐,张广厚.具有给定奇异方向亚纯函数的构造[J].中国科学,1976,5(3):308-319.

[4] 杨乐. 值分布论及其新研究[M]. 北京: 科学出版社,1982.

[5] HAYMAN W K. Meromorphic functions[M].Oxford:Clarendon Press,1964.

[6] 柏盛桄. 整函数与亚纯函数[M]. 武汉:华中师范大学出版社,1982.

[7] 孙道椿. 关于奇异方向的例[J].数学杂志,1994,14:176-182.

SUN Daochun. Examples on singular direction[J]. Journal of Mathematics, 1994, 14:176-182.

[8] CONWAY J B. Functions of one complex variable[M]. Beijing: World Publishing Corporation, 1978: 150.

Keywords： meromorphic function; Borel exceptional value; Valiron exceptional value; T exceptional value

【责任编辑 庄晓琼】

EXAMPLESONEXCEPTIONALVALUESOFMEROMORPHICFUNCTIONS

PENG Yanhong1, SUN Daochun2

(School of Mathematics, South China Normal University, Guangzhou 510631, China)

Basing on the concepts of Valiron exceptional value, Borel exceptional value and T exceptional value of meromorphic functions, the relations among them are investigated. The most important result is that a function meromorphic in the plane is constructed, with 0 as a Valiron exceptional value, but not as a Borel exceptional value, and also not as a T exceptional value.

2009-04-13

彭炎红(1984—),女,江西上饶人,华南师范大学2007级硕士研究生,主要研究方向: 函数论, Email:pengyh128888@163.com;孙道椿(1943—),男,江西南昌人,博士,华南师范大学教授,博士生导师,主要研究方向：复分析,Email: sundch@scnu.edu.cn.

*通讯作者

1000-5463(2010)02-0018-06

O174.51

A