辛三代数的Frattini子代数

倪军娜, 于建华

(华南师范大学数学科学学院，广东广州 510631)

辛三代数的Frattini子代数

倪军娜, 于建华

(华南师范大学数学科学学院，广东广州 510631)

讨论了辛三代数的Frattini子代数和Frattini 理想的性质，得到了Frattini 理想是辛三代数的幂零理想和可解balanced辛三代数的Frattini子代数等于Frattini 理想的结论.

辛三代数; Frattini子代数; Frattini理想

辛三代数是在文献[1]中首次提出来的，它是Freudenthal三系的一种更广泛的形式[2]，其上有李三系结构的一种三系. 辛三代数作为一种更广泛的代数结构受到人们更多的关注[3-6]. 群的Frattini子群理论在群论中有着重要的地位, 相似的问题在与之结合密切的Lie代数中也被提出来[7-8].尽管辛三代数不象李代数那样有很深的群背景，但是纯代数地研究Frattini子代数本身就是有意义的.本文将这种概念推广到辛三代数上.

(1)L(x,y)-L(y,x)=R(x,y)-R(y,x) (记S(x,y)=L(x,y)-L(y,x));

(2)S(x,y)R(z,w)=R(S(x,y)z,w)=R(z,S(x,y)w)=R(z,w)S(x,y);

(3)[R(x,y),R(z,w)]=R(R(z,w)x,y)+R(x,R(w,z)y),

其中R(y,z)x=L(x,y)z=M(x,z)y=xyz.

辛三代数U称为balanced如果S(x,y)=x,yId, 其中x,y是U上的反对称双线性型.

子空间B是辛三代数U的理想，如果UBU⊆B,BUU⊆B,UUB⊆B.

1 Frattini子代数

定义1 辛三代数U的一个子代数B称为极大的，如果真包含B的子代数只能是U自己.

定义2 辛三代数U的所有极大子代数的交称为U的Frattini子代数，记为F(U). 而含在F(U)中的U的极大理想称为U的Frattini理想, 记为φ(U).

命题1 设U是辛三代数，下列结论成立:

(1)如果B是U子代数使得B+F(U)=U,则B=U;

(2)如果B是U子代数使得B+φ(U)=U,则B=U.

证明如果B≠U,则必存U的一个极大子代数B1包含着B，则有B1+F(U)=U. 由定义2, 得F(U)⊆B1. 故得B1+F(U)=B1=U,这与B1是U的极大子代数矛盾. 因而B=U. 同样地，我们可以得到(2).

命题2 设B是辛三代数U的一个理想，则存在U的一个极大子代数C使得B+C=U的充分必要条件是BF(U).

证明(⟸)如果BF(U),则必存在U的一个极大子代数C使得BC.因为B是理想, 故得到B+C是U的子代数并且包含C.则由C的极大性得U=B+C.

(⟹)假设B⊆F(U)，由U=B+C⊆F(U)+C=U,得到U=F(U)+C. 由命题1, 得到C=U, 这与C的极大性矛盾.故BF(U).

命题3 设C,B分别是辛三代数U的子代数和理想，且使得B⊆F(C)(或φ(C), 则B⊆F(U)(或φ(U)).

证明如果C=U, 结论显然成立.

现假设C≠U并且BF(U). 由命题2, 必有U的极大子代数V使得U=B+V=C+V.则C=B+C∩V. 故C=B+C∩V⊆C⊆F(C)+C∩V⊆C. 即C=F(C)+C∩V. 由命题1,得到C=C∩V.故U=B+V⊆C+V⊆V. 这与V的极大性矛盾. 因此B⊆F(U). 对φ(U)可类似得到.

推论1 设B是辛三代数U的一个子代数使得F(B)(或φ(B))是U的理想，则F(B)⊆F(U)(或φ(U)).

命题4 设B是辛三代数U的理想，则下列结论成立:

(1)(F(U)+B)/B⊆F(U/B)(φ(U)+B)/B⊆φ(U/B);

(2)若B⊆F(U),则F(U)/B=F(U/B),φ(U)/B=φ(U/B);

(3)若F(U/B)=0(或φ(U/B)=0),则F(U)⊆B(或φ(U)⊆B).

证明(1) 令π:U→U/B是自然同态，显然π-1(F(U/B))=H是U的子代数且F(U/B)=H/B. 则H是U的包含B的极大子代数的交，并且有H包含F(U)和(F(U)+B)/B⊆F(U/B)=H/B. (φ(U)+B)/B⊆φ(U/B)可类似得到. 由(1), 不难得到(2)、(3).

命题5 设U是一个辛三代数，则有F(U)⊆U1. 特别地, 如果U是可换的，则F(A)=0.

证明如果U=U1, 则结论显然. 如果U≠U1且F(U)U1,那么存在一个元素xF(U),xU1和U的余维数为1的子代数B使得U1⊆B,xB. 因此B是U的不含元素x的极大子代数, 这与xF(U)矛盾. 故F(U)⊆U1.

引理1 设I是辛三代数U的理想，B是U的极小子代数使得U=I+B, 则I∩B⊆φ(B).

证明假设I∩Bφ(B),则I∩BF(B)，那么必存在B的极大子代数M使得I∩BM,且B=I∩B+M. 因此U=I+(I∩B+M)=I+M. 这与B的极小性矛盾, 故I∩B⊆φ(B).

命题6 设I是辛三代数U的可换理想且I∩φ(U)=0, 则必存在U的子代数B使得U=I⨁B.

证明选取B是满足U=I+B的最小子代数, 则由引理1有I∩B⊆φ(B). 又因为I∩B是U的理想,由推论1得到I∩B⊆I∩φ(U)=0.

定理1 如果辛三代数U有如下的直和分解：U=U1⨁…⨁Uk,其中Ui(i=1,…,k)是U的理想, 则有下列结论:

(1)F(U)⊆F(U1)⨁…⨁F(Uk);

(2)φ(U)=φ(U1)⨁…⨁φ(Uk).

证明(1)设Bi是Ui(1≤i≤k)的极大子代数，则Bi+(U1⨁…⨁i⨁…⨁Uk) 是U的极大子代数, 这里i表示Ui从和式中去掉，再令其相交就得到(1)的结果.

(x1+…+xk)UiUi=xUiUi=xiUiUi⊆

Ui∩φ(U)=φ(Ui),

Ui(x1+…+xk)Ui=UixUi=UixiUi⊆

Ui∩φ(U)=φ(Ui),

UiUi(x1+…+xk)=UiUix=UiUixi⊆

Ui∩φ(U)=φ(Ui),

故φ(Ui)+xi是U的包含于F(Ui)的理想，即xiφ(Ui)(i=1,…,k)且xφ(U1)⨁…⨁φ(Uk).

引理2 设σ是有限维向量空间V的一个线性变换，f是一个多项式使得f(σ)=0.则:

(1)如果f=f1f2且f1,f2是互素多项式,则存在σ的不变子空间V1,V2，使得V=V1⨁V2，且

f1(σ)(V1)=f2(σ)(V2)=0;

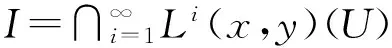
定理2 设B是辛三代数U的理想且B⊆F(U), 则B是幂零的. 特别地,φ(U)是U的幂零理想.

证明只需要证前一论断.

我们知道在U中存在理想序列

B0=B▷B1▷B2▷…▷Bt=U,

其中Bi=B▷Bi+1表示Bi是Bi+1的理想.令(x,y)=L(x,y)+R(x,y)+M(x,y)，其中x,yB.则存在整数n使得n(x,y)(U)⊆B. 由注1,U=I+H, 其中{zU|i(x,y)(z)=0,∀x,yB}.故I⊆B,U=B+H且B⊆F(U),U=F(U)+C. 由命题1,得C=U, 即是说对某个整数m和任意的zU，有m(x,y)(z)=0, 即B是幂零的.

2 可解辛三代数的Frattini子代数

命题7 设H是可解辛三代数U的极小理想，则H可换.

证明由U是可解的,得H也是可解的，故HHH≠H. 而HHH是真包含于H的理想，故必有HHH=0.

定理3 设U是可解的balanced辛三代数，则F(U)是U的理想, i.e.,F(U)=φ(U).

证明对dimU进行数学归纳. 当dimU=1时显然成立. 假设结论对k

(H∩N)UU=(H∩N)(N+H)(N+H)⊆H∩N,
U(H∩N)U=(N+H)(H∩N)(N+H)⊆H∩N,
UU(H∩N)=(N+H)(N+H)(H∩N)⊆H∩N,

得H∩N是H的理想，故H∩N=0，则U=H⨁N.

下面分2种情况讨论.

(1)若H真包含于CU(H),则N∩CU(H)是U的非零理想, 且对U的每个极大子代数N必包含U的极小理想T. 此时,F(U)=∩{F(U:T)|T是U的极小理想}是U的理想.

mxy+myx=axy+ayx+[R(x,y)+

R(y,x)](axy+ayx)=axy+ayx=0.

定义3 辛三代数U的理想I称为是Jacobson根基(记为J(U))，若I是U的所有极大理想的交.

命题8 设U是辛三代数, 则J(U)⊆U1.

证明类似于命题5.

定理4 设U是可解辛三代数，则J(U)=U1.

证明由命题8,J(U)⊆U1=U(1).故只需证明U1⊆J(U). 设I是U的一个极大理想, 则U/I是可解并无任何真理想. 故U/I必定是可换的且I⊇U(1). 这样U1⊆J(U)成立.

推论2 设U是可解辛三代数, 则F(U)⊆J(U).

定理5 设U是一个幂零辛三代数,则

(1)U的每个极大子代数都是理想;

(2)F(U)=U(1)=φ(U)=J(U).

证明(1)由U是幂零的，故存在正整数m，使得

U=U(0)⊃U1⊃…⊃Um=0.

设M是U的一个极大子代数, 则必存在整数k使得Uk+M≠M, 但Uk+1+M=M. 则有(Uk+M)*M⊆Uk+1+M=M, i.e.,M≠Uk+M⊆NU(M). 因此NU(M)=U，进而得M是U的理想.

(2)设T是U的极大子代数，则由(1),T是U的理想且U/T没有真理想.因此U/T是可换的,则U(1)⊆T且U(1)⊆F(U). 再由命题5, 得F(U)=U(1). 由(1)有F(U)=φ(U)=J(U).

推论3 设U是辛三代数,若U(1)幂零的且φ(U)=0，则U(1)可换.

证明由U(1)幂零得U是可解的. 由定理4,得F(U)=φ(U).再由定理5,得F(U(1))=φ(U(1))=(U(1))(1)=(U(1))1.故由命题3，得φ(U(1))⊆F(U). 因此

(U(1))1=φ(U(1))⊆F(U)=φ(U)=0.

即U(1)是可换的.

[1] FAULKENER J R. A construction of Lie algebras from a class of ternary algebra [J]. Trans Amer Math Soc, 1971, 155:397-408.

[2] MEYBERG K. Eine theorie der Fredenthalschen triple system [J]. Math,1968, 30:162-190.

[3] FAULKENER J R. On the structure of symplectic ternary algebras [J]. Nedrl Akad Wetebsch Proc, 1972,75: 247-256.

[4] 倪军娜，张知学. 辛三代数的幂零根[J]. 南开大学学报：自然科学版，2002,35(1):48-52.

NI Junna, ZHANG Zhixue. The nil radical for symplectic ternary algebras [J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2002, 35(1): 48-52.

[5] 董磊，朱莹，张雅静，等.辛三代数的结构群和结构代数[J].河北大学学报：自然科学版，2005,25(3):234-237.

DONG Lei, ZHU Ying, ZHANG Yajing, et al. Structure group and structure algebra of the symplectic ternary algebras [J]. Journal of Hebei University:Natural Science Edition, 2005, 25(3):234-237.

[6] 白喜梅，刘文丽. 辛三代数分解的唯一性[J]. 河北大学学报：自然科学版，2008,28(3):225-227.

BAI Ximei, LIU Wenli. The uniqueness of decomposition of sympletic ternary algebras [J]. Journal of Hebei University:Natural Science Edition, 2008,28(3):225-227.

[7] BECHTELL H. The Frattini argument for Lie algebra [J]. Math Zeit, 1973,133: 277-283.

[8] SCHEIDERER C. Intersections of maximal subalgebras in Lie algebras [J]. Journal of Algebra, 1987,105:268-270.

Keywords： symplectic ternary algebra; Frattini subalgebra; Frattini ideal

【责任编辑 庄晓琼】

THEFRATTINISUBALGEBRASOFSYMPLECTICTERNARYALGEBRAS

NI Junna, YU Jianhua

(School of Mathematics, South China Normal University, Guangzhou 510631, China)

The Frattini subalgebras and Frattini ideals of symplectic ternary algebras are studied. It is gotten that Frattini ideal of a symplectic ternary algebra is a nilpotent ideal, and the Frattini subalgebra is equal to the Frattini ideal for a solvable balanced symplectic ternary algebra.

2009-06-29

倪军娜(1973—),女,山东乳山人,博士,华南师范大学讲师,Email:nijunna@126.com.

1000-5463(2010)02-0001-03

O151.26

A