一个新的有最佳常数因子的 Hilbert型积分不等式
2010-11-18谢子填
曾 峥, 谢子填
(1.韶关学院数学与信息科学院,广东韶关 512005; 2.广东肇庆学院数学系,广东肇庆 526061)
一个新的有最佳常数因子的 Hilbert型积分不等式
曾 峥1, 谢子填2
(1.韶关学院数学与信息科学院,广东韶关 512005; 2.广东肇庆学院数学系,广东肇庆 526061)
应用权函数,给出一个新的有最佳常数因子的Hilbert型积分不等式. 同时给出它的等价式及其逆向不等式.
Hilbert积分不等式; 权函数; Hölder不等式
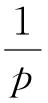
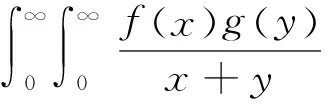
(1)
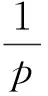
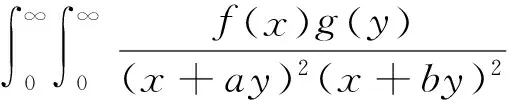
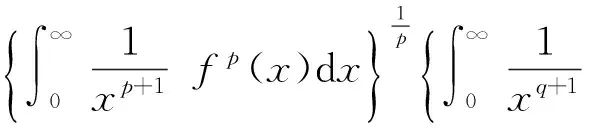
(2)
同时还考虑了a=b的情形.
2007年,杨必成在文献[4]中给出了以下2个推广的最佳常数因子的Hilbert型积分不等式:
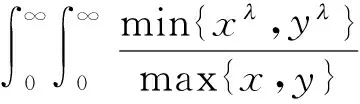
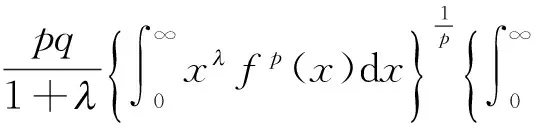
(3)
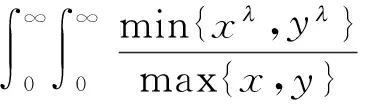
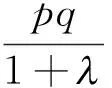

(4)
我们将应用权函数方法给出一个新的含有最佳常数因子的Hilbert型不等式的推广式,它包含了式(3)和式(4).
以下设a,b,为非负数,且2a+b=+1;p>1, 1/p+1/q=1,r>1, 1/r+1/s=1.
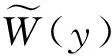
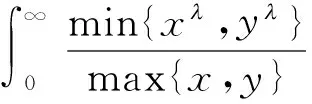
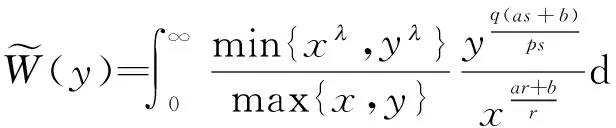
则
其中
且有
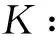
(5)
证明设y=xσ,注意2a+b=+1, 则又由x=y/σ,则
容易证明K1=K2,且
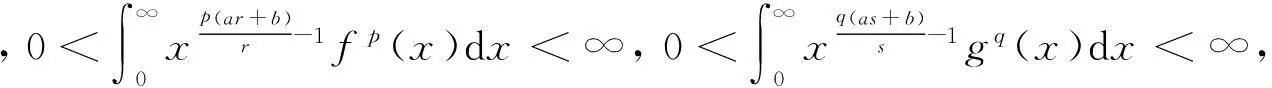
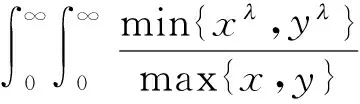
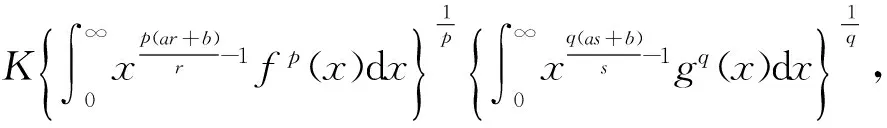
(6)
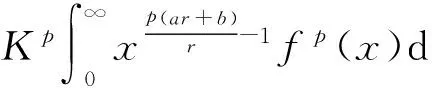
(7)
式(6)和式(7)等价,这儿常数因子K由引理1定义,且K及Kp为最佳值.
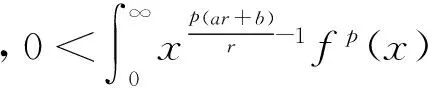
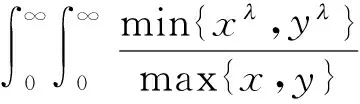
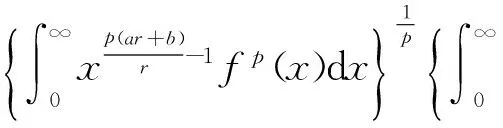
(8)
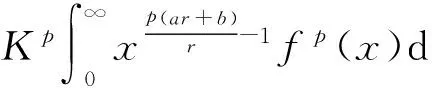
(9)
式(8)和式(9)等价,这儿常数因子K及Kp为最佳值.
我们仅证明定理1,定理2证明与之类似.
定理1的证明由带权Hölder不等式[11],有
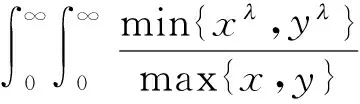
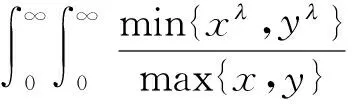
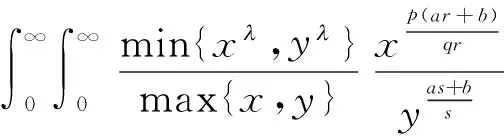
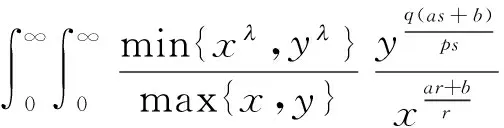
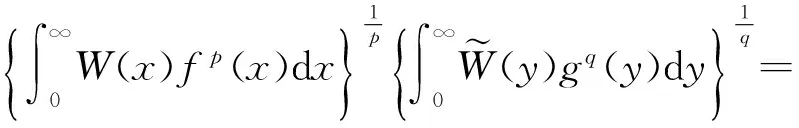
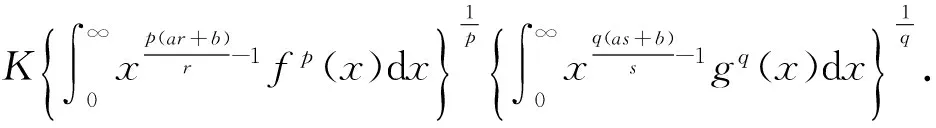
(10)
如式(10)中的不等式取等号, 则有常数M和N使得
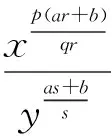
故有常数C,使
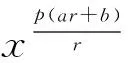
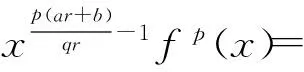

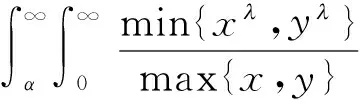
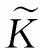
(11)
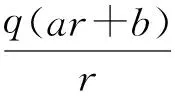
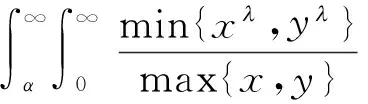
如果说以涉诉信访统计通报考评机制为代表的司法行政权力对法官的管理、制约尚具有较为隐性的特征,那么人民法院的内部监察制度则更为显性地发挥着对法官的管理、制约作用。讨论民事诉讼中的法律监督离不开人民法院监察制度,毕竟,依据《中华人民共和国法公务员法》《中华人民共和国法官法》《人民法院监察工作条例》等规范性法律文件,对法律监督范围内的民事诉讼中审判人员的违法行为,人民法院监察部门能够而且应当启动相应的监察程序、形成相应的监察结果。
(12)
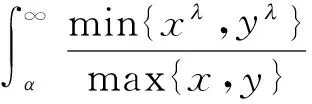
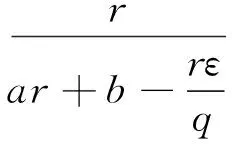
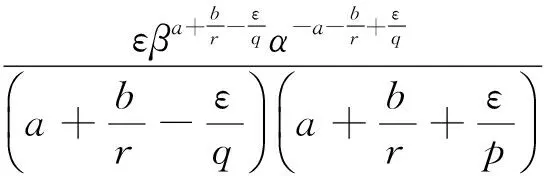
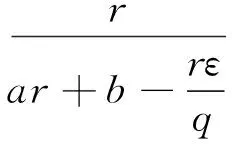
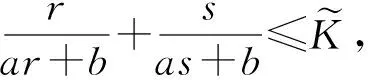
下证式(6)和式(7)等价. 记

+∞,
(13)
于是有
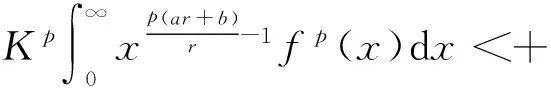
(14)

如式(7)成立,则
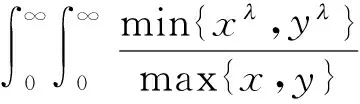
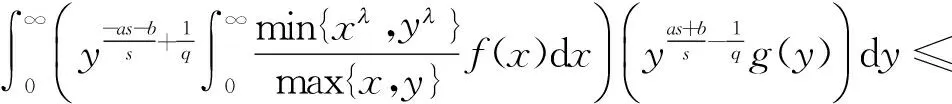
(15)
由式(15)和式(7)得式(6).
评注容易看出式(6)包含了式(3)和式(4).事实上,在式(6)中设a=0, 这时b=+1,K==,于是令s=q可得式(3);令s=p可得式(4).
致谢作者衷心感谢杨必成教授的指导和帮助!
[1] HARDY G H. Note on a theorem of Hilbert concerning series of positive terems[J].Proc Math,1925,23(2): XLV-XLVI.
[2] XIE Zitian,YANG Bicheng.A new Hilbert-type integral inequality with some parameters and its reverse[J].Kyungpook Mathe J,2008(48):93-100.
[3] XIE Zitian, ZENG Zheng. A Hilbert-type integral inequality whose kernel is a homogeneous form of degree-3[J].J Math Appl,2008(339):324-331.
[4] 杨必成.一个Hilbert型积分不等式[J].浙江大学学报:理学版,2007,34(2):121-124.
YANG Bicheng.A Hilbert-type integral inequality[J]. Journal of Zhejiang University:Science Edition,2007,34(2):121-124.
[5] 杨必成.一个具有混合核的Hilbert型积分不等式及推广[J].四川师范大学学报:自然科学版,2008,31(3):281-284.
YANG Bicheng.A Hilbert-type inequality with a mixed kernel and extensions[J].Journal of Sichuan Normal University:Natural Science,2008,31(3):281-284.
[6] 谢子填,慕容居敏.一个新的含多个参量的Hilbert型积分不等式[J].华南师范大学学报:自然科学版, 2008(2):38-42.
XIE Zitian, MU RONG Jumin.A new Hilbert type inequality with some parameters[J].Journal of South China Normal University:Natural Science Edition,2008(2):38-42.
[7] 黄臻晓.一个-4齐次核的Hilbert型积分不等式[J].华南师范大学学报:自然科学版,2009(2):20-23.
HUANG Zhenxiao.A new Hilbert-type inequality with the homogeneous kernel of-4 order[J].Journal of South China Normal University:Natural Science Edition,2009(2):20-23.
[8] XIE Zitian. A reverse Hilbert-type inequality with a best constant Factor[J].J Math Anal Appl,2008,343:1154-1160.
[9] 谢子填,曾峥.一个含有参量的Hilbert型不等式[J].湘潭大学自然科学学报,2007,29(3):24-28.
XIE Zitian, ZENG Zheng.A Hilbert-type inequality with parameters[J]. Natural Science Journal of Xiangtan University,2007,29(3):24-28.
[10] 王文杰,贺乐平,陈铁灵.参量化的Hardy-Hilbert型不等式的改进[J].湘潭大学自然科学学报,2008,30(2):12-14.
WANG Wenjie, HE Leping, CHEN Tieling.On an improvement of Hardy-Hilbert’s type inequality with some parameters[J].Natural Science Journal of Xiangtan University,2008,30(2):12-14.
[11] 匡继昌.常用不等式[M].3版.济南:山东科技出版社,2004.
Keywords: Hilbert-type integral inequality; weight function; Hölder’s inequality
【责任编辑 庄晓琼】
ANEWHILBERT-TYPEINTEGRALINEQUALITYWITHABESTCONSTANTFACTOR
ZENG Zheng1, XIE Zitian2
(1. School of Mathematics and Information, Shaoguan University, Shaoguan, Guangdong 512005, China; 2. Department of Mathematics, Zhaoqing University, Zhaoqing, Guangdong 526061, China)
By introducing some parameters and estimating the weight function, a new Hilbert-type integral inequality with a best constant factor is given. The equivalent inequality and the reverse forms are also considered.
2009-03-03
曾峥(1961—),男,广东蕉岭人,韶关学院教授、华南师范大学数学教育硕士研究生导师,主要研究方向:数学教育与不等式,Email: zz@sgu.edu.cn.
1000-5463(2010)03-0031-03
O178
A
