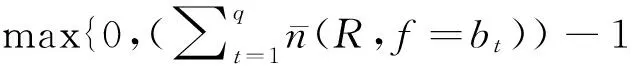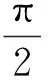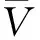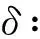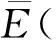关于分担集的正规定理
2010-11-18张晓梅孙道椿
张晓梅, 孙道椿
(华南师范大学数学科学学院,广东广州 510631)
关于分担集的正规定理
张晓梅, 孙道椿*
(华南师范大学数学科学学院,广东广州 510631)
用几何方法研究了更广泛的拟亚纯映射. 利用关于覆盖曲面的不等式,较简单地证明了关于分担集的正规定理. 由于亚纯函数是拟亚纯映射的特例,因此所得结论对亚纯函数均成立.
拟亚纯映射; 覆盖曲面; 正规族
设D⊂是复平面上的一个区域,是D上的一族复函数. 设V是直径为1的球面,通过球极投影与闭复平面一一对应. 设f,aV,记D;f(z)=a},若对任意f,g, 恒有则称a是的一个分担值.

关于分担值的正规定理, 有不少文章研究[1-5]. 2008年6月在绍兴召开的全国复分析会议上, 听了方明亮教授的报告, 受到启发,回来用覆盖曲面的几何方法, 对更广泛的拟亚纯映射,证明了关于分担集的正规定理, 这些定理对亚纯函数也都成立.
1 定义
定义1[6]记直径为1的Riemann球面为V,设复函数f(z)是区域D⊂V-{∞}到D′⊂V的同胚. 若
(i)在D内的任一矩形{z=x+iy;a (ii)存在K>1, 使得f(z)在D内a.e.适合 则称f是D内的K-拟共形映射. 定义3设是区域D内一族K-拟亚纯映射. 若中每一列K-拟亚纯映射{ft}恒含有在D内内闭一致收敛(按球距)的子列,即对D内任意闭集Q与中任一列K-拟亚纯映射{ft}恒含有在Q内一致收敛(按球距)子列, 则称在D内正规. 定义4设是区域D内一族K-拟亚纯映射.称为在D内等度连续, 若对D内任意闭集Q与任意ε>0,存在相应的δ>0, 使得对于任意的f以及Q上任意两点z1、z2,只要 |z1,z2|<δ,便有|f(z1),f(z2)|<ε. (D(r),f)的边界长为 引理1[11]设F0是球面V上的连通区域,其边界是q≥0个小圆(可能蜕化为点). 当q≥2时, 设任意2个小圆间的距离不小于δ(>0),则对任何有限连通的覆盖曲面F,恒有 ρ+(F)≥ρ(F0)S-25δ-3π2L, 其中ρ(F)表示F的特征数,ρ+(F)=max{ρ,0},S表示F对F0的平均覆盖次数,L是F的相对边界长度. 其中L(r)表示覆盖曲面Fr=f(|z| (1) (q-2)S-25δ-3π2L. (q-2)S(r,f)<(q-2)S(p,f) < 式(1)也成立.证毕. |f(u),f(v)|<ε. 证明由定理1, 若令r0=Re-c2/ε2 (2) 记覆盖曲面(D(r,z0),f) (r (3) 下面先证明 d(r) (4) |f(u),f(v)|≤|f(p),f(q)|≤L(r)<1. 由u,v的任意性, 得d(r) 上面第2个不等式是由于式(4); 第3个不等式是由于引理2; 第5个不等式是由于定理1. 结合式(3),就得到引理3. 定理2设是域D内的一族K-拟亚纯映射, 则在D内正规的充分必要条件是在D内等度连续. 证明充分性: 设{ft}⊂是任一序列,H={hv}⊂D是D上一个稠密的可列集.选择子序列不妨仍记为{ft},使它在H上处处收敛. 设在D等度连续. 对任意闭集Q⊂D及任意ε>0, 记Q到D的边界∂D间的距离为σ>0, 存在δ(0,σ), 使得对任意f及Q上任意两点A,B, 只要|A,B|<δ,便有 |f(A),f(B)|<ε. (5) (6) |fp(A),fq(A)|<ε. (7) |fp(B),fq(B)|< |fp(B),fp(A)|+|fp(A),fq(A)|+ |fq(A),fq(B)|<3ε. 这说明存在子序列在Q上一致收敛. |ft(At),ft(Bt)|>ε0. (8) |ft(Z),fM(Z)|<ε0/3. (9) |ft(At),ft(Bt)|<|ft(At),fM(At)|+ |fM(At),fM(Bt)|+|fM(Bt),ft(Bt)|<ε0. 这与式(8)矛盾. 定理3设是区域D⊂内的一族K-拟亚纯映射,S⊂V是的一个分担集. 若S中至少有3个点, 即3≤#(S)<∞,则在D内正规. 是有限点集. 由于亚纯函数也是K拟亚纯映射.故 推论1设是区域D⊂内的一族亚纯函数.S⊂V是的一个分担集. 若S中至少有3个点,即3≤#(S)<∞,则在D内正规. 推论2设是域D⊂V内的一族亚纯函数. 若有3个不同的分担值, 则在D内正规. 推论3设是域D⊂V内的一族K-拟亚纯映射. 若存在3个不同的复数a,b,cV, 使得对任意f,在D内恒不取a,b,c.则在D内正规. [1] 孙道椿.关于分担值的正规定则[J]. 武汉大学学报:自然科学版, 1994(3):9-12. SUN Daochun.On the normal criterion of share value[J]. Journal of Wuhan University:Natural Science Edition,1994(3):9-12. [2] FANG M L, XU Y. Normal families of holomorphic function and shared values[J].Israel J Math, 2002, 129: 125-141. [3] PANG X C. Shared values and normal families[J]. Analysis, 2002, 22:175-182. [4] LI J T, YI H X. Normal families and shared values of holomorphic function[J]. Appl Math J Chinese Univ: Ser B, 2006, 21(3):335-342. [5] 张庆德,秦春艳.亚纯函数的正规族与分担值[J]. 数学学报, 2008, 51(1):145-152. ZHANG Qingde,QIN Chunyan.Normal familles and shared values of meromorphic functions[J].Acta Mathematica Sinica, 2008,51(1):145-152. [6] 李忠, 拟共形映射及其在黎曼曲面论中的应用[M]. 北京: 科学出版社, 1988. [7] SUN Daochun,YANG Lo.Value distribution of quasiconformal mappings[J]. Complex Variables, 1997, 34:219-229. [8] 孙道椿. 拟共形映射族[J]. 华南师范大学学报:自然科学版, 2001(1):1-7. SUN Daochun.Family of quasi conformal mappings[J]. Journal of South China Normal University:Natural Science Edition,2001(1):1-7. [9] 杨乐. 值分布论及其新研究[M]. 北京:科学出版社, 1982. [10] 顾永兴. 亚纯函数的正规族[M].成都:四川教育出版社, 1991. [11] SUN Daochun. Main theorem on covering surfaces[J]. Acta Math Sci, 1994, 14(2):213-225. Keywords: quasi-meromorphic mapping; covering surface; normal family 【责任编辑 庄晓琼】 NORMALTHEOREMSONSHARESETS ZHANG Xiaomei, SUN Daochun ( School of Mathematics, South China Normal University, Guangzhou 510631, China) More extensive quasi-meromorphic mappings are discussed by the method of geometry. Normal theorems on share sets are approved simply by an inequality about covering surface.The conclusions in this paper are valid for meromorphic functions because a meromorphic function is a special case of quasi-meromorphic mapping. 2009-06-24 国家自然科学基金资助项目(10871076) 张晓梅 (1981—), 女, 湖北天门人,华南师范大学2006级博士研究生, 主要研究方向:函数论, Email:meizi_de@yahoo.com.cn;孙道椿(1943—), 男, 江西南昌人, 华南师范大学教授,博士生导师,主要研究方向:函数论,Email:sundch@scun.edu.cn. *通讯作者 1000-5463(2010)03-0015-04 O174.52 A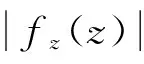



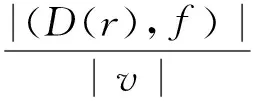
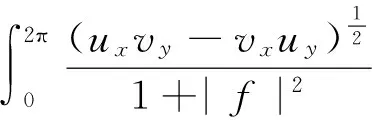
2 主要结果及证明