一类β级扩展的Bazilevic函数及其Fekete-Szegö问题
2010-11-18鲍春梅李书海
鲍春梅, 李书海
(赤峰学院数学学院,内蒙古赤峰 024001)
一类β级扩展的Bazilevic函数及其Fekete-Szegö问题
鲍春梅, 李书海
(赤峰学院数学学院,内蒙古赤峰 024001)
引进了一类β级扩展的Bazilevic函数,讨论了该类函数的Fekete-Szegö问题,给出了极值函数,并改进了一些已有的相关结果.
单叶函数; Bazilevic函数; 从属于; Fekete-Szegö不等式
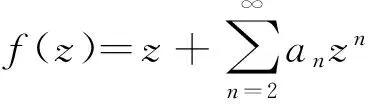

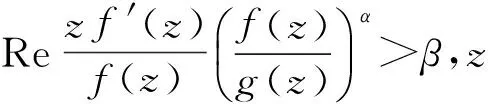
显然B(α,0,0)为熟知的Bazilevic函数类.
设f(z)与g(z)在E内解析,若存在E内满足|w(z)|≤|z|的解析函数w(z)(不必单叶),使得f(z)=g(w(z)),则称f(z)从属于g(z),记为f(z)g(z).
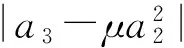

文献[2]-[4]分别研究了某些星像函数类和近于凸函数类Fekete-Szegö的问题;文献[5]研究了某Bazilevic函数子类的Fekete-Szegö问题, 文献[6]讨论了一类扩展的Bazilevic函数子类:

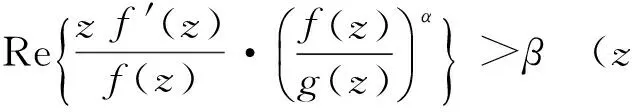

文献[6]讨论了函数类A(α,0),得到如下Fekete-Szegö不等式:
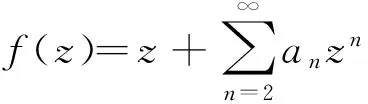
但并未给出不等式对应的极值函数.
本文的目的是讨论函数类A(α,β)的Fekete-Szegö不等式, 并得到极值函数.改进文献[6]的结果,从而给出了文献[6]没有讨论的极值函数.
为了在函数类A(α,β)中建立Fekete-Szegö不等式,需要如下2个引理:
引理1[8]设w(z)=d1z+d2z2+…在E内解析且满足|w(z)|≤|z|,则|d1|≤1,|d2|≤1-|d1|2.

下面给出本文的主要结果及其证明.
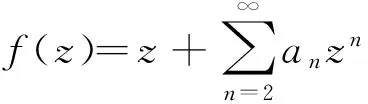
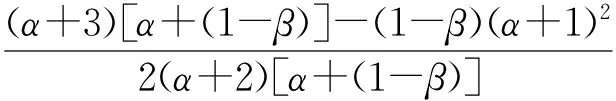

(1)
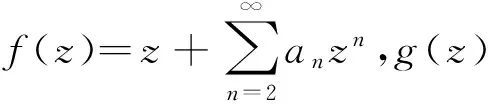
(α+1)a2=αb2+2d1(1-β),
(2)
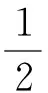
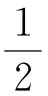
(3)
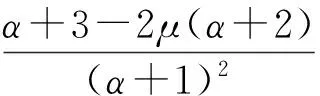
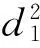
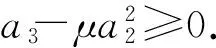

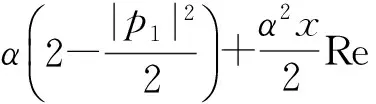
其中b2=p1=2ρeiφ,0≤ρ≤1.
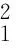
2(1-β)(1-r2)+2(1-β)(β+(1-β)x)r2cos(2θ),
其中d1=reiθ,0≤r≤1.所以
其中
ψ(x)=2α(1-ρ2)+2α2xρ2cos(2φ)+2(1-β)(1-r2)+
2(1-β)(β+(1-β)x)r2cos(2θ)+
4(1-β)αxrρcos(φ+θ).
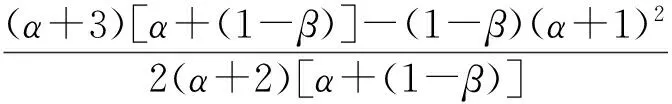
ψ(x)≤2α+2α2x+2(1-β)-
2(1-β)[(1-(β+(1-β)x)cos(2θ))r2-2αxr]=
2α+2α2x+2(1-β)-2(1-β)(1-(β+
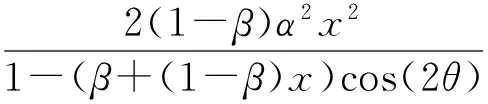
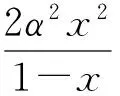
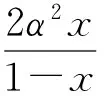
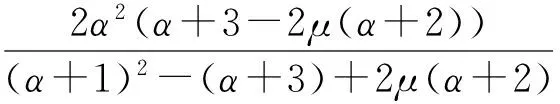
所以
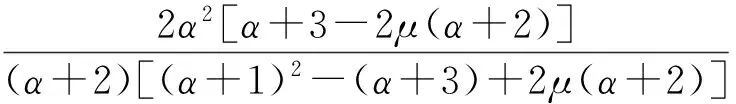
当μ1≤μ≤μ2时,不存在对应的极值函数.
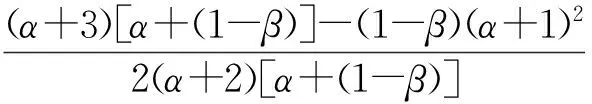
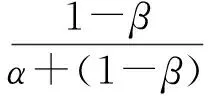
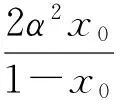
2α+2(1-β)+2α(1-β),
所以
ψ(x)=ψ(x0)+(x-x0)(2α2ρ2cos(2φ)+
2(1-β)2r2cos(2θ)+4(1-β)αrρcos(φ+θ))≤
2α+2(1-β)+2α(1-β)+
(x-x0)(2α2+2(1-β)2+4(1-β)α)=
2α+2β(1-β)+2[α+(1-β)]2x=

所以
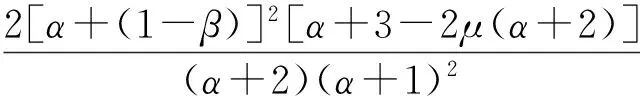
当0≤μ≤μ1时,不存在对应的极值函数.
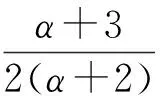
ψ(0)=2α(1-ρ2)+2(1-β)(1-r2)+
2β(1-β)r2cos(2θ)≤2α+2(1-β).
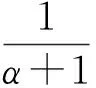
ψ(x1)-2(α+(1-β))=
-2αρ2+2α2x1ρ2cos(2φ)-
2(1-β)(1-(β+(1-β)x1)cos(2θ))×
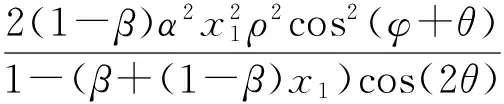
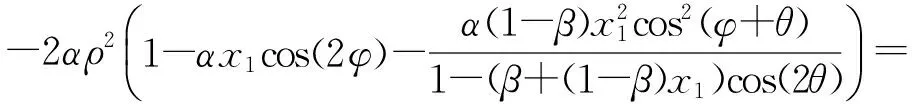
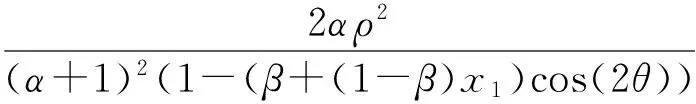
[(α+1+αcos(2φ))(α+1-(β(α+1)-
(1-β))cos(2θ))-α(1-β)cos2(φ+θ)].
令
M(β)=(α+1+αcos(2φ))(α+1-(β(α+1)-
(1-β))cos(2θ))-α(1-β)cos2(φ+θ),
则M(β)是β的一次函数,且
M(0)=2αcos2φcos2θ+αcos2θ+αcos2φ+2cos2θ+
2α2cos2φ+2αcosφcosθsinφsinθ≥
cos2θsin2φ+α2cos2φsin2θ+2αcosφcosθsinφsinθ=
(cosθsinφ+αcosφsinθ)2≥0,
M(1)=(α+1+αcos(2φ))(α+1-(α+1)cos(2θ))=
2(α+1)(1+2αcos2φ)sin2θ≥0,
故当0≤β<1时,M(β)≥0,从而ψ(x1)≤2α+2(1-β).对于0≤≤1,有
ψ(x1)=ψ(x1)+(1-)ψ(0)≤
2α+2(1-β),
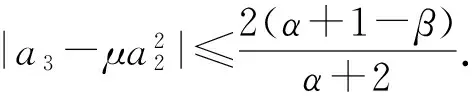
当b2=0,b3=2,d1=0,d2=1时等号成立.当α>0时,对应的极值函数为
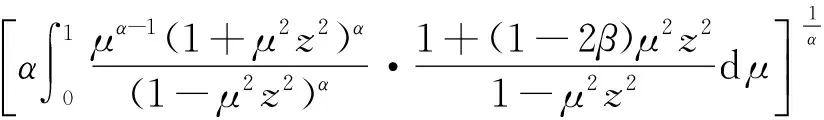
当α=0时,对应的极值函数为
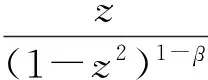
综上所述,本定理得证.
注1 定理1中β=0时,就得到定理A的改进及其对应不等式的极值函数.
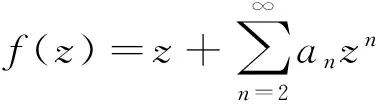
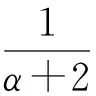
1)当0≤μ≤μ1和μ1≤μ≤μ2时,不存在对应的极值函数.
2)当μ2≤μ≤1时,存在对应的极值函数. 当α>0时,对应的极值函数为
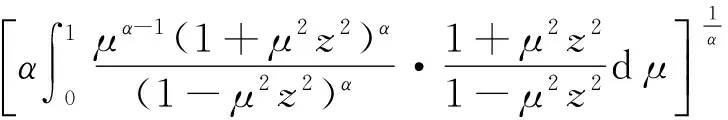
当α=0时,对应的极值函数为
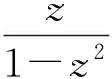
[1] FEKETE M, SZEGÖ G. Eine bermaerkung uber ungerade schlichte function[J]. London Math Soc, 1933, 8: 85-89.
[2] 刘名生. 强拟星象函数的Fekete-Szegö不等式[J]. 数学研究与评论,2000,18(1): 99-104.
LIU Mingsheng.The Fekete-Szegö inequality for strongly Quasi-Starlikefunctions[J]. Journal of Mathematics Research and Exposition, 2000,18(1):99-104.
[3] 郭栋,刘名生.关于解析函数类的Fekete-Szegö问题[J].华南师范大学学报:自然科学版,2007(2):33-38.
GUO Dong, LIU Mingsheng.On the Fekete-Szegö pro-blem for the class of analytic functions[J]. Journal of South China Normal University:Natural Science Edition, 2007(2):33-38.
[4] 李宗涛,刘名生.一类解析函数的系数泛函[J].华南师范大学学报:自然科学版,2005(3):86-91.
LI Zongtao, LIU Mingsheng.The functional of coefficients for a class of analytic functions[J]. Journal of South China Normal University:Natural Science Edition, 2005(3):86-91.
[5] GAO Chunyi. Fekete-Szegö problem for strongly Bazilevic functions[J]. Northeast Math, 1996,12(4): 469-474.
[6] 张洪光,李书海. 关于Bazilevich函数族的一个扩展及其Fekete-Szegö问题[J].纯粹数学与应用数学,2008,24(1):167-173.
ZHANG Hongguang,LI Shuhai.On an expand for a class of Bazilevich function and Fekete-Szegö problem[J].Pure and Applied Mathematics,2008,24(1):167-173.
[7] 李书海, 木林. 有关近于凸函数的一类解析函数[J]. 数学杂志,2005,25(4):428-434.
LI Shuhai,MU Lin.A class of analytic functions about Close-To-Convex functions[J].Journal of Mathema-tics, 2005,25(4):428-434.
[8] 夏道明, 张开明. 从属函数的一些不等式[J]. 数学学报,1958,8(3):408-412.
[9] 泊茂仁克 CH.单叶函数[M]. 杨维奇,译.北京:科学出版社,1987.
Keywords: univalent function; Bazilevic function; subordinate; Fekete-Szegö inequality
【责任编辑 庄晓琼】
ACLASSOFβRANKEXPANDEDBAZILEVICFUNCTIONANDFEKETE-SZEGÖPROBLEM
BAO Chunmei, LI Shuhai
(Department of Mathematics, Chifeng Colloge, Chifeng, Inner Mongolia 024001, China)
A class ofβrank expanded Bazilevic function is introduced. The Fekete-Szegö problem of this class is discused and the extremal function is given, which generalize some existing results.
2009-09-14
内蒙古自治区自然科学基金资助项目(2009MS0113);内蒙古高校科研基金资助项目(NJzy08150)
鲍春梅(1962—),女,蒙古族,内蒙古赤峰人,赤峰学院副教授,主要研究方向:复分析及其应用, Email:baochunmei19621020@126.com.
1000-5463(2010)03-0007-04
O174.51
A
