利用全等三角形巧解几何题

陈小波

几何对于很多同学来说颇为头疼.其实仔细观察你会发现，图形和题目虽然在变，但解题的方法、考察的知识点不变. 在解几何题时，有很多小诀窍可以帮助大家迅速找到解题的捷径，从而快速得出答案。下面，将通过对一道课本例题的变式探究，讲解如何利用全等三角形巧解几何题.

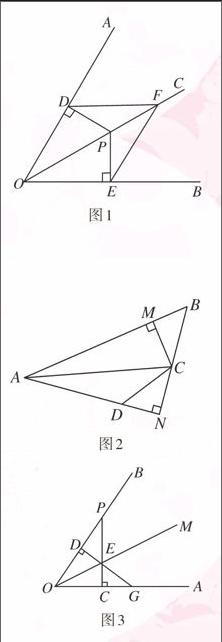
【例1】如图1，OC是∠AOB的平分线，P是OC上的一点，PD⊥OA， PE⊥OB， 垂足分别为D，E. F是OC上的另一点，连接DF，EF .求证：DF=EF.（人教版八年级上册第51页第5题）

【点拨】根据以往经验，要求证DF= EF ，可通过证这两条线段所在的两个三角形全等，但根据已知条件只能找到两个全等条件，还缺少第三个条件，故寻找第三个条件是解决问题的关键.

【解题方法】

方法1：先证△OPD≌△OPE，得OD=OE，这就是证明△ODF≌△OEF的第三个条件.

方法2：先证△OPD≌△OPE，得∠DPO=∠EPO，从而它们的邻补角∠DPF=∠EPF，这就是证明△DPF≌△EPF的第三个条件.

【总结】想要证明两个三角形全等而条件不够时，可先证其他三角形全等，得到对应边或对应角相等，再把这些作为证明所求的三角形全等的条件.

探究一： 已知条件不变，结论改变

【变式1】如图2，已知AC平分∠BAN，CM⊥AB于点M，CN⊥AN于点N，且BM=DN，求∠ADC与∠ABC的关系.

【点拨】这道题求的是∠ADC与∠ABC的关系，与之前证线段相等或证角相等不同。仔细观察图形，可以发现有一对三角形△CDN和△CBM全等，从而把对应角∠ABC转移为∠CDN，而∠CDN与∠ADC是互补关系，因此得出∠ADC与∠ABC的关系.证明略.

【变式2】如图3，小强在∠AOB的平分线OM上任意取一点E，过点E分别作OA，OB的垂线EC，ED，垂足为C，D.当他把EC，ED反向延长，分别与OB，OA相交于点P，G后，他认为EP=EG，你认为他的看法正确吗？请说明理由.

【点拨】这道题要证明的是两条线段的关系，同样观察图形可知，可能会有三角形全等. 把这两条线段分别归入两个三角形中，再证明这两个三角形是否全等，从而可证小强的结论是否正确.本题证明过程相对简单，略.

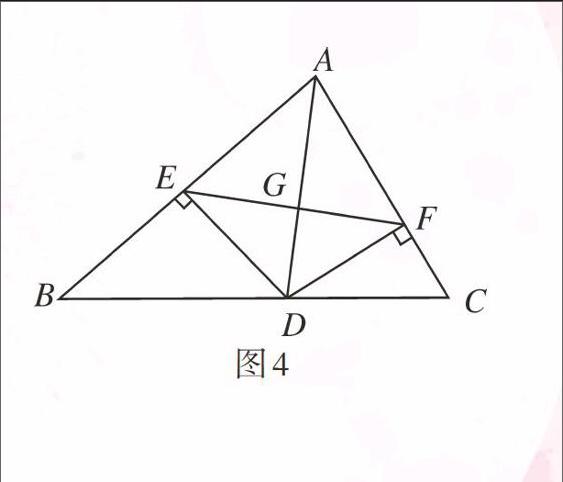
【变式3】如图4，AD是△ABC中∠BAC的角平分线，DE⊥AB，DF⊥AC，垂足分别是点E，F，连接EF交AD于点G.请问AD与EF垂直吗？证明你的结论.

【点拨】这道题可用不同的方法来求解.

解题方法1：先证△AED≌△AFD，得AE=AF，再证△AEG≌△AFG，从而得到∠AGE=∠AGF=90°.

解题方法2：先证AD是∠EDF的平分线，根据角平分线的性质，得AE=AF，再证△AEG≌ △AFG，从而得到∠AGE=∠AGF=90°.

证明：∵DE⊥AB，DF⊥AC，

∴∠EAD+∠EDA=90°， ∠FAD+∠FDA=90°

∵ AD是△ABC中∠BAC的角平分线

∴∠EAD=∠FAD

∴∠EDA=∠FDA

∴ AD是∠EDF的角平分线

∵ AE⊥DE，AF⊥DF

∴ AE=AF

在△AEG和 △AFG中，AE=AF，∠EAG=∠FAG，AG=AG

∴ △AEG≌ △AFG （SAS）

∴∠AGE=∠AGF=90°

∴ AD⊥EF

探究二： 图形延伸的变式题

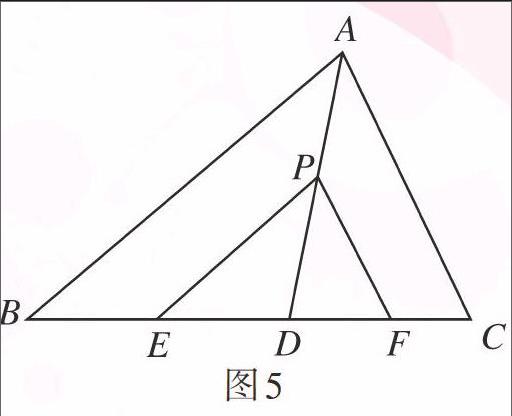
【变式1】如图5，在△ABC中，AD是∠BAC的角平分线，P是AD上的一点，PE∥AB，交BC于点E，PF∥AC，交BC于点F.求证：点D到PE和PF的距离相等.

【点拨】欲证点D到PE和PF的距离相等，要先证点D在∠EPF的平分线上.

证明： ∵AD是∠BAC的平分线

∴∠BAD=∠CAD

∵PE//AB ，PF//AC，

∴∠BAD=∠EPD，∠CAD=∠FPD

∴∠EPD=∠FPD

∴PD是∠EPF的平分线

∴点D到PE和PF的距离相等.

【变式2】如图6，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE=AF.

求证：（1）PE=PF；

（2）点P在∠BAC的平分线上.

证明：连接AP

（1）∵PE⊥AB，PF⊥AC

∴△APE和△APF是直角三角形

在Rt△APE和Rt△APF中，

AP=AP

AE=AF

∴△APE≌△APF （HL）

∴PE=PF

（2）据（1）得PE=PF

∵PE⊥AB，PF⊥AC

∴点P在∠BAC的平分线上

探究三： 更复杂的图形延伸探究

【变式1】（1）如图7，在△ABC中，∠ACB是直角，∠B=60°，∠BAC与∠BCA的角平分线AD，CE相交于点F.请你判断FE与FD之间的数量关系，并说明理由.

【点拨】观察图形可知，图中没有现成的全等三角形，需要作辅助线构造一对全等三角形来解决问题.根据角平分线的性质，过点F作FG⊥AB，FH⊥BC，再证明△EGF≌ △DHF，从而得到FE=FD.

解：FE=FD

理由：如图8，过点F作FG⊥AB，FH⊥BC，FM⊥AC，分别交AB，BC，AC于点G，H，M.

∵F为∠BAC，∠BCA的平分线的交点

∴∠EAF=∠CAF=15°，∠ECA=∠ECB=45°，FG=FM=FH

∴∠GEF=∠EAC+∠ECA=30°+45°=75°

∠HDF=∠BAD+∠ABD=15°+60°=75°

∴∠HDF=∠GEF

∵∠FHD=∠FGE=90°

∴△DFH≌△EFG

∴ FD=FE

（2）如图9，在△ABC中，如果∠ACB不是直角，而（1）中的其他条件不变，那么在（1）中所得结论是否依然成立？若成立，请证明；若不成立，请说明理由.

解：结论FE=FD 仍然成立.

理由：如图10，过点F作FG⊥AB，FH⊥BC， FM⊥AC

∵∠B=60°，且AD，CE分别是∠BAC，∠BCA的平分线

∴∠CAD+∠ACE=60°，FG=FH=FM

∴∠GEF=∠BAD+∠CAD+∠ACE=60°+∠BAD

∵∠HDF=∠B+∠BAD=60°+∠BAD

∴∠GEF=∠HDF

∵∠FGE=∠FHD=90°

∴△EGF≌△DHF

∴ FE=FD

以上的几道变式题，反复利用了角平分线的性质和三角形全等的判定这几个定理.虽然图形在变，但解题的方法几乎都是一样的，都通过证三角形全等来求问题的答案.同学们以后在解答这类题目时，一定要细心观察图形，如果能找出可能全等的三角形或作辅助线构造一对全等三角形，很多几何题都能迎刃而解.