深井爆破振动小波分析及其应用
2010-11-17王群峰,董凯程
深井爆破振动小波分析及其应用
王群峰1,董凯程2
(1.安徽铜都铜业股份有限公司冬瓜山铜矿, 安徽铜陵市 244000;2.中南大学资源与安全工程学院; 湖南长沙 410083)
根据小波分析理论,对深井爆破振动信号进行频带划分,给出不同频率带上爆破振动的相对能量分布和振动强度的时间变化规律,并分析总结深井爆破振动衰减规律。与传统Fourier变换基础上的频谱分析方法相比,基于小波变换的爆破振动时频特征分析可以给出更为准确的细节信息。研究成果对研究深井爆破振动具有重要意义。
爆破振动;小波变换;衰减规律;深井开采
1 爆破振动信号小波分析原理[1]
在小波多分辨分析条件下,爆破振动信号s(t)满足如下分层分解关系:
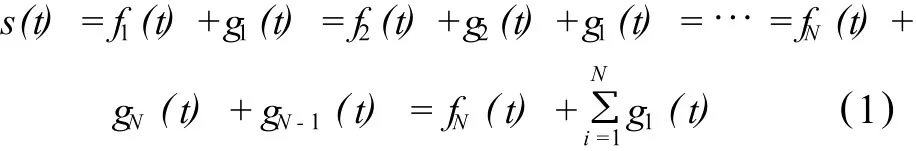
为了表达简洁,令g0(t)=fN(t),则(1)可以表达为:

式中,f表示为爆破振动信号s(t)小波分解的低频部分,g表示为爆破振动信号s(t)小波分解的高频部分,下标表示所对应的分解层次。
小波多分辨分析可以将爆破振动信号分解到不同的频带上,在每个频带上的爆破振动分量仍然是关于时间变化的信号。因此,爆破振动信号通过离散小波变换的分层分解,可以对不同频带范围内爆破振动分量的时间变化规律加以分析。
如果将爆破振动信号s(t)进行层次为N的小波分解和重构,根据小波函数的正交性式(2)可得信号的总能量E为:
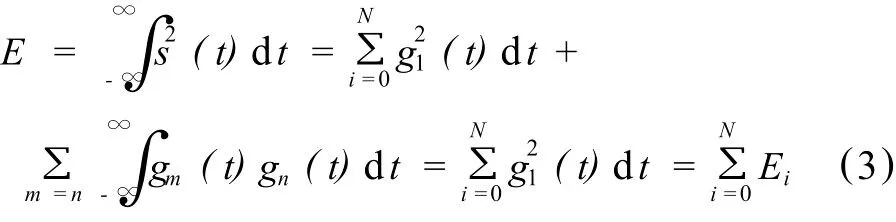
式中,Ei为爆破振动分量的小波频带能量,即:

由此可知,不同频带爆破振动分量的相对能量分布为:

由于爆破振动检测时,信号的采样点数总是有限的。若采样点数为M,可将式(3)表示为:

式中aN(n)为爆破振动信号小波分解的近似部分,di(n)为爆破振动信号小波分解的细节部分。
由式(6)可得,各频带爆破振动分量的小波频带能量为:

2 深井爆破振动信号的小波时频特征分析
2.1 爆破振动信号小波分解
对该深井爆破振动信号进行小波时频特征分析,用db8小波基对该信号进行尺度为7的小波分解[1~3],可获得8个频带的小波分解系数。根据香农(Shannon)采样定理[4],8个频带宽度分别为:0~7.8125,7.8125~15.625,15.625~31.25,31.25~62.5,62.5~125,125~250,250~500,500~1000 Hz。利用小波分析原理,将图1的爆破振动原始信号分解以后再进行重构,得到各个频带的爆破振动时程曲线,典型的时程曲线如图2~4所示。
根据式(1)~式(8)利用MATLAB语言编制计算程序,可获得该爆破振动小波分析的总能量、各频带爆破振动的最大PPV、各频带爆破振动小波频带能量及其分布,见表1。

图1 爆破振动原始信号

图2 15.625~31.25Hz爆破振动分量

表1 爆破振动信号的频带参数
2.2 爆破振动信号小波变换特征分析
由图5可以看出该爆破振动主频在140~160 Hz,即该爆破振动的峰值质点振动速度(PPV)所在频率为140~160Hz,也正处在125~250Hz频带之间,也就是说爆破振动PPV的大小可以由小波频带能量的大小来反映。由图4也可以看出,此频带爆破振动最大PPV高于其他频带。因此,小波频带能量可以基本反映爆破振动的强度。

图3 31.25~62.5Hz爆破振动分量
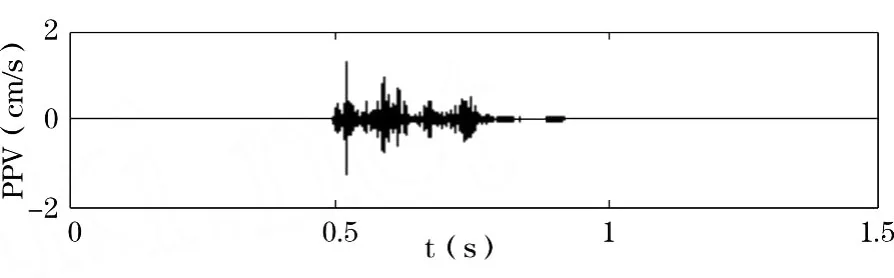
图4 125~250Hz爆破振动分量
与传统的Fourier变换相比,小波分析能给出爆破振动信号的时频分布特征,更能反应爆破振动的非平稳性,更好的满足爆破振动非平稳随机性特征分析的要求。爆破振动信号小波分析的频带能量,可以同时反应爆破振动3要素(振动强度、频率和持续时间)的作用影响。与峰值质点振动速度(PPV)单一反映爆破振动的强度相比,小波频带能量可以更精细、更准确和更全面地反映爆破振动的作用影响[1]。

图5 爆破振动信号SPWV图
3 深井爆破振动衰减规律分析
深井爆破振动衰减规律研究对深井爆破振动效应分析具有重要意义。基于上述小波分析理论对某深井不同中段爆破振动进行测试分析,将爆破振动原始信号进行分解重构,得出各中段振动信号主频带速度时程图。就爆破振动主频带频率分布、主频带宽及作用时间进行分析,以此研究深井爆破振动随高度的衰减规律。
在信号的低、中频带,振动分量衰减缓慢,振动持续时间较长,频带PPV越大,小波频带能量就越大;在信号的高频带,尽管高频带振动分量的频带PPV较大,由于高频带振动分量的衰减较快,振动持续时间较短,小波频带能量也就较小。因此小波频带能量可以反映爆破振动时间的作用影响。
从图6~8可以看出,随着埋深的不断增大,爆破振动主频不断增大,且爆破振动信号能量主要集中频带也越来越宽;随着埋深的不断增大,爆破振动主频带作用时间也不断减小,也就是说深井爆破振动主频作用时间相对较短,爆破振动作用更加瞬态化,但其爆破振动作用却更具有破坏性[5,6]。
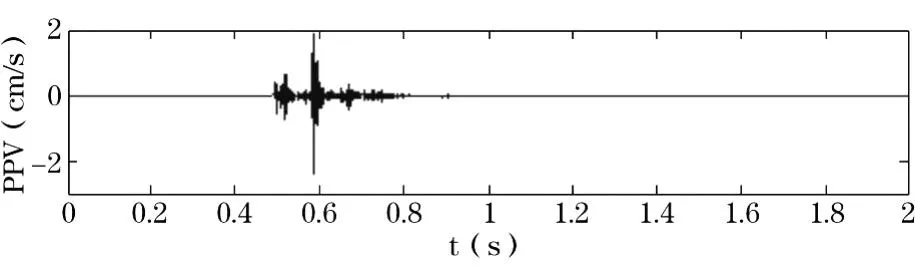
图6 825m中段爆破振动主频带(125~250Hz)

图7 760m中段爆破振动主频带(31.25~62.5Hz)
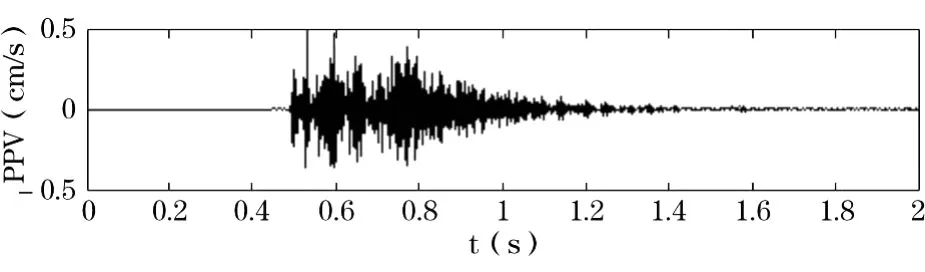
图8 40m中段爆破振动主频带(15.625~31.25Hz)
4 结 论
(1)基于小波变换的深井爆破振动信号分析方法,可以同时反映爆破振动3要素(振动的强度、频率和持续时间),克服了传统Fourier变换的不足,能更好的表征爆破振动信号特征。
(2)随着埋深的增大,爆破振动主频带分布、主频带宽及作用时间在呈现规律性变化,为深井爆破振动研究提供理论依据。
(3)虽然应用该方法对深井爆破振动效应进行了理论研究,但其灾害的控制方法仍需要进一步探索。
[1]中国生.基于小波变换爆破振动分析的应用基础研究[D].长沙:中南大学,2006.
[2]葛哲学,等.小波分析理论与MATLABR2007实现[M].北京:电子工业出版社,2007.
[3]陈志奎.工程信号处理中的小波基和小波变换分析仪系统研究[D].重庆:重庆大学,1998.
[4]邹云屏,李 潇,等.信号变化与处理[M].武汉:华中理工大学出版社,1993:8~12.
[5]王恒福.浅埋隧道掘进爆破振动效应及其控制研究[D].长沙:中南大学,2008.
[6]凌同华,等.爆破震动灾害主动控制方法研究[J].岩土力学,2007,28(7):1440~1442.
2009-10-12)
王群峰(1973-),男,安徽人,采矿工程师,主要从事采矿技术工作。
