自然电位和双侧向 /双感应数据在2D地层中的联合反演

2010-11-16编译兰艳大庆钻探工程公司测井一公司

石油石化节能 2010年1期

关键词：矿化度侧向测井

编译:兰艳 (大庆钻探工程公司测井一公司)

审校:赵平 (大庆钻探工程公司测井一公司)

自然电位和双侧向 /双感应数据在2D地层中的联合反演

编译:兰艳 (大庆钻探工程公司测井一公司)

审校:赵平 (大庆钻探工程公司测井一公司)

当渗透性地层采用水基泥浆钻开后,如果泥浆矿化度与地层水矿化度不同,那么在沿井壁、层边界和侵入带边界就会形成偶极层。这种偶极层在井眼中可以产生自然电位 (SP)。因此,通常使用自然电位曲线来划分渗透性地层,并计算地层水电阻率。和其他测井方法一样,自然电位测井也受测井环境如侵入、围岩、井眼等条件的影响,虽然这些环境因素不影响划分渗透性地层,但却影响地层水电阻率的计算,这是因为计算地层水电阻率需要由自然电位推导出的静自然电位 (SSP)。为了校正这些影响因素,做了很多校正图版,然而,在非常复杂的测井环境中,这些图版并不能完全校正上述提及的影响因素。本文提出了一种由自然电位和双侧向/双感应测井数据计算静自然电位的联合反演方法。首先,层界和渗透层可以用自然电位、自然伽马和电阻率曲线划分。其次,可以用双侧向/双感应测井数据来推导地层电阻率,在渗透层可以反推三个参数,即侵入带电阻率、原状地层电阻率和侵入半径。在非渗透层,仅反推地层电阻率。最后应用反演得到地层电阻率,即用SP数据反演SSP。SSP反演是点源SSP的反演,而不是偶极层内电位的反演,这些点源位于层边界和侵入带边界、层边界和井壁之间的接点处。由于这种反演方法不必考虑边界的形状,反演也相对变得简单。基于该方法,开发了一种反演准则,这个准则在非洲和我国的油田通常被用来反演SSP和计算地层水电阻率。例如,对于一个纯砂层,厚度为7 m,最大SP为70 mV,反演得到 SSP为83.2 mV,且由SSP计算的地层水矿化度为2 416×10-6,这个值与通过地层水分析得到的地层水矿化度为2 330×10-6非常接近。

自然电位双侧向双感应2D地层联合反演

1 引言

当泥浆滤液和地层水的矿化度不同时,就会产生自然电位。在水基泥浆情况下,SP通常用来划分渗透层、计算地层水矿化度或地层水电阻率。地层水电阻率通常是计算地层含水饱和度的关健参数之一。

获得地层水电阻率有以下方法:进行地层水测试直接进行测量,或根据SP测井数据进行计算。其中第二种方法是目前可利用的最经济的方法。同其他测井方法 (如电阻率测井)一样,SP测井也受井眼环境条件的影响,如井眼、侵入和围岩的影响。为了搞清这些影响因素,科学家们进行了数值模拟和实验室研究 (Taherian,R.等人,1992;Zhang,G.J.等人,1999)。为了校正这些影响因素,测井分析家们使用SP图版来计算地层水电阻率,但这些图版仅适用于一些有限的地层条件,如无侵入或台阶状侵入,然而实际地层通常比SP图版描述的地层更复杂。

本文将描述一种联合反演方法。首先用SP、Gr(伽马射线)曲线划分渗透层;其次用电阻率测井划分地层边界;再次用双侧向/双感应测井数据反演地层电阻率分布,包括地层真电阻率、侵入带电阻率和侵入半径。最后由反演得到的地层电阻率分布反演SSP,SSP可用来计算地层水矿化度和地层水电阻率。

2 正演模型理论

等效源——当渗透层被钻开后,在侵入带和原状地层之间的边界、渗透层和围岩之间的边界以及井壁和围岩之间的边界都会形成带电偶极层。在图1中,通过这些偶极层的电位降可以用ε1～ε7来表示。使用闭合带电偶极层可使图1中的等效源简单化。

如图2所示,用电位ε和闭合区域D表示一个闭合带电偶极层,则由偶极层产生的电位可表达为:

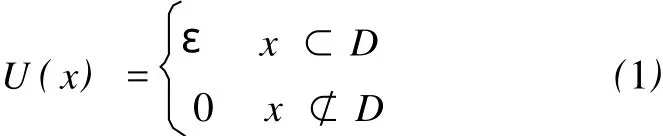
利用图2中所定义的带电偶极层的概念,图1所示的电位可以简化为如图3所示。图3中右方弧形线位于无限远处,因此在井眼中SP曲线上 -ε1的值是0,且 -ε3和 -ε6的值为一常数。忽略 -ε3和-ε6对自然电位的影响,因为仅使用了自然电位曲线相对基线值的差异。在这种假设条件下,设ε2=ε3=ε5=ε6,则图3可以简化成图4。图4中SSP可以定义为:

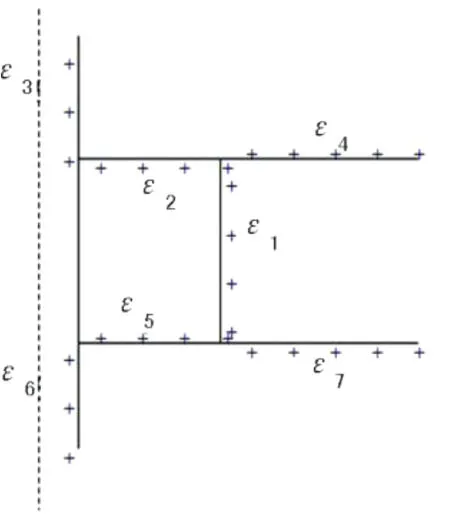
图1 边界上的带电偶极层

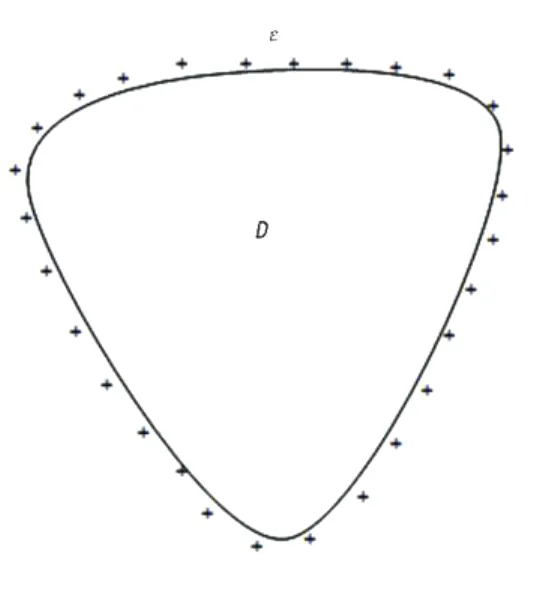
图2 闭合带电偶极层

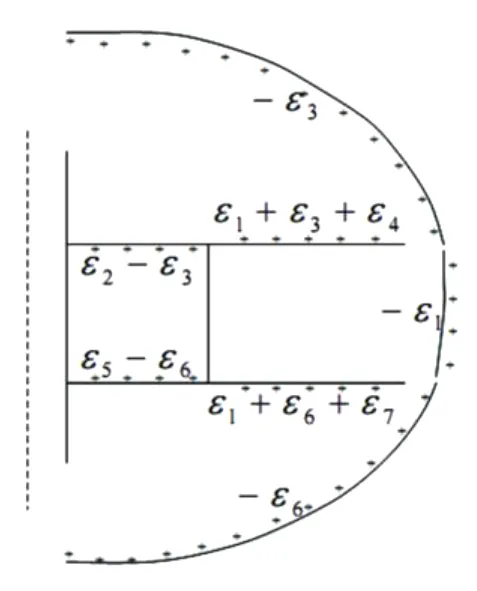
图3 图1的等效源图

如图4所示,产生SP的源可以等效成层边界上两个带电偶极层,从层边界之间和侵入带边界之间的接点处到无限远处。

图4中所示的源可以简化成位于接点处的点源,其控制函数表达式为:

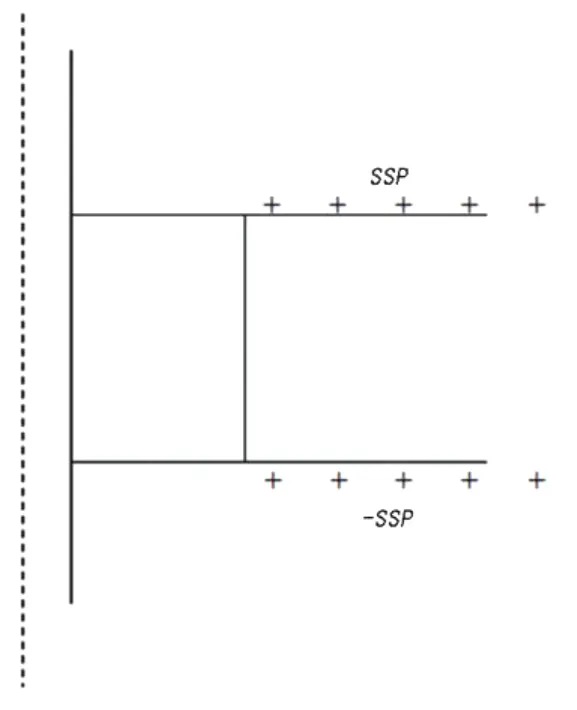
图4 图3的等效源图

3 正演模拟结果

使用有限元法 (FEM)计算SP曲线。模拟结果如图5所示。在图5中,SP-c/SSP是模拟方法的SP和SSP的比值,SP-an/SSP是分析计算方法的SP和SSP的比值。从图中可以看出两个数值结果匹配,且证实了正演模拟方法的正确性。

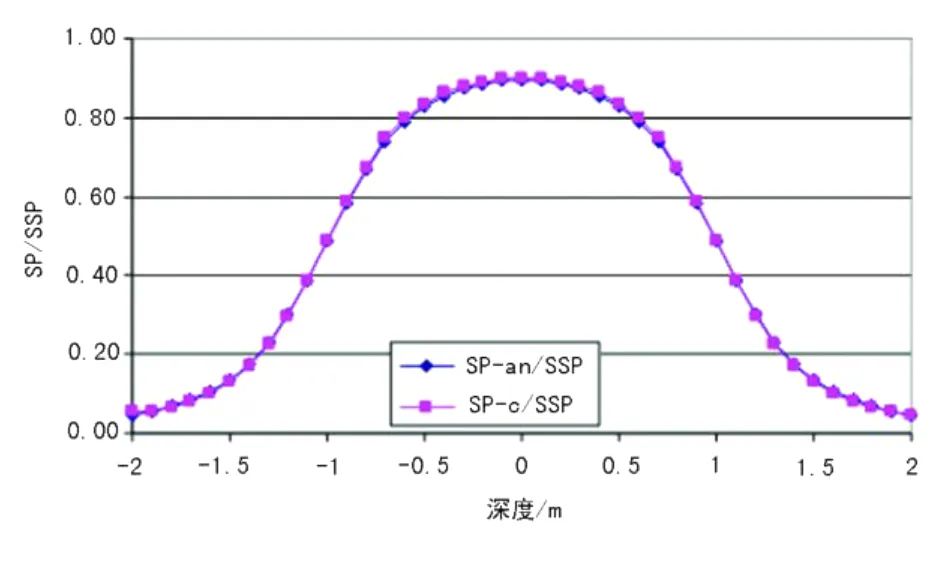
图5 解析法和数值模拟法对比

4 反演方法

使用MLM(Marquardt-Levenberg Method)反演地层电阻率分布和SSP(Marquardt,1963)。

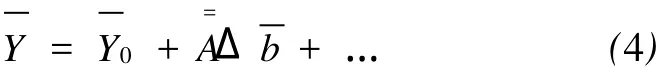
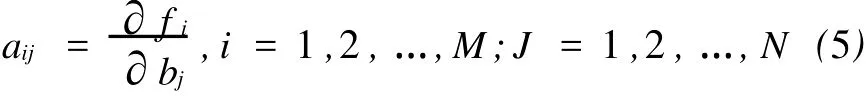
若忽略公式中的高阶项,则有

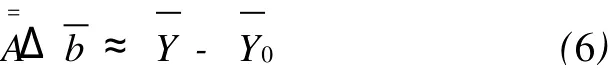
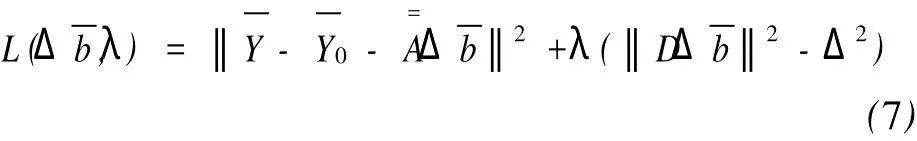
式中λ是拉格朗日因子。对于某一固定的点,拉格朗日公式需要一个必要条件,即

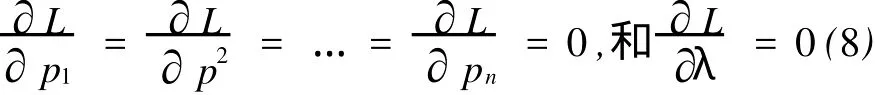
因此,求方程 (7)中提到的导数,并整理方程,得出以下方程 (Marquardt,1963):

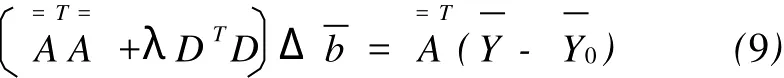
5 反演过程

反演过程可分为如下几步:

◇用SP和 Gr划分渗透层;

◇用双侧向/双感应曲线确定地层电阻率边界;

◇给定地层电阻率分布和SSP初始值;

◇在渗透性地层中进行地层电阻率分布、地层真电阻率 (Rt)、侵入带电阻率 (Rxo)、侵入半径(Ri)的反演,及在非渗透层中进行 Rt的反演;

◇用地层电阻率分布和SP测井曲线进行SSP的反演。

6 用方差曲线确定边界位置

假定图6中所示曲线,选择窗值 N,若 N=5,测点 i-2、i-1、i,i+1、i+2。在这个窗值中,首先用方程 (10)计算曲线平均值:

式中,Raj是第j个深度点上的视电阻率曲线值。接着,用公式 (11)计算第i深度点的方差:

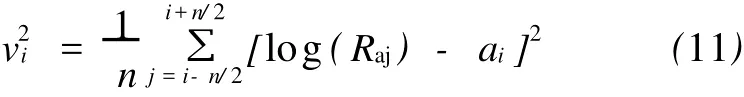
然后被指定给第i个点,由此可以得到一个方差曲线,它可以用来确定地层边界位置。

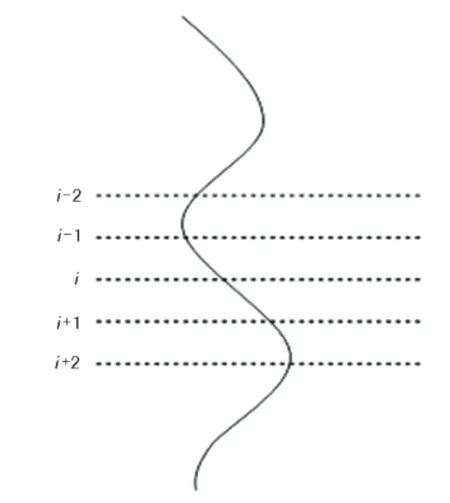
图6 视电阻率测井曲线

7 确定电阻率分布的初始值

假设感应测井响应可以表达为:

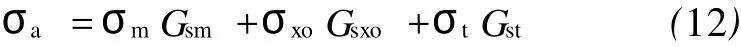
式中,Gsm、Gsxo和Gst分别代表井眼、侵入带和原状地层的Doll积分因子;σm、σxo和σt分别代表泥浆、侵入带和原状地层的地层电导率,且 Gsm+Gsxo+Gst=1。

假设双侧向测井的响应可以表示为:

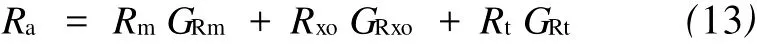
式中,GRm、GRxo和 GRt分别代表有限元法模拟的井眼、侵入带和原状地层的积分因子;Rm、Rxo和 Rt分别代表泥浆、侵入带和原状地层的电阻率,且

利用公式 (12)表达的双感应测井曲线,公式(13)表达的双侧向、球型聚焦、微球聚焦测井曲线及视层无边界,在渗透层当中可推导出 Rt、Rxo和 Ri,在非渗透层中可推导出 Rt。推导出的电阻率分布可作为反演的初始值。

8 确定SSP的初始值

本文中,认为产生SP的源是位于层边界和侵入带边界的接点处的点源,而不是在偶极层内部,点源的值是SSP。因此,在每一个渗透层,SSP可以直接推导出来。

9 反演结论

图7为我国西部某油田反演电阻率分布图,RT和R X(第三道)分别是反演出的原状地层电阻率和冲洗带电阻率 (两者来自双侧向测井数据)。So′和So分别代表从测井曲线数据直接计算的含油饱和度和由反演处的Rt计算的含油饱和度。某井渗透层 (＊180.5～＊189 m)上部,两种方法计算的含油饱和度分别为67%(So′)和81%(So);层中部,计算的含油饱和度分别为65%(So′)和71%(So)。这个油田的测井分析家认为,比起So′,So与现场试验结果更接近。

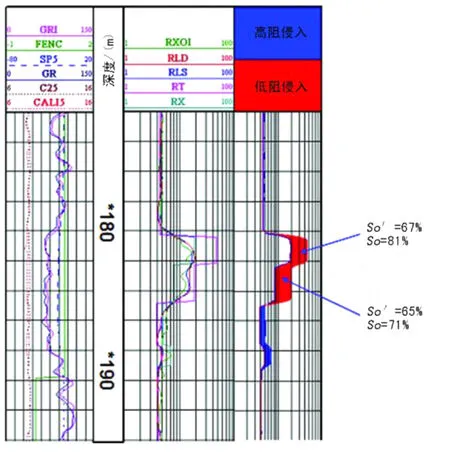
图7 我国西部某油田反演结果图例

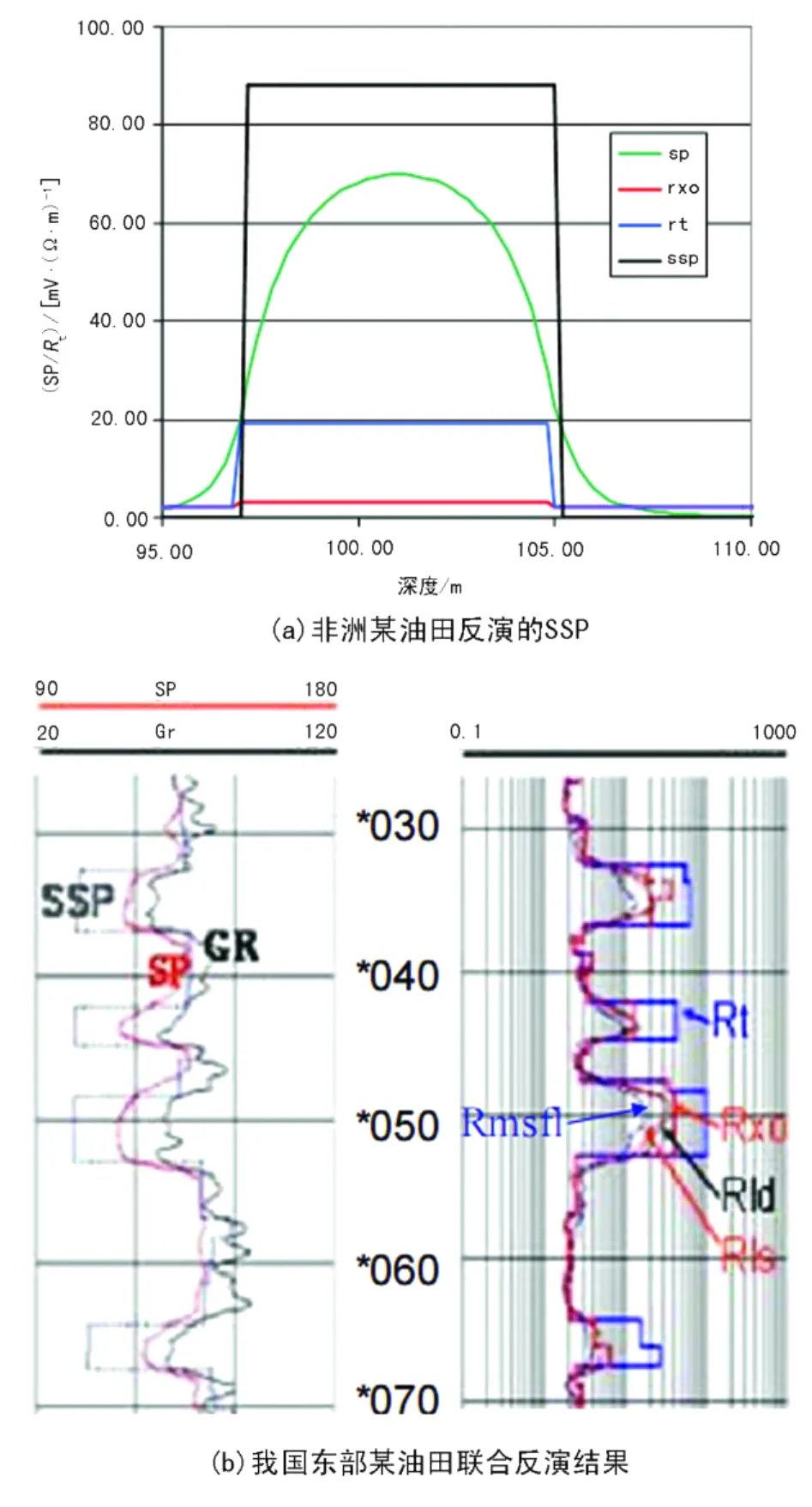
图8

图8(a)是非洲某油田反演结果图例。在一个纯砂岩储层,SP值为70 mV,(层中间)层厚7 m,反演的 Rt=19.3Ω·m、Rxo=3Ω·m,Ri=17 in(1 in=25.4 mm)。利用反演法则,反演SSP=83.2 mV。利用SSP,计算地层水矿化度为2 416 ppm(1 ppm=10-6),这个值与在实验室内根据地层水分析获得的矿化度为2330 ppm很接近。由SSP计算的地层水电阻率为0.98Ω·m

图8(b)为我国东部某油田的联合反演结果图例。＊020～＊070 m,根据SP曲线划分出4个渗透层。在渗透层中可反演 Rt、Rxo、Ri,在非渗透层中可反演 Rt,测井曲线 Rmsfl、Rls、Rld,表明 4个层为低阻侵入,这与Rt大于Rxo相一致。利用反演出的地层电阻率分布和SP数据,运用本文所提出的反演方法可反演得到SSP。图8(b)表明SSP曲线与SP曲线在渗透层分离,在非渗透层接近。