斜井泥岩声波速度各向异性校正新方法研究

乔悦东（中海石油研究总院，北京100027）

孙建孟，耿尊博（中国石油大学（华东）地球资源与信息学院，山东 东营257061）

斜井泥岩声波速度各向异性校正新方法研究

乔悦东（中海石油研究总院，北京100027）

孙建孟，耿尊博（中国石油大学（华东）地球资源与信息学院，山东 东营257061）

斜井中测量到的声波记录了泥岩中纵波速度的各向异性，进行泥岩速度各向异性校正需要确定泥岩的汤姆森系数，传统上汤姆森系数通过泥岩实验测量或应用地震资料经具有垂直对称轴的横向各向同性（VTI）介质非双曲时差速度反演获得。针对这两种方法存在的困难，提出在多口斜井声波资料地层对比的基础上，选取同一层位多口井的测井声波资料，以椭圆方程作为反演模型，采用最小二乘法确定汤姆森系数的新方法，由此实现斜井泥岩声波速度各向异性校正。该方法在渤中地区的实际应用表明，大斜度井中实测声波速度与地层真正垂向速度的差异巨大，校正量达到了20%～30%，为斜井地震正、反演提供了精确的声波速度，提高了斜井测井刻度在地震实际应用中的精度。

斜井；测井泥岩声波速度；各向异性；校正；汤姆森系数

当斜井井斜角超过20°时，随着井斜角的增大，测井得到的泥岩声波速度显著增加［1］，这一变化对测井刻度地震产生重要影响。由于声波测井仪器是在平行于钻孔的情况下进行声波测量，所以在斜井中测量到的声波记录了泥岩中纵波速度的各向异性。在斜井中由于垂直声波速度到水平声波速度的各向异性可以达到30%甚至更多，用测井数据直接生成合成地震记录或用于地震正、反演会产生很多问题。因此，为了提高测井刻度地震的精度，需要对斜井中的声波测井资料进行各向异性校正。

按照Hornby的椭圆方程理论［2］，进行泥岩速度各向异性校正需确定泥岩的汤姆森系数，传统上汤姆森系数是通过泥岩实验测量［3］，或是应用地震资料经具有垂直对称轴的横向各向同性（VTI）介质正常时差速度反演获得［4］。但实验室条件下求取各向异性参数主要是针对某些典型的具有代表意义的泥岩进行研究，实际地下的地层具有很复杂的矿物组分和排列结构［5～8］；反演理论是建立在弱各向异性假设条件下的，当各向异性强度很大的时候，该理论基础上反演得到的参数会有很大的偏差。针对上述传统方法求取汤姆森系数存在的问题，笔者提出了在多口斜井声波测井资料地层对比的基础上，选取同一层位多口井的测井声波资料，以椭圆方程作为反演模型，采用最小二乘法确定汤姆森系数的新方法，实现斜井泥岩速度各向异性的校正，为斜井测井刻度地震提供准确的声波速度。

1 校正方法

1.1 汤姆森系数的定义

横向各向同性的混合介质有5个独立的弹性常量。弹性强度张量C可以用Voigt符号表示：

式中，C11为面内压缩模量，kg/（m·s2）；C13为一个控制波前面形状的重要常量，kg/（m·s2）；C33为侧向压缩模量，kg/（m·s2）；C44为侧向剪切模量，kg/（m·s2）；C66为面内剪切模量，kg/（m·s2）；C12＝C11－2C66，kg/（m·s2）。

根据测量到的声波速度可得出如下表达式：

式中，ρ为体积密度，kg/m3，并假设它关于纵轴对称；VPH和VSH为水平方向上的P波和S波速度，m/s；VPV和VSV是垂直方向上的P波和S波速度，m/s。

C13的解较为复杂，但是对于45°的相位传播，C13可表示为：

式中，V45为相对于对称轴倾角为45°时的P波和S波的实测速度；对于P波的速度测量取m＝－1，对于S波的速度测量取m＝1。

对于各向异性的对比分析，根据2个弹性模量和3个各向异性参数可重新定义上面5个弹性常量［9］。汤姆森把这3个各向异性参数定义为ε（P波的各向异性因子）、γ（S波的各向异性因子）和δ（临界因子，它与P波和相对于对称轴倾角为45°时的S波的波前面有关）：

这3个各向异性参数有使方程简化、无量纲、在各向同性变差时减小到零的特点。笔者进行泥岩速度各向异性研究，只讨论ε。

1.2 反演模型的建立

国外，Brian E.Hornby等人采用一种利用多种不同倾斜角的刻度井群的迭代反演方法来反演泥岩的各向异性参数［2，10］，其方法是使模型化的纵波群速度波前面与测量数据之间的均方根误差最小。均方根误差W被定义为：

式中，N为测量的独立信号的总数；VPθm为倾斜角为θ的井的测量速度，m/s；VPθe为模型化的纵波群速度，m/s。

图1 各向异性地层中群速度波前面形态示意图

图1是各向异性地层中群速度波前面形态示意图。利用式（10）可以反演得到各向异性地层中群速度波前面，为简化计算，可将其简化为椭圆形曲线。假设P波群速度波前面为椭圆，结合式（2）、式（3）和式（7）得椭圆方程为：

直线方程为：

由式（7）、式（12）及倾斜角为θ处的声波速度VPθ可得：

式（13）两边平方，整理可得：

由于倾斜角θ和该倾斜角测得的声波速度VPθ为已知，上述方程中的系数便可知。从不同的井、不同的深度点分别取对应一个倾斜角的声波测井数据值代入式（15），应用最小二乘法求解超定线性方程组，可求得x1和x2，继而求得各向异性系数。

1.3 汤姆森系数的求取

从不同的井、不同的深度点分别取对应一个井斜角的声波测井数据代入式（15）中，得到m组方程：

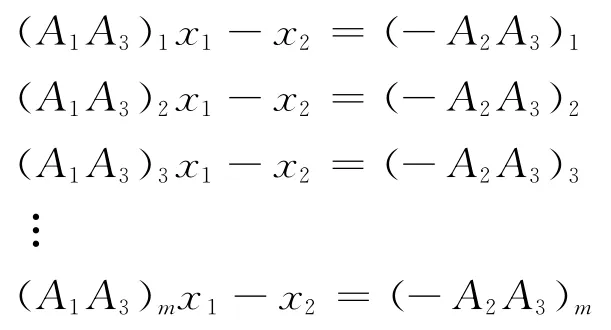
从上述方程组中提取系数矩阵：

其中，A为m×2维的矩阵，B为m×1维矩阵。

因此，可得：AX＝B

系数矩阵A为列线性无关向量，因此，可以用House－holder变化方法对其进行分解，然后解方程组得x1、x2。则可得汤姆森系数ε（P波的各向异性因子）：

2 应用效果分析

以渤中区块的4口倾斜井为例进行分析与讨论。首先对这4口斜井进行垂直深度校正，并以其中1口井（1井）的深度为标准深度，另外3口井（2井、3井、4井）的深度以此为标准作深度匹配。对比这4口井的声波测井曲线，选择出井眼状况稳定且泥岩特征明显的层段（图2）。图示层段为井段质量较好，声波测井曲线和井斜测井曲线较稳定的层段。

以这4口井的声波测井数据为基础，采用前面讨论的方法，编制地层真垂直深度（TVD）校正程序，最小二乘法反演校正程序，实现对所选层段汤姆森系数ε的确定。应用汤姆森系数ε、各井的倾斜角θ、声波测井速度VPH、VPV和自然伽马测井计算的泥质含量VSH，依据椭圆方程对这4口斜井的纵波速度进行各向异性校正，最终获得了泥岩的真正纵向速度。校正后的结果如图3所示。从泥质指示曲线（自然伽马GR和泥质体积VSH）可以看出此层段的顶部、中部和底部泥质含量较高；此层段的井斜角为32～34°之间；校正量普遍在15%左右。

图2 渤中区块4口井的声波和井斜对比图

图3 纵波速度的各向异性校正

对井斜角为80°左右的相同层位的随钻声波测井实施校正，选取的测井曲线的深度为斜深，校正结果如图4，可以看到在井斜角很大的情况下，校正量达到了20%～30%。由此可见在大斜度井中，由于泥岩各向异性和井斜的影响，实测速度与地层真正垂向速度的差异巨大。

3 结 论

1）以渤中区块的4口倾斜井为例，首先对这4口斜井进行垂直深度校正，并以其中一口井的深度为标准深度，另外3口井的深度以此为标准作深度匹配，找出对比标志层，以椭圆方程作为反演模型，采用最小二乘法确定汤姆森系数，实现泥岩速度各向异性校正。

2）渤中地区校正结果表明井斜角在不大于35°时，校正量不超过10%；当井斜角较大时，校正量可达到20%～30%。可见大斜度井中实测声波速度与地层真正垂向速度的差异巨大，斜井测井刻度地震实际应用中必须进行校正。所提出的方法克服了泥岩实验的困难和地震反演求取汤姆森系数的繁琐，为斜井泥岩速度各向异性校正提供了一种简明有效的新方法。

［1］Passey Q R，Yin H，Rendeiro C M ，et al.Overview of high－angle and horizontal well formation evaluation：issues，learnings，and future directions［J］.SPWLA 46th Annual Logging Symposium，2005，June 26～29.

［2］Hornby B E，Howiez J M，Ince D W.Anisotropy correction for deviated－well sonic logs：Application to seismic well tie［J］.Geophysics，2003，68（2）：464～471.

［3］Tien－when Lo，Coyner K S，Toksijz M N.Experimental determination of elastic anisotropy of Berea sandstone，Chicopee shale，and Chelmsford granite［J］.Geophysics，1986，51（1）：164～171.

［4］付强，罗彩明.基于VTI介质理论的P波速度分析和动校正［J］.物探化探计算技术，2008，（1）：10～16.

［5］卢明辉，唐建侯，胡彬，等.VTI介质P波非双曲时差分析［J］.地球物理学进展，2005，20（2）：328～331.

［6］邓继新，史哥，刘瑞珣，等.泥岩、页岩声速各向异性及其影响因素分析［J］.地球物理学报，2004，47（5）：862～868.

［7］Wang Zhijing.Seismic anisotropy in sedimentary rocks，part 1：A single～plug laboratory method［J］.Geophysics，2002，67（5）：1415～1422.

［8］Wang Zhijing.Seismic anisotropy in sedimentary rocks，part 2：Laboratory data［J］.Geophysics，2002，67（5）：1423～1440.

［9］Leon Thomsen.Weak elastic anisotropy［J］.Geophysics，1986，51（10）：1954～1966.

［10］Hornby B E，Schwartz L M，Hudson J A.Anisotropic effective－medium modeling of the elastic properties of shales［J］.Geophysics，1994，59（10）：1570～1583.

New Methods of Shale Acoustic Velocity Anisotropy Correction in Deviated Wells

QIAO Yue－dong（CNOOC Research Institute，Beijing100027，China）
SUN Jian－meng，GENG Zun－bo（College of Georesources and Information，China University of Petroleum，Dongying257061，Shandong，China）

The acoustic wave measured in deviated wells recorded the anisotropy of compressional wave in shale.It was necessary to determine the Thomson Coefficient in anisotropic correction，traditionally shale testing or seismic data were used to obtain the Thomson Coefficient by using inversion of VTI media dual curves.In allusion to the problem existed in the 2methods，it was proposed that on the bases of data comparison between many deviated wells，the logging acoustic data of multiple wells in a same horizon were chosen for obtaining the Thomson Coefficient by using an elliptic equation as inversion model and least square method，by which the anisotropic correction was implemented.The application in Bozhong Area indicates that the measured data is much different with of those in actual formation，the correction is as much as 20%～30%，by which accurate acoustic velocity is provided for a seism and inversion in deviated wells and accuracy is improved for the application of deviated well logging calibration.

deviated well；shale acoustic velocity in logging；anisotropy；correction；Thomson Coefficient

P631.84

A

1000－9752（2010）05－0104－05

2010－08－16

国家科技重大专项（2008ZX05023－005）。

乔悦东（1966－），女，1988年江汉石油学院毕业，高级工程师，现从事测井岩石物理研究工作。

［编辑］ 龚 丹