气井井筒积液模型与目前预测解法回顾
2010-11-15编译彭旭西安石油大学石油工程学院
编译:彭旭 (西安石油大学石油工程学院)
刘继梓 (长庆油田第六采油厂采油工艺研究所)
周凯 (延长油田股份有限公司勘探部)
审校:陈姣妮 (西安石油大学石油工程学院)
气井井筒积液模型与目前预测解法回顾
编译:彭旭 (西安石油大学石油工程学院)
刘继梓 (长庆油田第六采油厂采油工艺研究所)
周凯 (延长油田股份有限公司勘探部)
审校:陈姣妮 (西安石油大学石油工程学院)
气井井筒积液过程是多相流过程,井筒中流体产生回压 (通常重力压强起主导作用),该回压会限制,特定条件下甚至会阻止储层中气的产出。工业上已认识到井筒积液的重要性,并积极采取措施避免这类问题,然而对多相流间相互过渡现象却认识不足。本文讨论多相流复杂性与气井井筒积液间关系。综合回顾预测井筒积液产生的流动模型方程,诊断井筒积液对气井产量的影响,并进行最优化筛选。回顾了储层和井筒动态交互作用的最新模拟试验,指出当前模型存在的缺陷,并提出多相流型转变方法的重要性。
气井井筒积液 多相流 流型临界气流速度
1 引言
存在井筒积液的气井不能自行清除伴随采出气而产生的积液。产生井筒积液现象的前提是向上的气体流速远低于临界流速值,该值指最初被吸进气流的液体开始发生回落时的流速值。液体在井底不断积聚,增大储层静水压头,使井筒多相流不稳定(流型发生变化),且降低生产速度,严重时甚至导致死井。
典型井筒积液过程如图1所示,图中:
(1)生产初期,气体有足够流动能量将全部液体带出井筒,井筒中无液体回落;
(2)气井生产一段时间后,气流速度降低或含水量升高,导致气井没有足够能量将所有液体带上地面,造成液体开始回落;
(3)产生积液;
(4)随着井底静水压头增大,积液量不断增加,达到一定程度后积液重新侵入近井区域的储层;
(5)积液侵入储层后,气井又变成“无载的”,井筒气体又能再次流动,且气体能将井筒中所有液体带到地面。
从 (1)到 (5)不断循环,也是对气井井筒积液的典型间歇反应,直到储层潜力开始下降或产液量上升,这种循环才被打破。

图1 井筒积液机理 (Veeken等,2003)
井筒存在液相有以下三方面原因:
◇水蒸汽在井筒中冷凝;
◇从井底到地面随着压力及温度的降低,水蒸汽冷凝后在井底或储层近井区域沉降 (冷凝水饱和度在临界值之上);
◇地层水吸出会导致储层压力下降。
井筒积液常发生在低能量储层及致密气层,具有高气液比的高产储层也会产生井筒积液。因受污染井在没受到显著伤害的很长一段时间内可继续生产,所以井筒积液通常较难判别。井筒积液典型特征包括累计产量递减曲线有大的落差;近地面井筒开始出现段塞流;流压梯度突然变化;井口温度降低;产水量或冷凝水气比降低等。
图2为气井动态数据与时间关系曲线图,从图中可看到井筒积液产生。
尽管已使用大量技术减轻井筒积液影响,但若要针对特定积液进行最优方案选择,石油天然气工业仍缺乏可靠预测模型 (Lea等,2003)。
目前,用以预测和判别井筒积液的模型基本一成不变,因此不能用来处理典型井筒积液过渡现象,如在井筒中逐渐形成静液柱,及对地层伴生的回压。即使使用井筒多相流过渡模型,井底流入动态关系问题仍未能校正。

图2 气井动态数据显示井筒积液 (Sutton等,2003)
在井筒多相流过渡模型中将用到更可靠的方法,包括以储层近井区域过渡特征为边界条件的方法。该综合动态模拟方法研究积液上载/下载过程(图1),包括积液重新转入储层的可能性 (图3)。

2 目前模拟方法
通过理解与井筒积液相关的多相流,尽量避免积液产生。虽然预测流动条件的主要成果已形成,无井筒积液的区域仍使用所谓“Turner标准”,但这些都没能得到积液后动态。Turner标准被用来设计气井生产系统,即充分利用气体能量把井筒积液举升至井口,但是不能解释积液发生的严重程度及减产速度。
2.1 井筒积液预测模型
Turner等人 (1969)应用“微滴模型”,该模型通过流动微粒运动推算临界气流速度,用流速的力举升直井液体微粒。该模型最小流速需要保持液滴处于悬浮状态,这需要有两个力保持平衡,①气流向上的拉力 FD;②液滴自身重力 FG。方程如下:
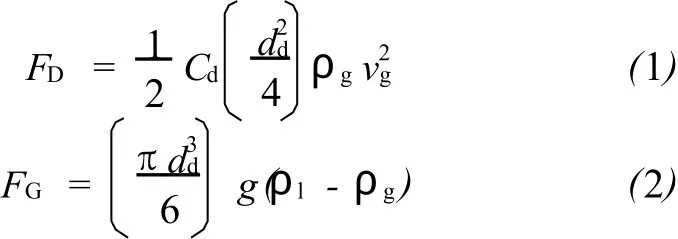
气体-微滴系统及作用在微滴上的力可用图4描述。
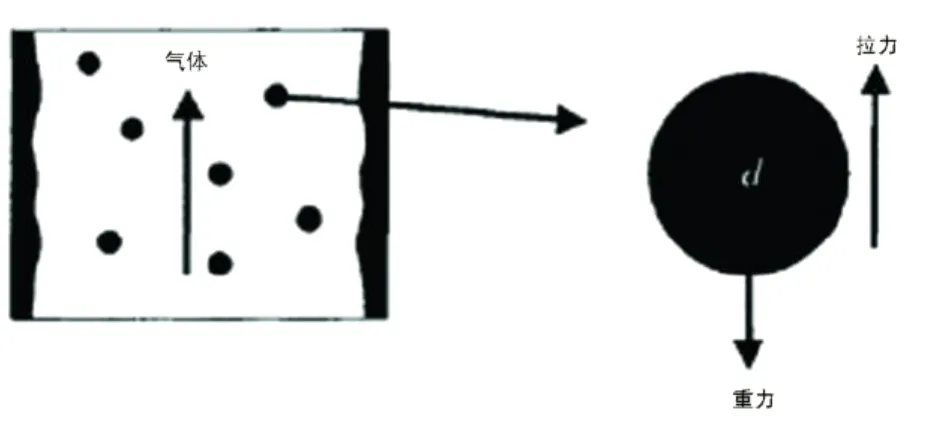
图4 液滴在垂向气流中的运移 (Lea等,2003)
给定井筒沉降条件,FD比 FG大时,气体流速比临界流速大,这样可把液滴举升起来,且液滴充满井筒环状空间 (井壁上存在一层流动着的液膜,气体携液滴在管柱中心流动),相反若 FD小于FG,流型将变成涡流或段塞流,致使液体回落到井底——形成井筒积液。当 FD=FG时可求得临界气流速度,即:

求解式 (3),得气流速度:
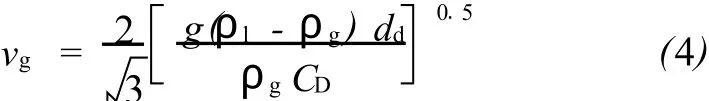
液滴直径 dd随气流速度而变化,可表示为韦伯数的函数 NWE:

从式 (5)、(6)可知,液滴间作用力越大 (相对较高气体流速),微滴体积越小。将式 (6)代入式(4)得:

Turner等人 (1969)指出查表能得到具有足够精度的表面张力,形态及雷诺数对牵引系数影响较大。对典型现场条件,雷诺数范围为104~2×105。该雷诺数范围内,球状微滴的牵引系数约为0.44。1955年 Hinze提出韦伯数范围 (20~30),选其最大值,1969年 Turner等人为得到临界气流速度,引入以下方程式:为配合井口压力大于或等于800 psia(1 psi=6.895 kPa)的气田现场数据,式 (8)需进行20%的调整。

1991年 Coleman等使用 Turner的“液滴模型”(1969年)测定井口压力在500 psia或更低时的临界气流速度,发现实例中不需作20%的调整。还注意到气体重力、界面张力及温度对气体的临界流速计算有细微影响,而占主导地位的影响因素是井径与井口压力。观察到气井出现段塞流时,并不服从吸入微滴模型。
Nossier等1997年通过计算与现场数据相应的雷诺数,检验 Turner等的湍流假设。发现几乎所有初期采用的现场数据都超过导出式 (8)的雷诺数假定范围 (104~2×105),雷诺数范围应为2×105~106,对应牵引系数为0.2,因此为配合现场数据需进行20%的调整。由Coleman等人提供的据现场数据计算的雷诺数最初假设范围为 (104~2×105),因此几乎不需要调整即可与现场数据匹配。此后Nossier等推导出两种吸入微滴模型:低流速模型和高流速模型。
对于低流速模型,计算临界流速的公式如下:

把式 (6)代入式 (10),得:
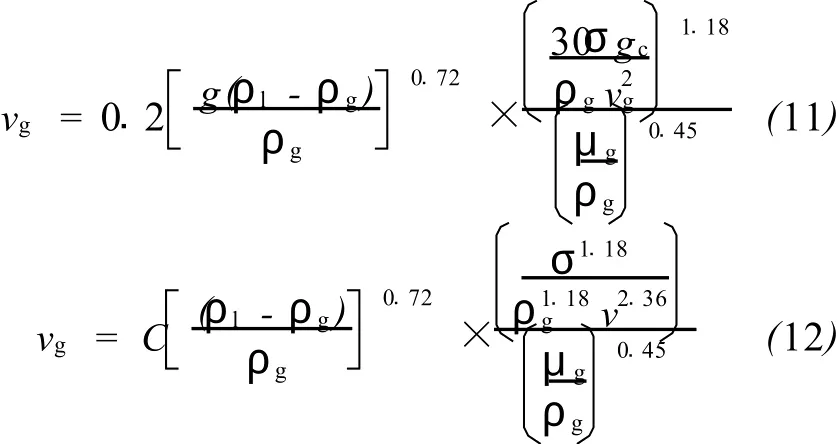
式中 C =8094.5=0.2×32.170.72×301.18×32.171.18,由此整理上式得:

对于高流速模型,将 (6)式 (假设韦伯数为30)代入 (4)式,得临界流速公式:
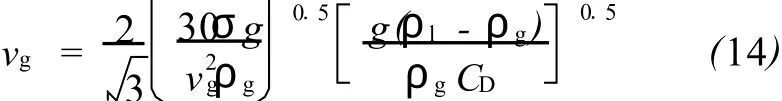
令CD=0.2,得:
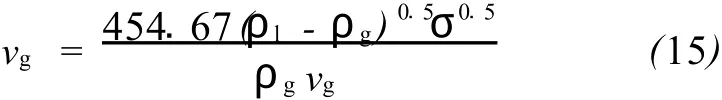
最终解得vg:

吸入微滴模型广泛用于油气工业预测气井最低产气量并避免井筒积液产生。基于该法的模型已在不同程度上成功地检验了现场数据。
预测临界流速的精度取决于井底流动压力梯度。但这也会出现一个新问题:与压力梯度相关的预测条件显示一种流型,但是临界流速的计算结果又显示另外一种流型。
超出微滴模型适用范围的较高压力对参数作用后仍可用作实验数据,因此可确定预测临界流速的精度界限。
当井筒积液时,预测临界流速及井筒积液的方法并不模拟井筒中流入状态。该法仅提供估计液体回落时气流速度值的标准。
2.2 典型井筒积液的井筒多相流过渡模型
为模拟多相流与气井井筒积液的关系,辨别井筒中流体相态并从流动力学角度描述该现象是很有必要的。
关于多相流的相态,气井积液问题通常被认为是气-液两相流问题。然而对液相来说,里面可能含地层水、冷凝水及天然气凝析液。由于积液组成不同,其物理性质和与气相相互作用时可能不同。
为从流动力学角度来对井筒积液进行描述,需充分理解流动型态和流动型态的转变。多相混合物相与相界面间的形状和特性规定其“流动型态”或“流型”。同时多相流内部存在竞争力或竞争机理。两者间的平衡决定流型。
对气液两相流而言,控制界面分布的因素相当复杂。因素包括界面张力、润湿性、扩散性、凝聚性、主应力和热流影响。尽管流体的详细特性仍取决于相对重要的影响因素,但在某确定大类中 (流型)区分出界面分布类型还是可能的。虽然对流型分类的出发点很好,但其系统本身并不完全符合技术要求。应强调相对重要的影响因素随着相流速变化而变化,且流型转变的界限并不是非常明显。这导致人们判别流型时更多依靠主观划分。
为描述气井井筒积液,有必要预测从合格流型(环流或者雾流)变为不合格流型 (涡流)的转折点,涡流的出现意味积液的开始。井筒积液产生过程对应非稳定流流动状态。假设气井井筒内初始状态是稳定的环流,流型第一次转变是由产气量下降引起的 (或由于产水量上升)。流型由环流变成涡流,这时可认为开始积液。紧接着涡流转变为段塞流。井底增加的积液加大对储层的回压,同时阻止天然气流入,图5显示不存在积液时气井的流型变化 (从泡流到环流)。

图5 (0)泡流 (1)段塞流 (1-2)涡流 (2)环流
就经验模型而言,经验方程中摩擦压力梯度数据及真实含气率始终与系统参数有关。为了完善经验模型,需大量实验来重现这个特殊问题,但也许代价昂贵,即使因次分析能实现,这样的计算模型也仅仅在一定条件下适用。总的来说,经验模型虽缺乏基本物理解释,但其主要优势为公式简单且计算快速。
1974年 Gray将经验模型用于高天然气组分气液两相流研究。对垂直管流,计算井筒中参数:所携液体的温度梯度、流体加速度以及天然气组分中的非烃化合物,并由以上参数计算两相压降。Kabir和 Hasan 2006年指出 Gray采用一种假均质流法计算由摩擦力、重力和加速度所引起的压力损失。考虑到液体微滴速度有可能达不到气流速度,微滴可能发生滞后,因此 Gray模型并非完全均匀模型。
在Gray的模型中没有区别流型,该模型也仅能应用于稳定流或伪稳定流,因此该模型并不适合典型井筒积液的过渡现象。
逻辑现象模型是在识别特殊流动类型与对特定压降计算的应用基础上发展起来的。闭合边界条件是必要的 (如对真实含气率的定义)。确定流型的关系需一同确定各流型之间转变点标准。起初流型根据两相流观察结果分类。实验观察结果为二维平面图 (流型图)和所鉴定流型的区分范围。过去,为在已建立实验中寻找独立参数,对二维平面图采用不同坐标形式 (如质量流量、动量流量或者表面速度)。然而,即使运用现代检测手段来发展流型识别技术,对所观测流型的判断仍相当主观。如2006年Falcone也讨论过逻辑现象模型在两相流中的应用例子。
至今,两相流模型和漂移模型已用于典型井筒积液的不稳定流基本方程计算。
两相流模型讨论流体 (气和液)时认为它们在井筒内是独立流动的。针对气、液、液滴的独立连续性方程已出现。使用两个动量方程:①气和吸入液滴的综合方程;②独立液体方程。目前一个混合物能量守恒方程已得到应用。可看出合理的定律是必要的 (通常来自经验数据)。1991年Bendiksen等、2006年Shoham都讨论和推导过气液两相流守恒条件。
漂流模型主要由 Zuber和 Findlay(1965),Wallis(1969)及Ishii(1977)建立起来。尽管气液两相间可能存在滑脱现象,该模型仍将两相看成混合物。目前普遍认为漂流模型较适合混合流,混合流指两组分间的动力学能接近耦合 (Ishii和Hibiki,2006)
关于两相流和漂移流动方法,有几点限制:
◇流动型态,如段塞流,其在自然状态下是间断的,并不符合两相流模型。在垂直向上的段塞流中,流体在井筒中向上流动,但向下却是泰勒气泡区,这使流体物性很难平均;
◇两相流法也并不能完全描述涡流,该流动型态可认为是一种特殊的环流,即环流的液膜经历周期性反向;以波浪状将液体向上传输;
第一,绝大多数人不可避免地失业。无论地球上的所有人多么努力,并且,无论每个人多么聪明,绝大多数人都会失业,因为岗位非常有限。众人皆聪明、努力,只会提高就业门槛,并不会增加就业机会。此点几乎是刚性的,也是最重要的,它使绝大多数人即便终生学习也无法改变命运。
◇在多数独立流动过程中,相与相间的相对流动与压力梯度、速度梯度直接相关,漂流模型不能描述这类情况;
◇无论两相模型还是漂流移动模型,均需要相关闭合边界条件来描述气液界面张力和井壁摩擦力。
2.3 井筒积液情况下描述储层和井筒间动力相互作用的模型
图6所示是一条典型IPR曲线,描述气井井底流入压力与典型油管动态关系 (TPR),TPR主要描述产气量特征。若根据上图方法测得产气速度,那么该产气速度即为特定系统的临界气流速度,结果可能产生井筒积液。

该方法忽视了井筒及储层近井区域间的过渡流,这种过渡流是气井井筒出现积液的象征。当描述积液间歇特征时,为把井筒及储层近井区域两种系统联系在一起,必须定义储层和井筒间接触面的实际过渡边界条件。
Sagen等2007年就储层近井区域提出一种隐式耦合解法,该法建立在有限差分模型基础上。这种方法模拟以多孔介质为接入点,流体进入过渡井筒模型的传输过程 (最初是Bendiksen等在1991年模拟的管流)。油藏模型输出结果是时间和空间上的压力和饱和度,而输入则为多孔介质的渗透率和孔隙度,以及液相的物性。井筒模型为油藏模型提供压力边界,而油藏模型模拟管流及流体温度。据Sagen等2007年研究成果可知,隐式连接法可用以下几句话概括:最初井筒模型给定一个时间步(n+1),通过油藏模型可计算流入敏感性参数 an和bn,有以下关系:

Pp——井筒模型压力;
MP——每一相的质量流量,下标p代表给定
可用 (17)式作为井筒模型边界条件。井筒模型完成(n+1)个时间步迭代,并把 Pn+1p和Mn+1P传回到油藏模型,而油藏模型又使用由井筒模型提供的边界条件,完成(n+1)个时间步迭代。储层中流入敏感性参数an和bn由前一个时间步n计算得出,流入参数表达式如下:

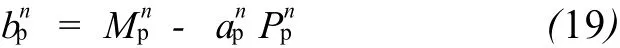
所提议耦合模型 (稳态油藏模型和过渡井筒模型)的目的是尝试通过单管模型解释储层和井筒间的相互作用。
Dousi等2005年引进一种分析方法,即采用稳态计算模拟储层流入动态和井筒流出动态,以此研究气井井筒积液。该方法在假设气井生产过程中出现两种流型:①气液同产的流型;②亚稳定流型,当较重的相被重新注入储层时便会出现这种流型。图7描述气井井筒积液过程。
图7中的模拟过程分析如下:
◇起初气井以定产量生产,此时有足够能量将液相完全举升到地面;
◇随着井口回压增加或地层压力下降,气井流速降低到临界 Turner值以下,导致产出水开始向井底回流。随着井底积液量增加,对储层产生一个较高静水头压力,导致储层生产压差减小,最终减少气液产量;
◇稳定条件下,显示气井水淹前状态;
◇液体生产速度等于液体回注速度时的情况。
尽管该解析法仍需流体力学方面的验证,但该方法代表了井筒积液时回注到储层液相的量化尝试。

图7 因重相回注而产生井筒积液的模拟过程
3 结论
对于实际生产中气井井筒积液的认识仍很匮乏,尤其是储层和井筒之间的动态关系。
描述了井筒积液的复杂性、预测井筒积液的技术方法,同时也模拟了各阶段的流型。对最新储层和井筒间相互关系的模拟也进行了描述。
临界气流速度的估计建立在稳定流假设条件基础上,因此,不能描述与积液有关的流型变化的复杂性。
尽管大量两相流模拟技术已得到应用,但描述流型转变时仍有困难,如:从环流到涡流,从涡流到段塞流,最终段塞流变成泡流,这会导致气井死井。
即使气井过渡模拟技术已被采用,但用以联系气井动态与储层间歇反应的预测模型是不可靠的。这意味着错误定义了两个子系统的边界条件,也意味着关于液相重新注入储层的问题仍需得到流体力学证明。
最近,模拟储层与气井间动态关系的尝试还需进一步努力和验证。一个专门的流动循环被用来模拟非稳态流条件下近井区域的动态交互作用、多孔介质与井底之间的动态交互作用。
在油气生产过程中,需要可靠的预测模型,这样才能针对井筒积液选择最佳的解决方案。
10.3969/j.issn.1002-641X.2010.3.013
资料来源于美国《SPE 115933》
2009-03-28)
