基于粒子群算法的梯级电站日优化调度

郑体超, 李 永, 朱 明, 张 平

(1.四川省港航公司金银台航电枢纽,四川 阆中 637400;2.四川大学水力学与山区河流开发保护国家重点实验室,四川 成都 610065)

梯级电站日优化调度是在考虑梯级水库水位、电厂出力、下泄流量、电网需求、峰谷电价差等约束的前提下,以次日梯级上游水情为边界条件,以日发电量最大为目标,优化次日梯级电站总发电量与出力过程,优化结果可作为梯级电站竞价上网与调度决策的参考[1]。

1 梯级电站日优化调度模型

1.1 目标函数

以梯级电站发电量最大为优化准则,所构建的梯级电站日优化调度目标函数如下:

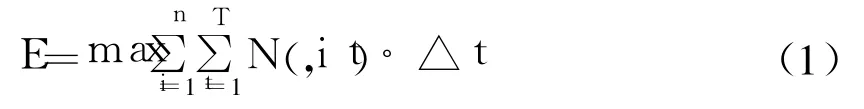
式 1中,E为调度期梯级总发电量最大目标函数;n为梯级电站数,i表示第 i梯级电站,i=1,2,…,n;T为日调度时段数,t表示第 t调度时段,t=1,2,…,T;N(i,t)为第 i梯级电站 t时段平均出力;Δt为调度时段长。

1.2 约束条件

(1)水量平衡约束:

V(i,t+1)=V(i,t)+(Qr(i,t)-Q(i,t)).△t (2)

Q(i,t)=Qf(i,t)Qs(i,t) (3)

Qr(i,t)=Q(i-1,t-τi)+Qu(i,t))(4)

式 2、3、4中,Q(i,t)为第 i梯级第 t时段平均出库流量;Qr(i,t)、Qu(i,t)、Qf(i,t)和 Qs(i,t)分别为第 i梯级第 t时段平均入库流量、区间入流、发电流量和弃水流量;τi为第 i梯级与第 i-1梯级之间的水流传播时间。

(2)下泄流量约束:

Qmin(i)≤Q(i,t)≤Qmax(i) (5)

式 5中,Qmin(i)为第 i梯级 t时段的最小下泄基流量;Qmax(i)表示第 i梯级的最大泄流能力。

(3)库容约束:

Vmin(i)≤V(i,t)≤Vmax(i) (6)

式 6中,V(i,t)为 i梯级 t时段期末的蓄水量;Vmin(i)和 Vmax(i)分别为第 i梯级的允许最大、最小蓄水限制。

(4)出力约束:

Nmin(i)≤N(i,t)≤Nmax(i) (7)

N(i,t)=A(i).Qf(i,t)◦h(i,t) (8)

式 7、8中,N(i,t)表示第 i梯级 t时段的平均出力;Nmin(i)为各梯级电站技术最小出力,Nmax(i)为各梯级电站的装机容量或机组预想出力;A(i)为第 i梯级电站出力系数;Qf(i,t)为第 i梯级t时段平均发电流量;h(i,t)为第 i梯级 t时段平均水头。

(5)非负约束:模型中的所有约束均为非负。

2 粒子群算法智能优化算法

粒子群算法(ParticleSwarmOptimization,PSO)[2]由美国社会心理学家 JamesKennedy和电气工程师 RussellEberhart博士于 1995年提出,是一种模拟群体智能行为的适合于复杂系统优化计算的自适应概率优化技术。在粒子群优化算法中,每个优化问题的可能解是 D维搜索空间上一个点,被称之为“粒子”。粒子群优化算法的优化搜索是在由随机初始化而形成的粒子种群中,以迭代的方式进行。粒子群优化算法的迭代公式如下[3]:

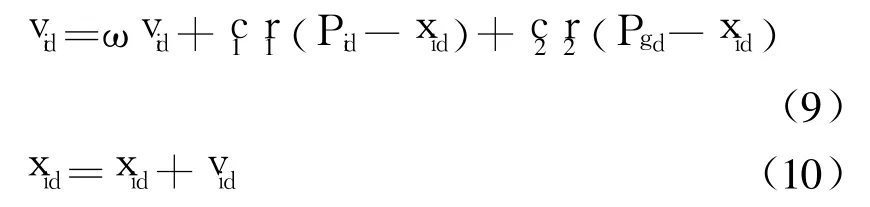
式 9、10中,i=1,2,…,m;d=1,2,…,D,D为空间维数;ω为惯性权重系数;c1、c2为学习因子;r1、r2为[0,1]区间上的随机数;vid为粒子搜索速度;xid为粒子搜索位置;Pid为粒子自己最好的位置;Pgd为群体最好位置。

在式 9、10中,粒子利用以下信息改变其位置[2]:(1)当前位置;(2)当前速度;(3)当前位置与自己最好位置的距离;(4)当前位置与群体最好位置的距离。

粒子群算法具有搜寻效率高、流程简洁、易于收敛等特点,近年来发展很快,已在许多方面得到成功的应用[4]。粒子群算法也适合于求解高维、非线性的梯级电站日优化调度问题[5]。

3 应用分析

选择嘉陵江中游金银台、新政与金溪梯级航电枢纽(以下简称“金银台三梯级”)历史调度资料中的某典型调度日,以验证粒子群算法求解梯级电站日优化调度模型的有效性。

3.1 嘉陵江中游金银台、新政与金溪梯级概况

嘉陵江系长江支流,发源于陕西省凤县秦岭南麓黄牛铺,流经甘肃、四川,至重庆市注入长江。全流域面积 159812km2,年径流量 670亿 m3,干流河道全长 1119km,广元以上为上游,广元至合川为中游,合川至重庆为下游。干流中游是嘉陵江梯级开发的主要河段,其中亭子口水库是控制性枢纽。

在嘉陵江中游,已建成并运行较长时间的航电梯级枢纽为金银台、新政与金溪航电梯级,由于金银台、新政与金溪航电梯级同属一家发电企业,而且金银台在日调度中的来水情况由上游白龙江支流控制性枢纽宝珠寺、干流亭子口水文站以及支流东河清泉乡水文站提供,具有较好的预见性。因此,如将三个梯级进行联合调度,可能挖掘的发电效益将较为可观。金银台三梯级的基本参数如表 1所示。

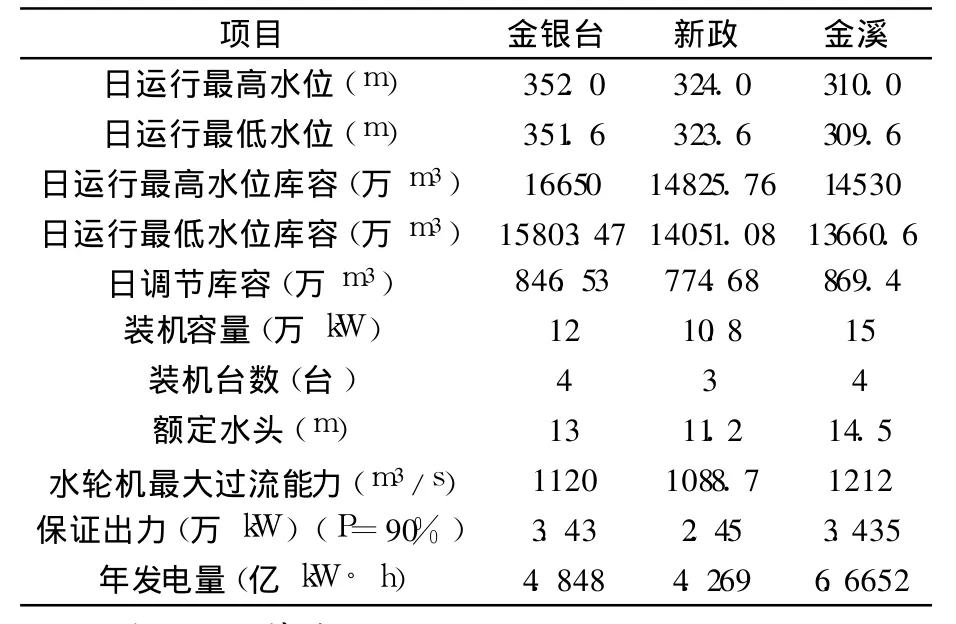
表 1 金银台三梯级基本参数

3.2 粒子群算法流程

采用粒子群算法求解基于梯级电站短期优化调度问题时,决策变量可选择为各梯级下泄流量,状态变量可选择为各梯级库区水位,求解算法流程可设计如图 4-1所示。

3.3 模型参数设置

针对求解梯级系统短期优化调度模型的粒子群求解算法参数设置如表 2所示。

表 2 粒子群算法参数

3.4 约束处理

在模型求解过程中,对约束条件的处理主要采用以下三种方法[6]、[7]、[8]:

(1)限制搜寻范围。在模型求解过程中,限制粒子在约束条件要求的范围内搜索。

(2)保留可行解。在粒子寻优过程中,保留可行解,淘汰非可行解。

(3)罚函数法。罚函数法的基本思路是将约束优化问题转换为无约束问题求解。罚函数是将目标函数和约束进行某种组合后得到的函数。如原目标函数为 Fd,则经罚函数法处理后新目标函数 F为:F=Fd+βi◦ ET

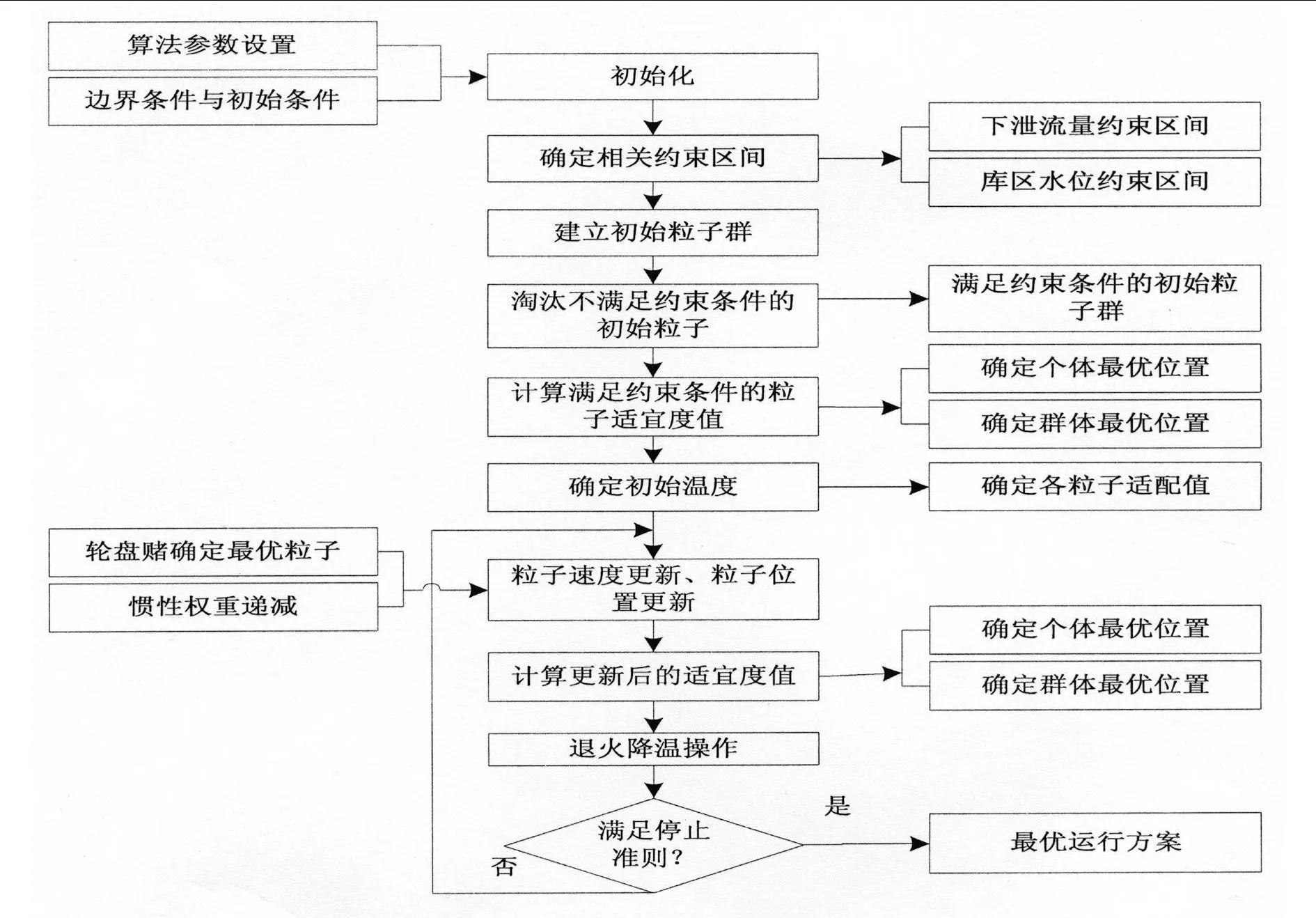
图 1 粒子群算法流程

式中,ET为越限向量,ET=(e1,e2,…,ek),ek为第 k个约束的越限量;βi=β1,β2,…,βK为惩罚系数向量,βk为第 k个约束的惩罚系数。

3.5 模拟优化调度结果及对比分析

模拟优化典型调度日的选择为:2009年 12月 8日 00∶00～24∶00。在该典型调度日,金银台枢纽的入库流量过程如图 1所示。

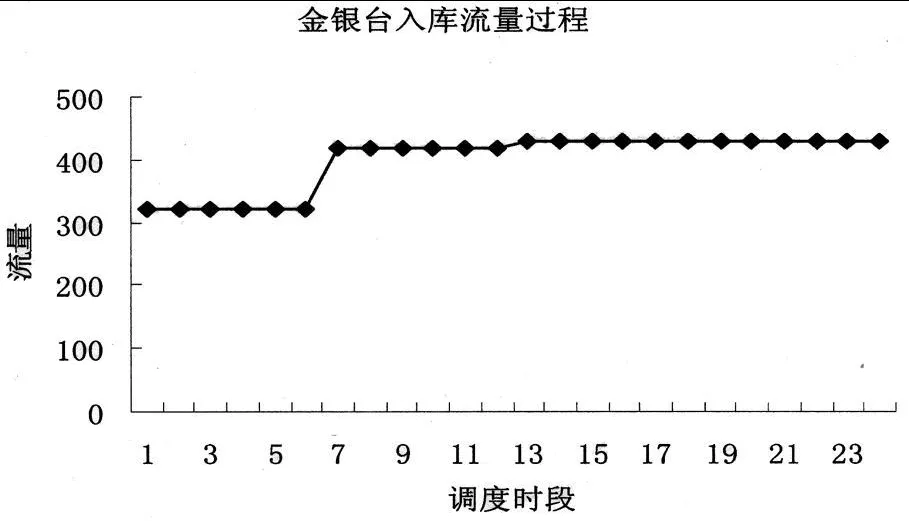
图 2 金银台入库流量过程

采用相同的边界与初始条件,对金银台三梯级的日优化调度模型进行编程求解,可得到金银台三梯级在典型调度日的模拟优化调度方案。

典型调度日模拟优化调度的梯级总发电量与实际发电量的对比如表 2所示。

典型调度日模拟优化调度的梯级总出力过程如图 2所示,梯级的实际总出力过程如图 3所示。

在典型调度日模拟优化调度过程中,各梯级水位过程如图 4～6所示。现对典型调度日的模拟优化调度结果与实际调度结果进行对比分析如下:

表 3 典型日模拟优化调度的梯级总发电量与实际发电量对比

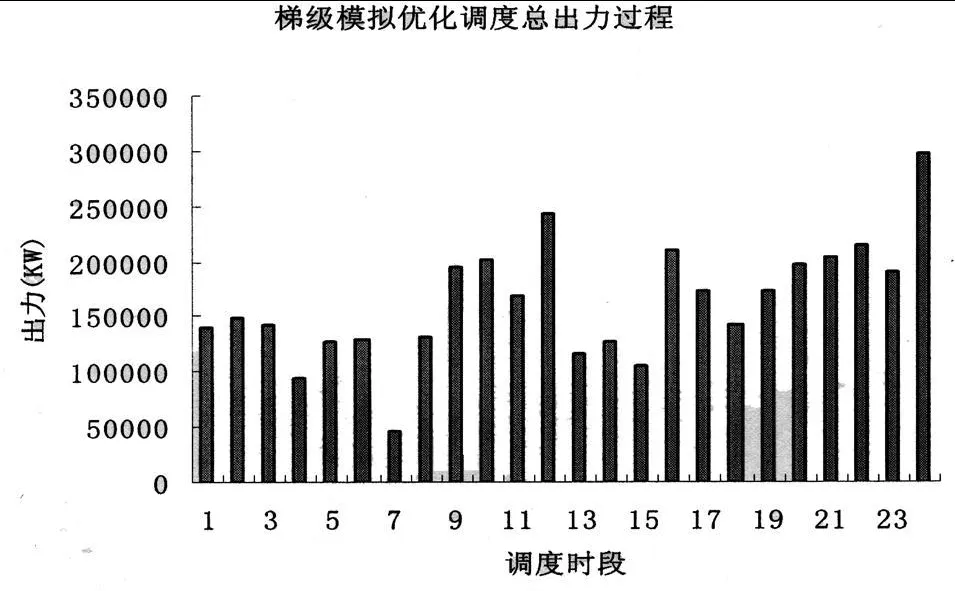
图 3 梯级模拟优化调度总出力过程

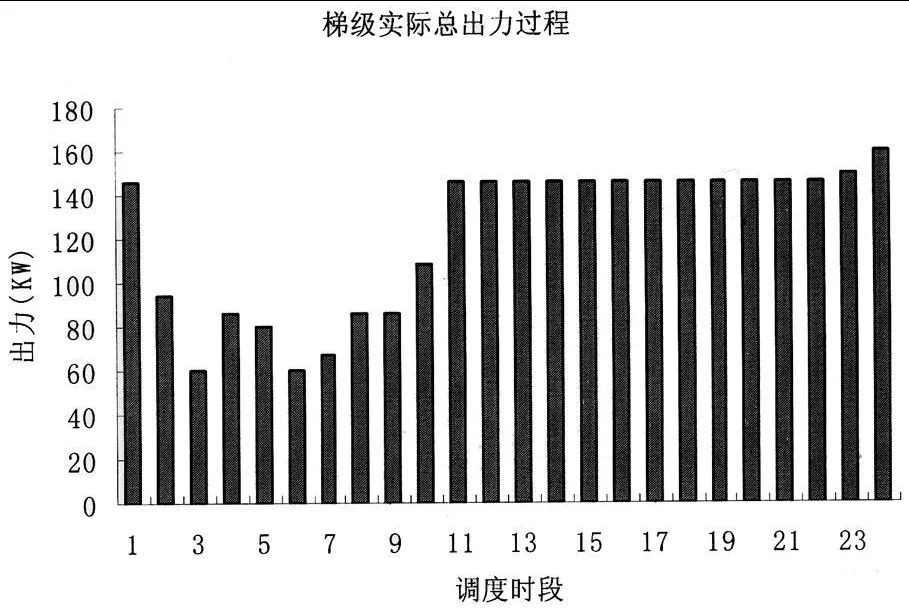
图 4 梯级实际总出力过程

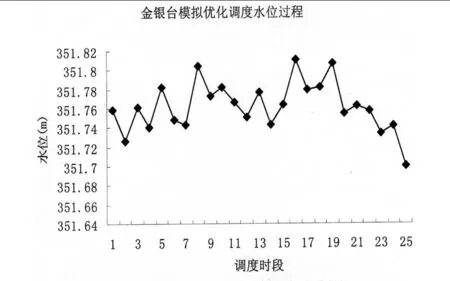
图 5 金银台模拟优化调度水位过程

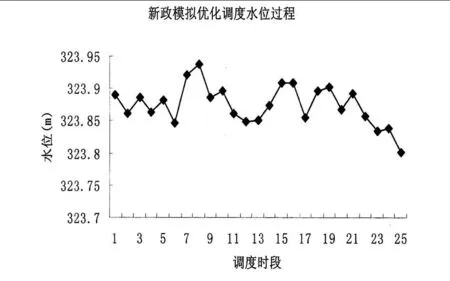
图 6 新政模拟优化调度水位过程

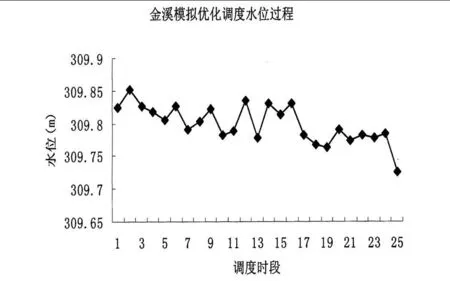
图 7 金溪模拟优化调度水位过程

(1)由表 3可知,模拟优化梯级总发电量为3948069kW◦h,梯级实际总发电量为 3533736 kW◦h,由优化所增加的发电量为 414333kW◦h,增加幅度为 11.7%。

(2)由图 3、图 4的对比可知,在模拟优化调度过程中,梯级在早高峰与晚高峰的总出力都高于其它调度时段较多,而在实际调度过程中,早高峰时,梯级总出力较低,而在晚高峰期间,梯级总出力也未明显高于其它调度时段。这表明模拟优化调度的结果更符合市场需求。

以上分析表明,采用粒子群智能优化算法所求解得到的嘉陵江中游金银台三梯级的模拟优化结果是较合理有效的。

4 结 语

采用粒子群智能优化算法,可避免多梯级水电站系统优化模型所产生的“维数灾”,能实现对梯级电站日优化调度模型的有效求解,从而得到梯级电站日优化调度方案,该方案可作为梯级电站联合竞价上网的参考依据,也可作为水库调度运行方式的参考,有助于梯级电站实现整体的发电效益最大化。梯级电站日优化调度模型的粒子群智能求解方法具有一定的应用参考价值。

[1] 周晓阳,张勇传,马寅午.水库系统的辨识型优化调度方法[J].水力发电学报,2000,(2):74-86.;

[2] KennedyJ,EberhartRC.ParticleSwarmOptimization[A].IEEEInternationalConf.onNeuralNetworks[C].Perth,Australia:IEEE,1995:1942-1948;

[3] 谢晓锋,张文俊,杨之廉.微粒群算法综述[J].控制与决策,2003,18(2):129-134;

[4] 杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2004,6(5):87-94;

[5] VandenBerghF.Ananalysisofparticleswarmoptimizers[D].SouthAfrica:DepartmentofComputerScience,UniversityofPretoria,2002;

[6] DebK.Anefficientconstrainthandlingmethodforgeneticalgorithms.ComputerMethodsinAppliedMechanicsandEngineering,2000,186(2):311-338;

[7] JoinesJ,HouckC.Ontheuseofnon-stationarypenaltyfunctionstosolvenonlinearconstrainedoptimizationproblemswith Gas.Proc.ofthe1stConferenceonEvolutionaryComputation.IEEE,1994.579-584;

[8] RichardY,FungK,TANGJF.Extensionofahybridgenetic algorithmfornonlinearprogrammingproblemswithequalityandinequalityconstraints.Computers＆OperationsResearch,2002,29:261-274.