舰船总布置中的综合评估模型及其应用研究

2010-11-12王健陈立

中国舰船研究 2010年1期

王健陈立

中国舰船研究设计中心，湖北武汉 430064

1 引言

舰船的总布置设计［1］是一个非常复杂的系统工程，战舰与民用船舶相比，需要配设大量雷达天线、武器装备、弹库和工作舱室等，并提供足够的生活、娱乐空间以满足舰上军官、士兵需求，因此，战舰通常面临在有限的空间资源下，对主要工作和生活舱室、通道、上层建筑主要电子武器装备的合理分布与布置进行综合研究，以保障总体布置的合理性，便于指挥、作战和人员、物质的通行，最大限度地减少相互间的妨碍和干扰，提高舰船的综合作战能力。

2 问题描述与数学模型

本文采用多目标［2-4］综合评估方法建立舰船总布置设计多目标决策模型。

设有多目标决策问题：

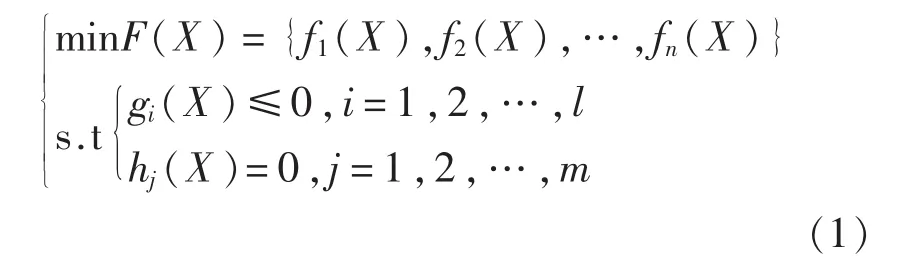
式中，X=（x1，x2，… ，xk）T为k维决策的向量；F为目标函数；gi（X）≤0和 hj（X）=0为系统约束［5］。

集合 S＝｛X＝Rk｜gi（X）≤0，hj（X）＝0，i＝1，2，…，l，j＝1，2，…，m｝称为可行集。

舰船舱室优化布置是一个典型的多目标优化问题，如果把n个目标函数集成在一起形成一个实值偏好函数，则可在相同的约束条件下，最优化偏好函数。这个模型称为“妥协模型”，而其解称为“妥协解”。常见的妥协模型是通过对目标函数进行加权而建立起来的。本文采用加权和法进行多目标决策，将多目标决策问题转化为单目标问题求解。

可将式（1）转化为如下对应的加权单目标问题：

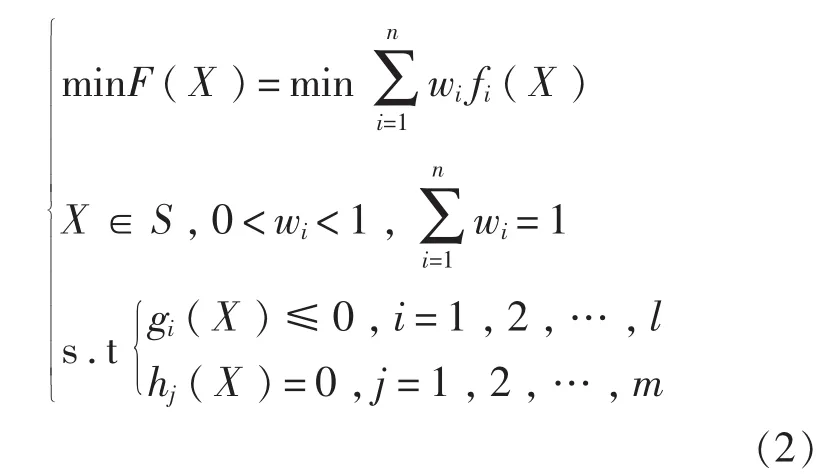
式中，wi为加权系数，wi的大小表明了第i个目标函数的重要程度。同时，目标函数 fi（X）（i＝1，2，…，n）应变换为无因次量。式（2）中 F（X）在舱室布置设计中可称为“多目标决策函数”，设计变量为舱室的空间参数X，这样舱室的空间参数即包括位置参数，即

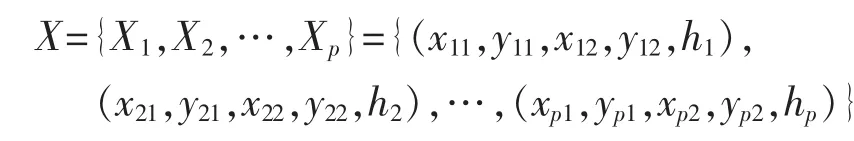
式中，p 为舱室总数量，（xi1，yi1，xi2，yi2，hi），i＝1，2，…，p分别为舱室i的左下角x坐标、左下角y坐标、右上角x坐标、右上角y坐标和舱室i的最小高度。

此外，为了满足舱室布置优化多目标评估模型的建立，还应将舱室进行类别划分。一般来说可按功能进行分类，可分为通道、有人员停留的工作舱室、住舱、设备舱室等。可通过建立舱室类别类参数CL方便判断舱室所属类型。

CL＝｛第1个舱室所属类别，2个舱室所属类别，…，第p个舱室所属类别｝

舰船总布置设计过程中，不仅要求最终优化方案满足给定的目标函数，同时要求符合一定的约束条件。这些约束来源是多方面的，针对不同的具体情况，舱室布置存在不相同的、隐性的约束方程。总布置优化中，普通存在的、也是最主要的约束类型为：

1）规范约束条件

它表达了舱室布置设计时应该遵循的布置准则、规范等；然而，将舱室布置准则、相关规范用约束函数形式表达存在相当的难度。本文假定已设计完成的多方案已充分考虑到规范、准则的约束。

2）几何约束条件

它反映舰船布置评估区域内舱室之间的空间位置约束关系。几何约束条件可以转化为等式约束和不等式约束。

等式约束主要是舰船设计空间和该区域内舱室间空间位置约束关系，如舰船各层甲板内舱室的约束关系可简化为面积为恒定值，可以用下式来表示。

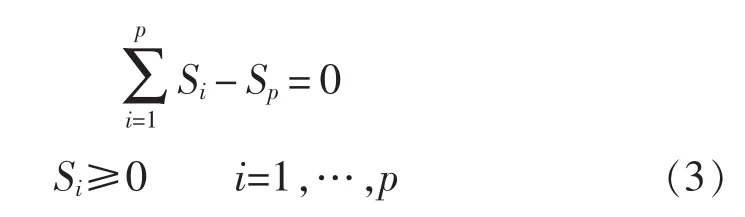
式中，p表示舰船布置设计所有舱室的总数；Sp表示该空间甲板总面积；Si表示第i舱室的面积。

不等式约束主要来自各舱室的不干涉条件，即两个舱室不能同时占用相同的空间。对于舰船内所有舱室，不干涉约束条件可表示为：

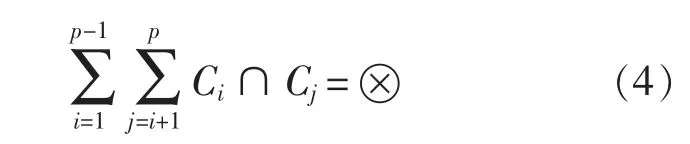
式中，Ci、Cj表示参考舱室；p表示舱室总数量。

每个单目标函数对多目标模型都有重要影响，针对舰船总布置设计，建立全面的、合格的目标函数应综合考虑该区段的功能需求、舱室类型，有人员停留舱室对舒适性的要求以及设备舱室、工作舱室的重要性等。一般有以下几种目标函数：

1）通道输送的连续性及畅通性函数f1（X）

通道直接影响战时与和平时期人员战位的进度、海补时的便利以及人员疏散的畅通。为准确地表达前后段通道对人员战位、输送连续性等带来的影响，目标函数f1（X）反应了通道对设计需求的满足程度，可定义为：

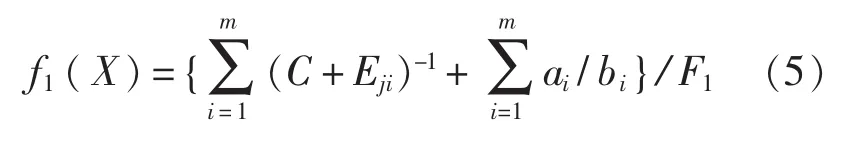
式中，m表示总布置设计的通道数；C为平衡系数，用来调节能量函数Eji对f1（X）影响的大小；ai表示第i通道的宽度；bi表示第i通道的长度。为避免各个目标函数差别过大情况，需要对每个目标函数标准化处理，F1可定义为目标函数f1（X）的基准值。能量函数Eji根据弹簧的势能原理得出，定义如下：

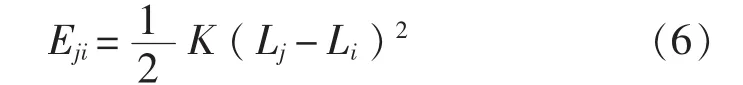
式中，K是弹性系数，可根据通道的重要性设定；L是通道i横向距船中心线距离；L是通道i向前相连通道j的横向距船中心线距离。接近关系意味着通道的设计需考虑到通道的纵向连续性，即通道间的纵向不连续则造成某种意思上的 “能量损失”。

2）有人员停留舱室的舒适度目标函数f2（X）

充分考虑到工作舱室、居住舱室的舒适性，可定义f2（X）表示有人员停留舱室舒适度评估的目标函数。

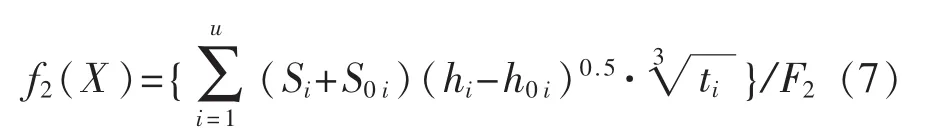
式中，u表示有人员停留舱室总数；ti表示第i个舱室人员停留的平均时间；S0i表示第i舱室基准面积，该值可取满足设计需要的最小面积；Si表示第i舱室当前方案的面积；h0i表示第i舱室基准高度，该值可设为满足布置需要求的最小高度；F2为目标函数f2（X）的基准值。

3）设备舱室布置目标函数f3（X）

定义f3（X）表示设备舱室进行目标函数布置的影响。

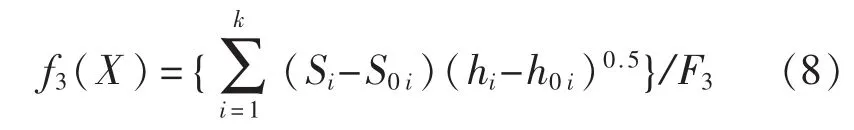
式中，k表示设备舱室总数，应注意随局部布置方案的不同，k值是变化的，在满足各舱室空间需求同时，k越大越可缓解舰船存在面积紧张的问题；S0i表示第i设备舱室满足布置需求的最小面积；Si表示第i设备舱室当前方案面积；h0i表示满足第i设备舱室布置需求的最小高度；hi表示第i设备舱室当前方案高度；F3为目标函数f3（X）的基准值，可通过一个已设计的布置方案计算得出。

针对舰船总布置设计的具体情况，还可建立其它目标函数，最后将所有目标函数加权处理可得综合评估函数。

2 对蚁群算法进行适应性改进

蚁群算法是近年提出的一种新型的随机搜索模拟进化算法，由意大利学者M.Dorigo等人首先提出，并用该方法求解旅行商问题、指派问题、job－shop 调度问题［6，7］等，取得了一系列较好的实验结果。蚁群算法的优点在于：它是一种并行算法［8］，所有“蚂蚁”（即算法中的工作单元）独立行动，不存在监督机构或约束机制；它是一种协作算法，每一只“蚂蚁”选择路径时，都要借鉴其它“蚂蚁”的搜索经验，有残留信息的路径被选中的可能性要比没有残留信息的路径大得多；它是一种鲁棒算法［9］，因为只要对算法稍作修改，就可以运用于别的优化问题，如文献［10］将蚁群算法应用于船舶主尺度优化。

在现实多专家评估的过程中，不同的评估者首先采用各自主观上的偏好，即各自采用不同的加权系数wi针对各方案进行评估，而后所有评估者交流意见、讨论并最终选定最优方案，这个过程则与蚁群算法中并行作业、相互借鉴过程非常相似。本文采用蚁群算法中的评估单元来模似现实中的评估专家。

针对舰船总布置方案，采用不同的加权系数wi（i＝1，2，…，n）则有不同的综合评估结果，wi值可理解为评估专家对目标函数fi（X）所对应优化目标的偏好，本文改进蚁群算法模拟评估专家（等同算法中的工作单元）进行讨论，并在评估偏好上趋于一致的过程，称为“多专家综合评估算法”。该算法的关键要素和步骤说明如下：

a）评估参数X*离散化处理

对于不同的方案，决策要素（即各舱室的位置、层高等）本身已是离散的，只需对加权系数wi（i＝1，2，…，n）进行离散化处理。设加权系数 wi取值范围为［wi0－ai，wi0＋ ai］，把该区域均分为λi个区间，则对于n个加权系数，可分为D＝λi个区间。初始时，可将对应每个权衡考虑的加权系数分布在加权区间网格内随机处，每个加权区间可代表其中一位评估专家初始的权衡倾向。

b）赋予每个加权区间吸引度 tj，j＝1，2，…，D

将加权范围离散化成D个小区间后，赋予每个加权区间吸引度 tj（j＝1，2，…，D），吸引度值的大小反应了评估专家进行评估时，对采用该加权区间进行评估的认可度。

在初始时，可将每个加权区间的吸引度设定值：tj0，j＝1，2，…，D。当每个评估单元对各个方案进行评估后，各评估单元间通过“交流”将会影响各自的权衡倾向，这个过程可在评估算法中通过对各区间吸引度的修正来实现。

式中，Δtj反映了初始加权系数位于j区间的评估单元通过与其它区间采用的加权系数相比较后，对该加权区间的重新考虑；参数ρ表示引吸度的消逝程度，可选取为小于1的常数；Lj表示本次循环中评估单元j在当前加权区间j进行评估与原始认同的加权区间j0进行评估比较得出综合评估指标的变化量，可定义为：

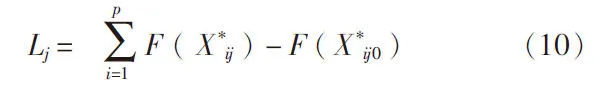
式中，p表示待评估的布置方案总数；X*ij表示评估单元j当前所认同的加权系数区间（序号设为j）与评估布置方案i组合而成的综合评估函数的输入变量；X*ij0表示评估单元j初始所认同的加权系数区间（序号设为j0）与评估布置方案i组合而成的综合评估函数的输入变量。

c）方案的吸引度 μj，j＝1，2，…，p

方案的吸引度大小反映了所有评估单元对某个方案的认可度。初始化时可将每个方案的吸引度设为定值，在进行了一个循环之后，吸引度将会发生变化，可定义为：

式中，p表示方案的总数；X*ij表示评估评估单元i当前所认同的加权系数与布置方案j组合而成的输入变量；X*ij0表示评估单元i初始所认同的加权系数与评估布置方案j组合而成的综合评估函数的输入变量。

d）各专家认同的当前加权系数的变化

在进行完每一循环之后，各个评估单元可能由初始位于的加权系数区间进行转变。定义转变的概率如下：

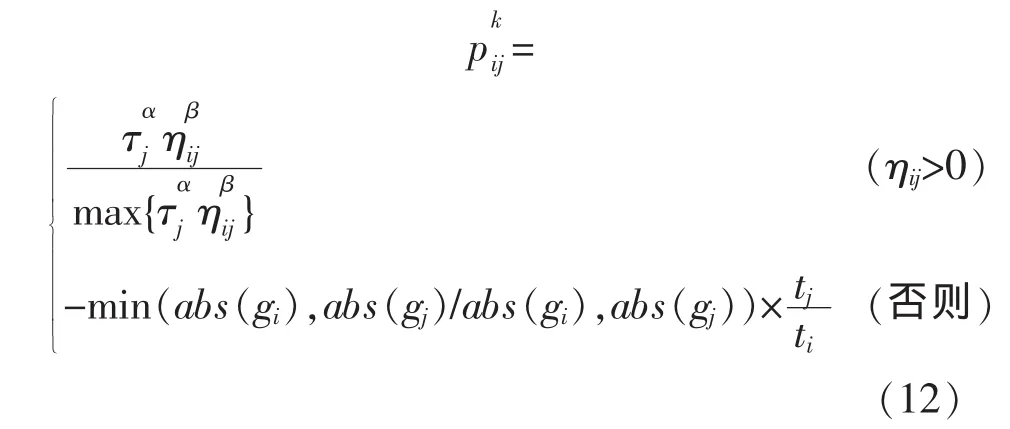
式中，α、β分别表示吸引度和期望值对专家倾向的加权系数区间变化的影响大小，一般都设为小于1的常量；gi为在评估区间i内对各个布置方案进行评估最大的平均值，可按下式进行计算：

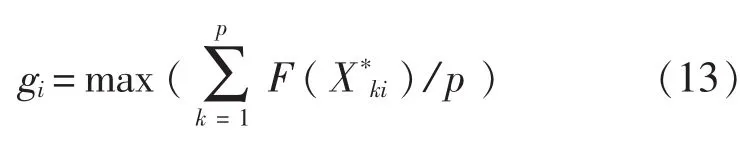
式中，p为总布置方案数目；ηij定义评估单元对评估加权系数从加权区间i转至区间j的期望值，可按下式进行计算：

对于ηij＜0的情况，为避免不再采用加权区间j进行评估的情况出现，设置了一定的跳转概率，并以负数表明，当加权区间j的吸引度越大，跳转的概率也越大。

多专家综合评估模型根据一轮评估循环之后所得的各个加权区间的吸引度和各个方案的评估指标，对各评估单元采用加权系数进行转变，并重新评估。对于当前倾向评估加权区间i的评估单元转变倾向于加权区间j的规则为：

e）循环过程及决策依据

多专家协商多方案综合评估算法的步骤可简述如下：

（1）初始时，在每个加权区间内随机分配一个模拟专家偏好的加权系数，即算法在每个加权区间内自动生成一个评估单元，并对每个加权区间初始化相同的吸引度τ，对所有待评估的布置方案设置相同的初始引吸度值μ。

（2）按照加权区间的次序，依次采用离散的加权系数和布置方案1的设计变量组合成综合评估变量X*，并依据多目标综合评估函数对布置方案1进行综合评估。

（3）按步骤（2）做法，依次对剩余方案进行综合评估。

（4）根据综合评估结果对布置方案按式（13）计算各加权区间对应的最大评估平均值，并根据计算结果按式（12）计算各评估单元倾向加权系数区间发生变化的概率，再根据式（15）计算各评估单元下步循环评估所倾向的加权系数区间。

（5）根据计算所得各评估单元当前所倾向的加权系数区间，在该区间内随机得出＝1的加权系数。

（6）按照步骤（2）和步骤（3）重新对各个方案再次进行综合评估。

（7）依据本次评估结果与上次评估结果对每个评估加权区间按式（9）、式（10）计算该区间的吸引度；根据式（11）更新每个方案的吸引度值。

（8）以当前计算结果重复步骤（4）～（7），作为一次循环结果。

（9）当各专家倾向的加权区间达成一致或计算达到设定次数的循环结束计算，否则重复步骤（4）～（7）。

3 多专家评估算法的应用与效果

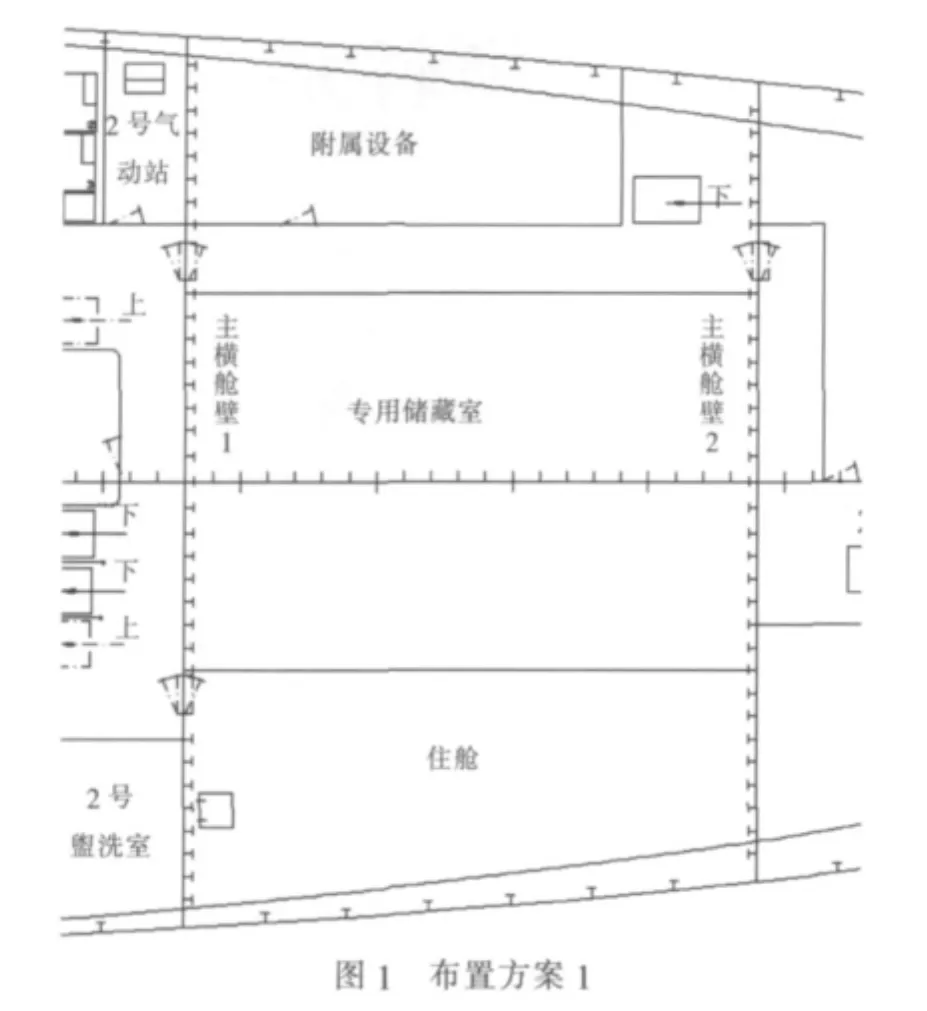
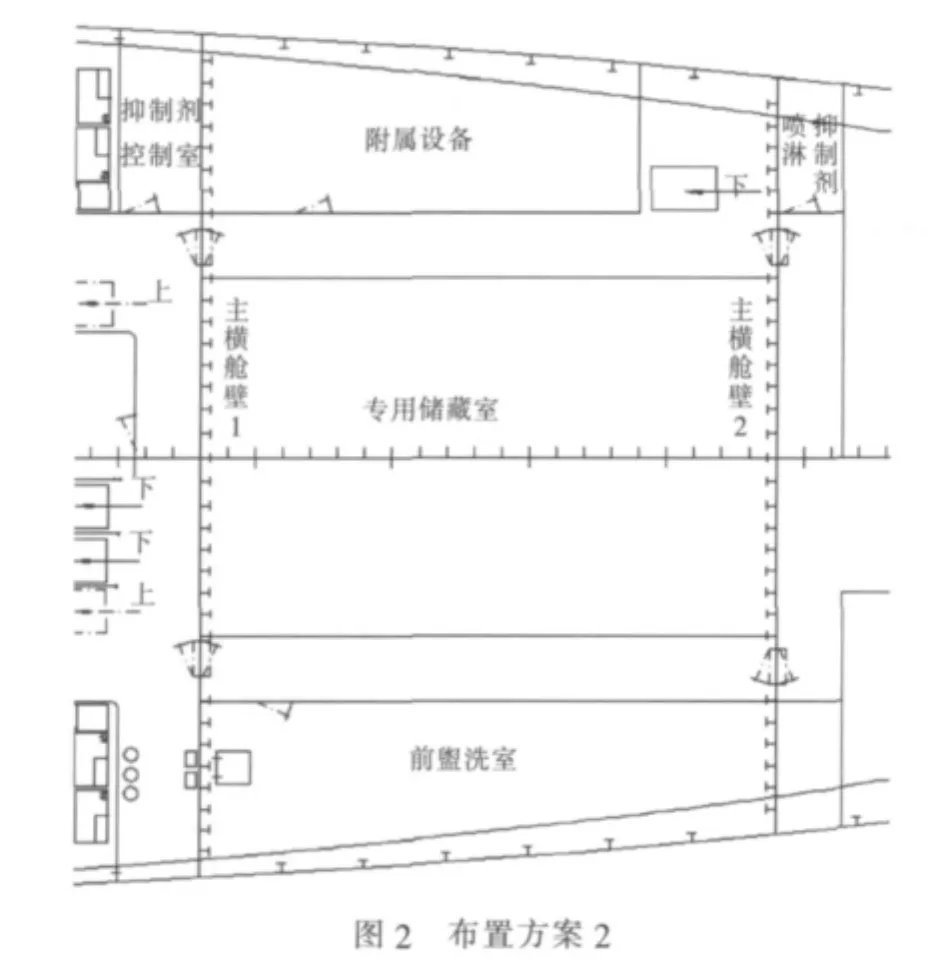
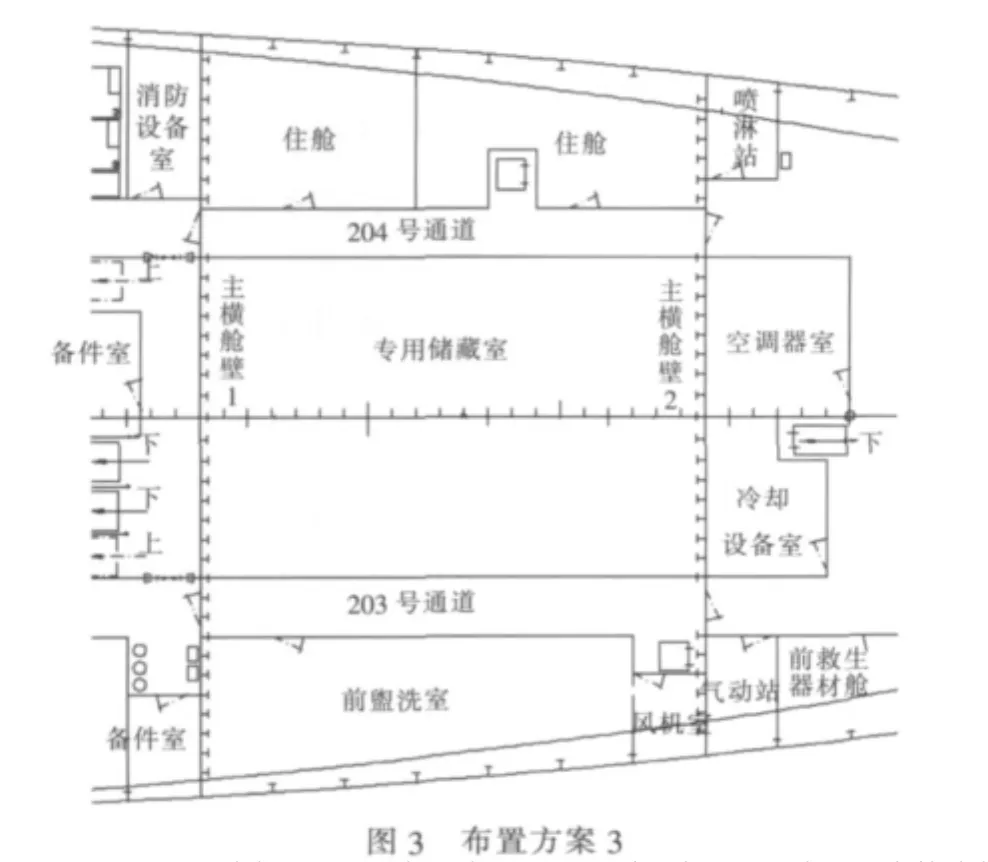
采用本文提出的多专家综合评估算法对某舰船部分区域的布置设计进行多方案综合评估，见布置方案图1～图3。图中所示的主横舱壁1与主横舱壁2的区间内，方案1设置住舱、设备舱及专用储藏室等，左舷设置贯通的纵向通道，并在左右舷各设置垂向通道，其中左舷为斜梯，右舷为直梯；方案2右舷住舱改设为盥洗室，左、右舷设置贯通的纵向通道并设置为与主横舱壁1前及主横舱壁2后的横向通道形成一体，保持其连续性。方案3也设计左、右舷贯通的纵向通道，并将左舷改设为两个住舱，并将右舷斜梯改为直梯，在右舷另增设风机室。

将该舰船2段主横舱壁间区域布置建立多目标综合评估模型，并针对各设计方案采用本文提出多专家综合算法进行评估。单目标函数包括：通道纵向通畅目标函数f1、住舱与盥洗室舒适性目标函数f2、设备舱室布置目标函数f3、垂向通道通畅目标函数f4。目标函数f1，f2，f3与前文所述相似，垂向通道的通畅目标函数f4可简化处理，并按照下式建立：

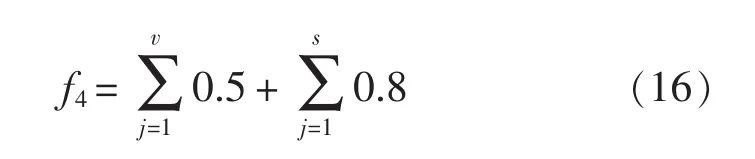
式中，v表示该区域直梯个数；s表示该区域斜梯个数。该区域多目标综合评估函数可定义为下式：

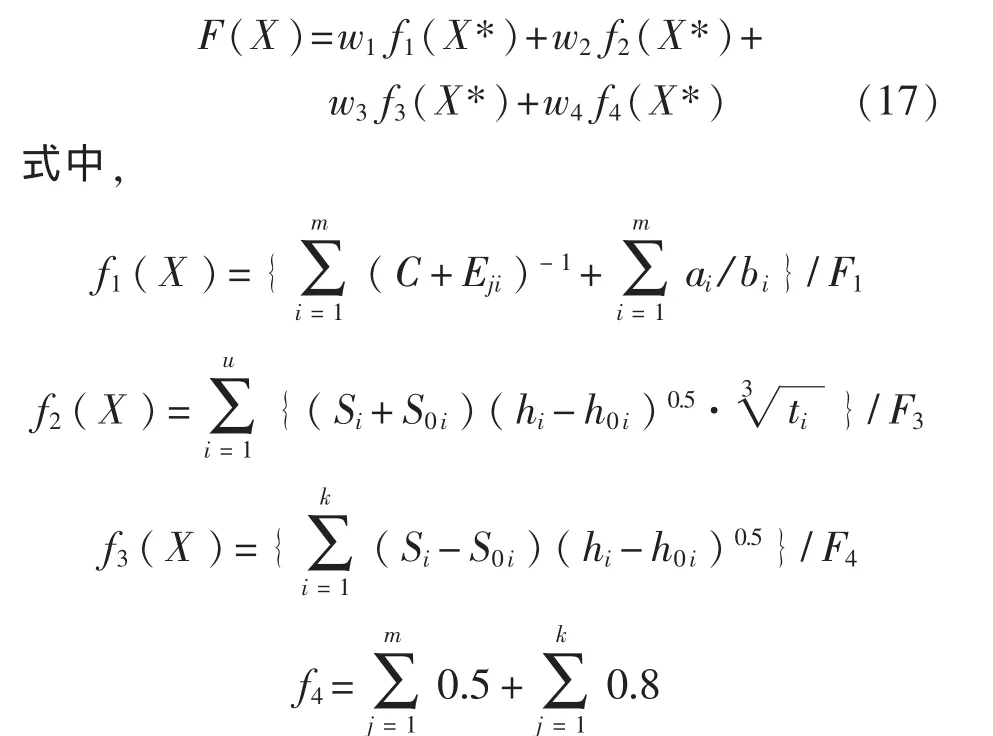
式中，f2（X）针对住舱与盥洗室的舒适度建立目标函数，如果方案没有布置士兵舱，则不考虑其的影响；t1、t2为住舱人员平均停留时间，可设为10 h，t3为前盥洗室人员平均停留时间，可根据盥洗室大小设定，本文设为5 h，S01、S02为住舱满足规定人数下居住性要求的最小面积，一般人均面积1.5～2.0 m2； f3（X）针对风机室、附属设备舱布置条件建立目标函数，为风机室最小布置面积，设为3.5 m2，S02为附属设备舱最小布置面积，设为5 m2，如果没有附属设备舱则不考虑该舱对目标函数的影响。

按前文所述的多专家综合评估算法进行评估，考虑到各评估函数的重要性，wi，i=1，2，3，4 分别设定范围如下：

w1∈［0.3-0.1，0.3+0.1］，w2∈［0.25-0.1，0.25+0.1］w3∈［0.25-0.1，0.25+0.1］，w4∈［0.2-0.1，0.2+0.1］

将 wi，i=1，2，3，4 划分为10×10×10×10 个加权区间。初始时每个加权区间的吸引度τ设为1，每个方案的初始吸引度μ也设为1。

采用多专家协商算法评估完毕后，各评估单元所倾向的加权区间大部分集中在加权区间：

w1∈［0.32，0.34］，w2∈［0.25，0.27］，w3∈［0.21，0.23］，w4∈［0.18，0.20］，在该范围内随机生成某加权系数，并使其满足=1，分别对方案1、方案2和方案3参照式（2）计算各方案的多目标评估指标。方案1 F（X*）=0.87，方案2 F（X*）=1.17，方案 3 F（X*）=1.37。由此可表明，经过多专家协商综合评估算法计算后，评估模型最终倾向方案3。