浅析导航系统不同顺序之间坐标变换的统一性
2010-11-07李成安佰勇俞利江海军潜艇学院学员3队266071
李成 安佰勇 俞利江 海军潜艇学院学员3队 266071
浅析导航系统不同顺序之间坐标变换的统一性
李成 安佰勇 俞利江 海军潜艇学院学员3队 266071
列举了在实践中导航系统中坐标变换的常用方法,指出在方向余弦阵中,应用立体解析几何分析,虽然旋转角度不是矢量,不满足平行四边形法则,但是通过一定的变换,使每轴旋转不同角度,则不同旋转顺序的坐标轴变换都可以得到相同的结果,即体现方向余弦阵不同顺序之间的统一性。给出了一种坐标变换的思路,同时也解释了导航坐标变换的意义在于其有实际的物理意义。
坐标变换;方向余弦阵;不同顺序;统一性
1 引言
现代导航设备中不论是平台式惯导还是捷联式惯导,其随着时间的推移都需要进行大量的坐标变换。旋转矢量法在解决复杂角速度变化环境下的坐标变换问题以其有效地补偿不可交换性误差而被广泛采用。同时,其根据不同的角速度变化情况通过改变一个周期内的采样次数而进行的多子样的算法和与之匹配的龙格库塔法可以大大提高坐标系变换后的精度。而作为旋转矢量法的单子样的特例,四元数法在角速度变化不复杂的情况下也有着广泛的应用,四元数法的优点在于其算法更新得快,运算量小。大多数参考书上提到方向余弦矩阵法坐标变化时都认为它的不可交换性误差导致了有限旋转不是矢量。而通过立体几何的分析可知,任何一种变换顺序都可以完成从起始坐标系到固定坐标系的坐标变换,而且彼此之间误差固定在一个相差不大的数量上。同时,可以大大减少实际中的运算量。
2 变换原理
起始如下图所示,设固定A系,经过旋转变换到达B系,(这里忽略坐标系的平动和伸缩变换,其平动和伸缩变换可以通过在变换结果上加一个固定矢量和乘一个比例因子得到)测量两个坐标系对应轴向之间的夹角,设定对应X轴之间的夹角为α,对应Y轴之间的夹角为β,对应Z轴之间的夹角为γ。

图1 固定坐标系之间的对应轴向角度
先对三个夹角的范围进行讨论:由图可知,B系的XB可以看作是以O为顶点,Z=x*tanα为母线的圆锥上的一条母线,其圆锥方程为:

设定XB轴与X轴形成的平面与YOZ平面形成的角度为θ,则可知在此XB轴的方向矢量为

同时以O点为顶点,以Y轴为轴心的圆锥方程为

通过联立方程(2)(3)可得β角的取值范围:

上式中,若tanβ=0,即β=0,则表示YB轴相对于Y轴没有变化。同时取y=1,θ=π/2,得到YB轴的方向,代入ZB轴的定义式中ZB=XB×YB可得到ZB的方向为:

其中对应于YB的两种选法,ZB有两种对应。这样,三个轴向都确定下来,α角可以任意选定,β角可以在范围内任意选定,对于选定的α和β,都有固定的γ与之对应。
接下来对各个顺序的坐标变换进行说明。下面以X—Y—Z的顺序展开说明:其旋转过程如下图所示:

图2 坐标系的旋转过程
对于X轴,由三垂线定理可以知道
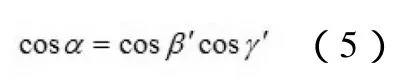
对于Y轴,其变化过程如下图所示:

图3 Y轴的变化过程
由三垂线定理和余弦定理可得
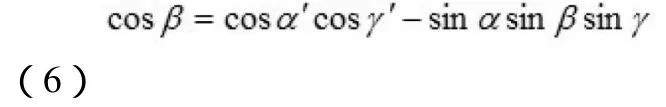
对于Z轴,同理可得
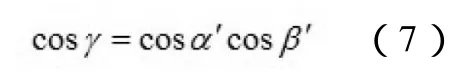
其中α’、β’、γ’分别为原坐标系绕着X、Y、Z旋转地角度。联立方程(5)(6)(7),就得到了关于X—Y—Z的变换顺序的三个旋转角度。

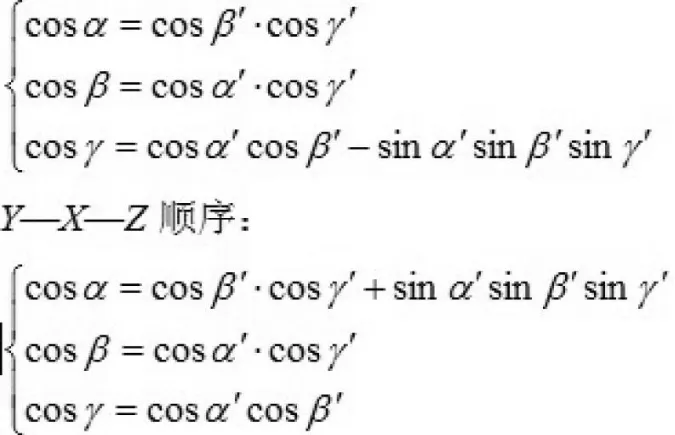
这样,就得到了终止坐标系B系相对于A系变换后对应于六种旋转方式的每个轴的转量。然后通过比较一个固定的矢量如在A系的(1,1,1),来比较各种旋转顺序的误差大小。
3 实验仿真
通过matlab进行运算,设定初始条件下三个轴向上的对应夹角分别是α=12. 3°,β=14.6°,γ=19.1°。那么通过上面各个方程的迭代,得到如下表所示,其相对误差的标准为取第一种变换方式,其他变换的结果与这种方式进行比较,如在试验中,取相对误差的标准是X—Y—Z顺序的误差限。
经过分析比较,各种变换方式其误差相差不多,而误差的造成主要是因为非线性三角方程时算法的误差引入的,与其方程本身无关。
再进行大角度的比较,α=64.3°,β =87.3°,γ=52.2°,那么通过上面各个方程的迭代,得到如下表所示,同样其误差的标准为比较原矢量在新坐标系下沿着坐标单位矢量的投影所构成的向量。
经过分析比较,当旋转角度比较大的时候(超过了5°角),其各种旋转顺序的结果的相对误差依然较小。
再进行连续的比较,当坐标系B系做一个连续的变化的时候,其相对误差随着角度的变化的趋势如下图所示。

图4 各种旋转方式的相对误差随角度的变化趋势
由上图可知,随着角度的增加,其相对误差基本处于不变的状态,而且其值趋近于零。所以,由此可以看出,各种旋转方式在坐标旋转的问题上可以看成是等价的。而导航系统中通常采取的Z—Y—X旋转顺序,是根据其拥有的物理意义来确定的,即航向角,纵摇角,横摇角。
4 结束语
本文从立体解析几何的角度出发,通过测量旋转前后的坐标系的对应轴之间的夹角,得到不同顺序下的旋转角度,讨论了不同的旋转顺序对结果的影响。在模拟仿真时,先讨论了各种变化下其坐标轴夹角的取值范围,然后根据不同的旋转情况进行了小角度,大角度,连续情况下的探讨,得到了在固定始终坐标系的情况下,不同旋转顺序在效果上时等价的。并且因为这种直接测量对应轴的角度来确定旋转角度,进而确定坐标的方法,与坐标系的运动过程无关,只与初始最终两个状态量有关,而且运算量较小,其精度主要取决于非线性方程组的算法误差,并无原理性误差。因此可以为合适的精度下的坐标转换方法提供一种思路。同时导航系统中通常采取的Z—Y—X旋转顺序,也是根据其拥有的物理意义来确定的,即航向角,纵摇角,横摇角。

表1 小角度旋转后各种坐标变换顺序的结果和相对误差
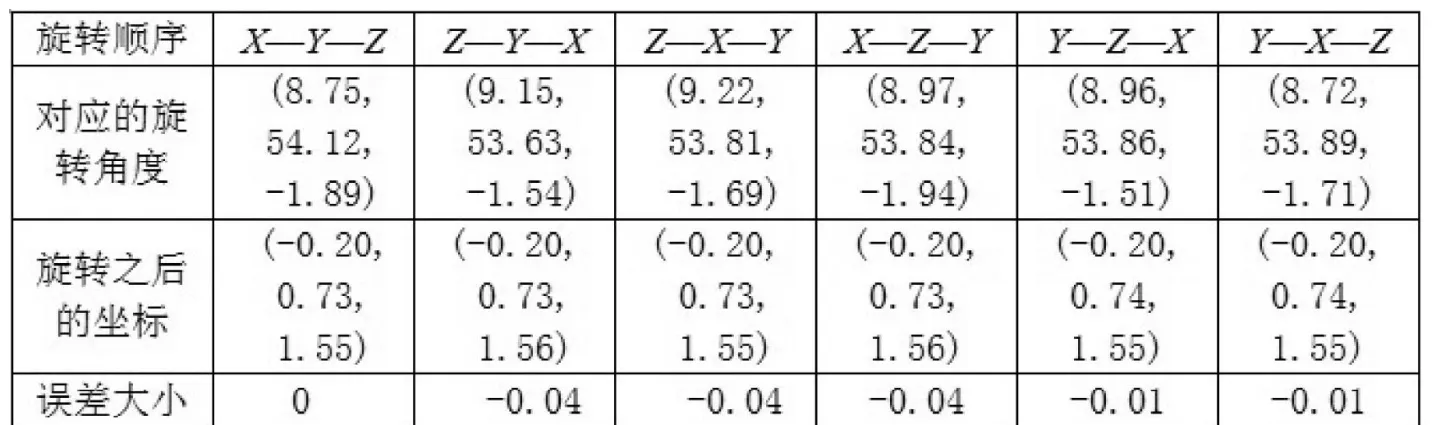
表2 小角度旋转后各种坐标变换顺序的结果和相对误差
[1]刘延柱. 陀螺力学(第三版)[M]. 科学出版社.2009.
[2]陈杰. Matlab 宝典[M]. 电子工业出版社.2007.
[3]陆珏,陈义,郑波. 总体最小二乘方法在三维坐标转换中的应用[J]. 大地测量与地球动力学.2008年第5期,26~30页.
[4]严新生.一种有效地坐标变化残差处理法[J].测绘通报.2008年第11期,55~58页.
[5]柯金朴.空问三维坐标转换原理及实现[J]. 江西测绘.2008年第3期,34~37页.
[6]陈勇.基于等效旋转矢量法的捷联惯导系统仿真[J].淮阴师范学院学报.2007年第4期,45~48页.
[7]李莹.基于飞行仿真平台的相关坐标变换模型[J].沈阳航空工业学院学报. 2005年第4期,21~26页.
[8]程连柱.几种常用的GPS坐标转换方法[J]. 计算技术与自动化.2008年第4期,16~19页.
10.3969/j.issn.1001-8972.2010.16.152
李成(1985.08—),男,海军潜艇学院导航、制导与控制专业在读研究生。
