大型桥墩的温度场及温度应力的有限元分析

2010-11-06舒开鸥

山西建筑 2010年5期

舒开鸥

0 引言

桥墩是桥梁结构最主要的受力构件,是一种大型混凝土构件。置于自然环境中的大型桥墩,长期经受自然界气温的变化等剧烈作用。由于混凝土的热传导性能差,周围环境气温等作用将使桥墩表面温度迅速上升(降低),但桥墩内部温度仍处于原来状态,在桥墩中形成较大的温度梯度,桥墩各部分处于不同的温度状态,根据热胀冷缩的原理,将产生温度变形。当桥墩的内、外约束阻碍这种变形时会产生相当大的温度应力,温度应力(尤其是拉应力)达到混凝土的强度极限时,桥墩就会开裂。

图1是武汉长江大桥武昌岸十一号桥墩(陆上)。从图1中可以看出,在桥墩的底部有三条裂纹,其中①号为主裂纹,一直延伸至地下,并且还在向上扩张,长度达3 m～4 m,裂纹宽达1.5 cm,从南北立面裂纹位置对比来看,可能为前后贯穿裂纹,另外,②号,③号裂纹也在不断生长扩张之中。这类桥墩裂纹很大程度上是由年、月温差产生的深层裂纹,一旦失稳将以很快的速度进行扩张,直接导致桥墩的整体性破坏。桥墩上部分布有因温度应力所引起的不规则的龟裂纹,其分布并无规律,但大多分布于混凝土表层,且为竖直走向。这种裂纹很大程度上是寒潮侵袭等原因导致外表面温度突然下降,外部的收缩强度和速度都明显高于内部,从而在桥墩外部产生很大的拉应力所引起。

本文将采用有限元分析软件ANSYS对大型桥墩的温度场及温度应力进行数值仿真,进而分析环境气温对桥墩温度场及温度应力的影响,探求在温度突变情况下桥墩的开裂机理,总结类似的大型混凝土温度场和温度应力变化的一般规律,提出保护方案及建议。

1 用ANSYS对温度场和温度应力进行分析

1.1 几何模型及网格生成

由于桥墩自身、边界条件及荷载工况均具有对称性,在实际计算中将桥墩的1/4作为计算模型。

用ANSYS模拟桥墩的温度场时,采用Termel Solid8 Node70单元类型,网格划分采用定义网格边长为0.4 m的Sweep方法(见图2)。

模拟温度应力时,采用Coupled Plane13单元类型,网格划分采用定义边长为0.2 m的 Map网格(见图3)。

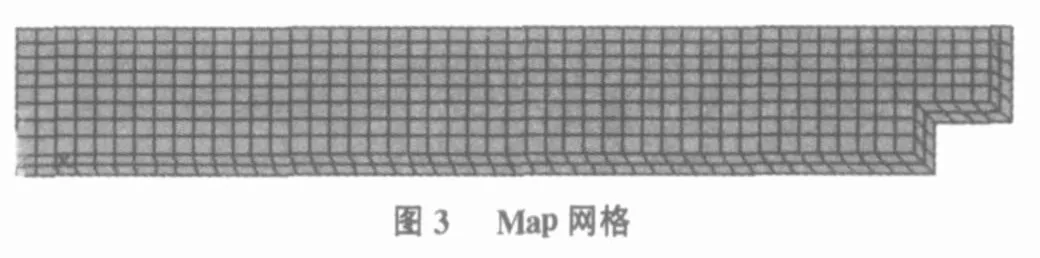
1.2 计算参数的选取

1.2.1 墩体混凝土的材料参数

弹性模量:2.5e10 Pa,泊松比:0.167,密度:2 400 kg/m3,导热系数:1.6 W/(m·℃),比热容:1 k J/(kg·℃),热膨系数:8e-6 ℃。

1.2.2 环境气温

环境气温见表1。

表1 环境气温

空气的对流换热系数 α=8 W/(m2·℃),寒潮时空气的对流换热系数α=30 W/(m2·℃)。

1.3 计算结果与分析

限于篇幅,只对 1月与 7月进行温度场模拟(见图4,图5)。由于寒潮的影响,冬天气温往往会骤降,此时表层混凝土的温度应力表现为拉应力,且应力值最大。故本次研究只模拟1月末温度骤降10℃,并持续1 d后,温度应力的分布情况(见图6)。

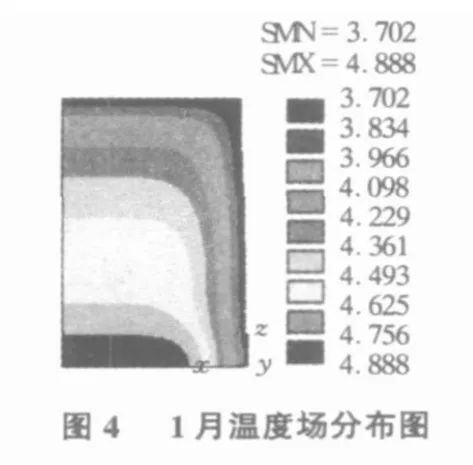
由图4,图5可以看出,由于混凝土的导热性能很差,故桥墩表层的温度与环境气温接近,而内部温度则对环境气温并不敏感。当温度持续1 d降低10℃后,由于混凝土的导热性能差,内外温差相差很大,导致温度应力的产生。

由图6可以看出,桥墩表层混凝土受到的拉应力最大为2.68 MPa,足以使表层混凝土开裂,而内部混凝土则只受到最大为0.5 MPa的压应力。

2 结论与建议

2.1 环境气温对混凝土温度场的影响

由于混凝土导热性能较差,在较短的时间内,表层温度随环境气温变化很快,而内部温度几乎不会发生变化,混凝土内部将产生很大的温度梯度,在环境气温和空气对流换热系数发生突变时表现得尤为明显。从本次模拟的情形来看,当环境温度突降10℃,空气对流换热系数从8 W/(m2·℃)突增至30 W/(m2·℃),并持续1 d时,桥墩表层0.3 m～0.7 m厚度范围内的温度变化较为剧烈。

2.2 环境气温对混凝土温度应力的影响

在环境气温突降、空气对流换热系数激增的情况下,混凝土表层将产生相当大的拉应力,由于混凝土的抗拉强度较小,因此这种天气状况很容易导致混凝土开裂,若这种开裂仅存在于混凝土表面,而且杂乱无章,其尺寸也较小,对结构的安全不会有大的影响,但是若这些裂纹(尤其是纵向裂缝)首尾相接,就会形成一些长度很长的裂纹,在交变的温度应力作用下,这些长裂纹有可能继续扩张并贯穿墩体,而将整个桥墩劈裂成若干柱形体,桥墩就有失稳破坏的危险。