基于沈珠江双屈服面模型理论的土体弹塑性模型

沈广军

(河海大学岩土工程研究所,江苏南京 210098)

基于沈珠江双屈服面模型理论的土体弹塑性模型

沈广军

(河海大学岩土工程研究所,江苏南京 210098)

由于常用的邓肯 E-μ、E-B模型的经验公式不能同时很好地反映粗粒土三轴剪切试验结果低围压剪胀、高围压剪缩变形特点,邓肯 E-μ、E-B模型基于的广义虎克定律不能反映土体剪胀剪缩特性,所以笔者应用笔者发现的三轴剪切体变规律和沈珠江双屈服面模型理论相结合建立了基于沈珠江双屈服面模型理论的弹塑性模型,该模型能够很好地反映土体的剪胀剪缩特性,能够准确地拟合等围压剪切试验结果,能够很好地预测等应力比路径,等平均主应力路径,等大主应力,小主应力减小路径,小主应力和剪应力同等减小的应力路径的试验结果。

土体;三轴试验;邓肯模型;体变规律;沈珠江双屈服面理论;弹塑性模型

0 引言

粗粒土分布广泛,储量丰富,具有压实性能好、填筑密度大、抗剪强度高、就地取材、少占农田、施工快速、施工时受雨季影响小等优点,在高土石坝、高速公路、高速铁路等工程中得到广泛应用。但目前对粗粒土力学性质研究的还不够深入,其研究成果大多延用砂土材料的研究成果。与砂土相比,堆石料在受力过程中易剪胀、颗粒易破碎从而表现出不同的力学性质。反映这些性质,建立适用于粗粒土的本构模型一直是工程界、学术界努力的方向。

现在广泛采用的邓肯 E-μ、E-B模型[1,2],由于其经验公式不能同时准确地描述粗粒土低围压时剪胀变形、高围压时剪缩变形,其理论基于广义虎克定律不能反映土体剪胀剪缩特性。所以有必要加以改进和完善以期更好地描述土体受力变形情况。笔者将采用笔者提出的能同时较好地描述土体在等围压剪切条件下低围压时剪胀变形、高围压时剪缩变形的体变公式改进邓肯模型的体变公式,并用沈珠江双屈服面模型改进虎克定律建立基于沈珠江双屈服面理论的弹塑性模型。

1 笔者所提经验公式

笔者根据大量的等围压三轴排水 (排气)剪切试验结果提出的经验公式形式为:

不同围压时参数D相差不大,取 D为不同围压的平均值。参数 f随围压的增加而减小,可以很好地表示成 f=G-Flg(σ3/Pa),其中 G、F为试验参数。

2 基于沈珠江双屈服面理论的弹塑性模型

将笔者所提能同时准确反映低围压剪胀、高围压剪缩变形的经验公式和能反映土体剪胀剪缩特性的沈珠江双屈服面模型理论相结合,形成基于沈珠江双屈服面模型理论的弹塑性模型。该模型可以反映土体的剪胀剪缩特性,也可以准确地反映土体低围压剪胀变形、高围压剪缩变形。下面开始建立该模型。

该模型主要有 10个参数,分别为 c、φ(或φ0、Δ φ)、Rf、K、n、G、F、D、Kur、μur,参数确定方法与邓肯E-μ模型相似。参数确定采用等围压三轴剪切排水 (排气)试验,该试验简单易行。

3 基于沈珠江双屈服面理论的弹塑性模型的验证

主要从两个方面加以验证:一方面是普通应力路径的验证,这方面的工作笔者做了很多,验证了50组不同学者进行的粗粒土、细粒土的干样、饱和样等围压排水 (排气)剪切试验结果,验证结果表明均很好地满足笔者所提出的规律;另一个方面是复杂应力路径的验证,即用等围压剪切试验确定的模型参数计算其他应力路径的变形结果,然后与实测结果相比,验证模型的准确性,由于这方面的全套数据不多,所以笔者能收集到的数据也不多。下面笔者主要验证一些复杂应力路径的预测效果。

3.1 利用糯扎渡大型三轴剪切试验结果验证本文所提本构模型

使用糯扎渡高心墙堆石坝 I区主堆石料普通大型三轴剪切试验结果和典型复杂应力路径大型三轴试验结果[6]对本文模型进行验证。试验具体的复杂应力路径如图 1所示。

图 1 三轴试验复杂应力路径

首先根据常规三轴压缩试验结果确定模型参数(见表 1)。并对该路径进行模拟计算,然后对选择的典型复杂应力路径试验,使用笔者所提的模型预测计算这些应力路径上的应力应变关系,同试验结果进行了对比分析。

表 1 模型参数

图 2为等围压剪切应力路径的模型计算结果,从模型计算结果和试验结果的对比可以看出,εv-ε关系曲线模拟的还是比较准确的,且能同时准确反映低围压剪胀变形、高围压剪缩变形。计算的 (σ1-σ3)-εa关系曲线有一些误差。可能是由于参数确定不准造成的。

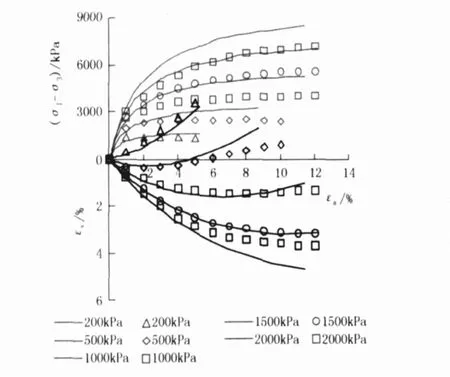
图 2 等围压剪切路径的模型计算结果

图 3为本文模型对复杂应力路径试验 D1～D3的预测计算结果。该路径起始段是等应力比 (η=q/p=1)路径,当σ3分别达到 300、800、1400 kPa时改为常规三轴剪切试验并直到试样发生剪切破坏。该应力路径实际上是不等压固结三轴压缩试验的应力路径。对于 p-εv关系,本文模型计算的体变数值稍微偏小,计算的规律基本相符。对于 q-εs关系,前期计算结果较好,后期有些偏差,偏差与等围压剪切路径类似。

图 4为本文模型对复杂应力路径试验D4和D5的预测计算结果。该试验路径起始段也为等应力比(η=q/p=1)路径。但当σ3分别达到 800、1400 kPa时变化为σ1维持不变,σ3减小 (σ1-σ3)增加直到破坏的变应力比试验,从模型计算结果来看,模型计算出的体积应变数值稍小于实测结果,剪切应力的计算结果稍大于计算结果,应力变形规律基本相似。

图 5为本文模型对复杂应力路径 D6和 D7的预测计算结果。试验 D6和 D7的应力路径是一个典型的发生“卸载”破坏的应力路径 (图 10)。在该应力路径上,无论是 p还是 q均在减小,但应力比在缓缓增加。由试验结果可见,在应力发生转折的初始段,无论是 p-εv关系还是 q-εs关系都表现为卸载;但在接近破坏时,试样发生突然的破坏。在试样发生破坏时,围压σ3的值较低,试样发生显著的剪胀。

3.2 利用中密粉土三轴排水剪切试验结果验证本文所提本构模型

图 3 试验D1～D3的模型预测结果

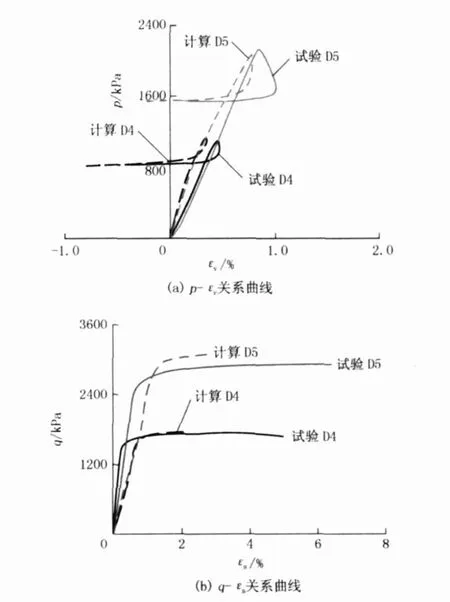
图 4 试验 D4和 D5的模型预测结果

使用济南洛口黄河大堤外的粉土普通中型三轴剪切试验结果和典型复杂应力路径中型三轴试验结果[7]对本文模型进行验证。

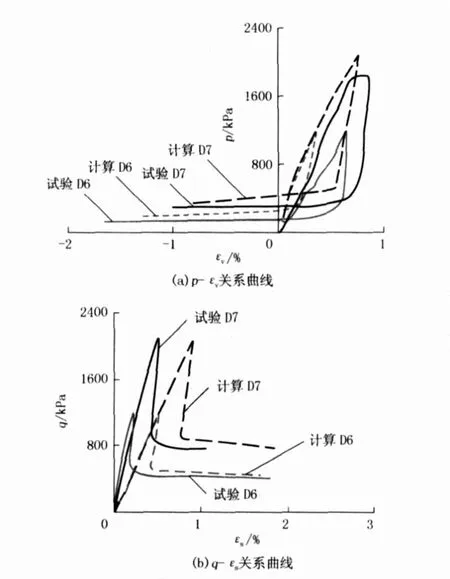
图 5 试验 D6和 D7的模型预测结果

首先根据常规三轴压缩试验结果确定模型参数(见表 2)。并对该路径进行模拟计算,然后对选择的典型复杂应力路径试验,使用笔者所提的模型预测计算这些应力路径上的应力应变关系,同试验结果进行了对比分析。

表 2 模型参数

图 6为等围压剪切应力路径的模型计算结果,从模型计算结果和试验结果的对比可以看出,εvεa关系曲线模拟的还是比较准确的。计算的 (σ1-σ3)-εa关系曲线也较准确。

图 7为本文模型对复杂应力路径试验的预测计算结果,对于等 p(p=300 kPa)应力路径,本文模型预测的体变关系非常符合实际计算结果,且能很好地反映土体剪胀特性。对于等 dq/dp(dq/dp=210、-115、-310)路径,本文模型预测的体变关系、轴变关系都很好地符合实际情况。

3.3 利用正常固结粘性土三轴排水剪切试验结果验证本文所提本构模型

使用黄河小浪底土坝西河清料场心墙粘性土普通三轴剪切试验结果和典型复杂应力路径三轴试验结果[8]对本文模型进行验证。

图 6 等围压三轴剪切预测结果和试验结果

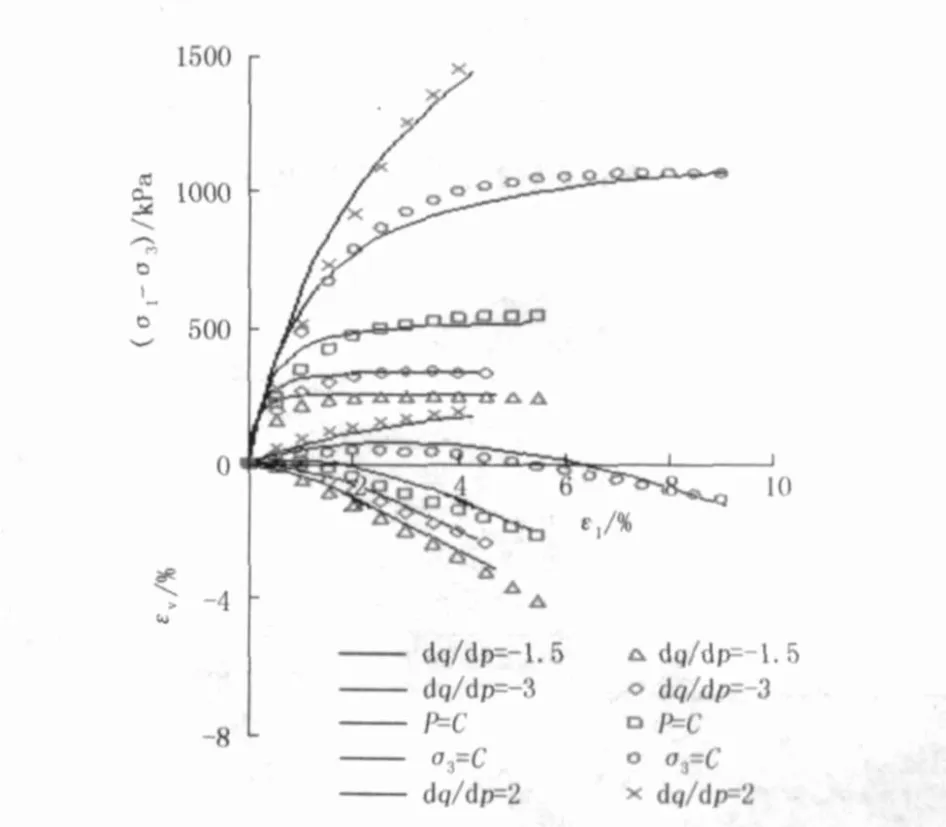
图 7 固结压力为 300 kPa时,不同应力比的预测结果和试验结果

首先根据常规三轴压缩试验结果确定模型参数(见表 3)。并对该路径进行模拟计算,然后对选择的典型复杂应力路径试验,使用笔者所提的模型预测计算这些应力路径上的应力应变关系,同试验结果进行了对比分析。

表 3 模型参数

图 8为等围压剪切应力路径的模型计算结果,从模型计算结果和试验结果的对比可以看出,εvεa关系曲线模拟的还是比较合理的。计算的 (σ1-σ3)-εa关系曲线也较准确。

图 9为本文模型对复杂应力路径试验的预测计算结果,对于等 p(p=300 kPa)应力路径,本文模型预测的体变关系比较符合实际计算结果。且能较好地反映土体剪缩特性。对于等 dq/dp(dq/dp=01375、0175、115、2125)路径 ,本文模型预测的体变关系、轴变关系都很好地符合实际情况。

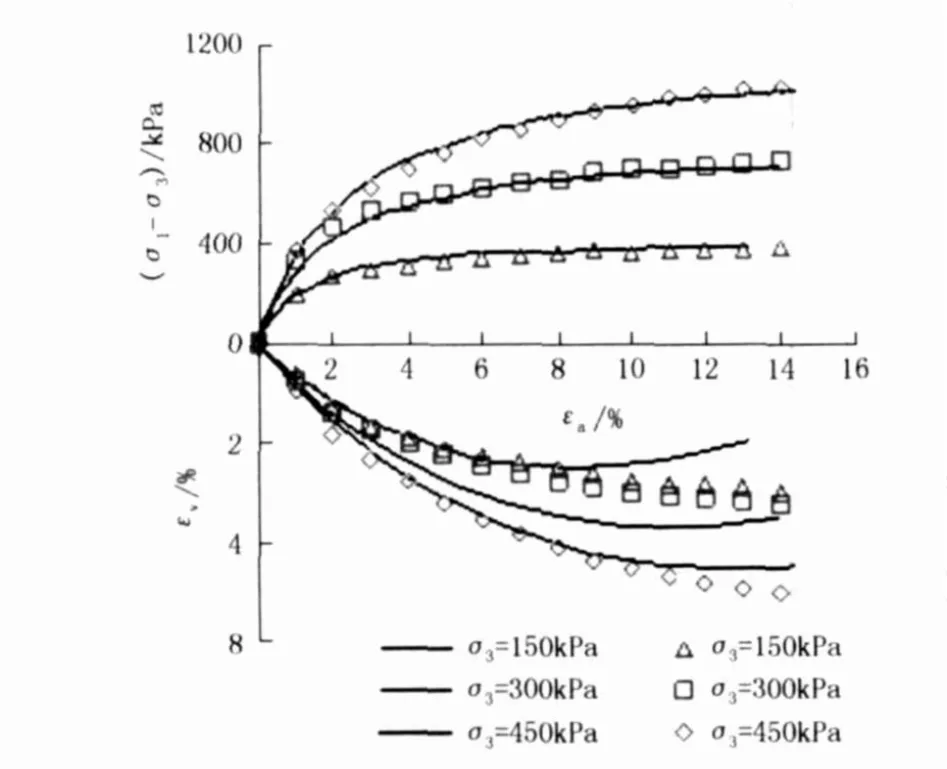
图 8 等围压三轴剪切预测结果和试验结果

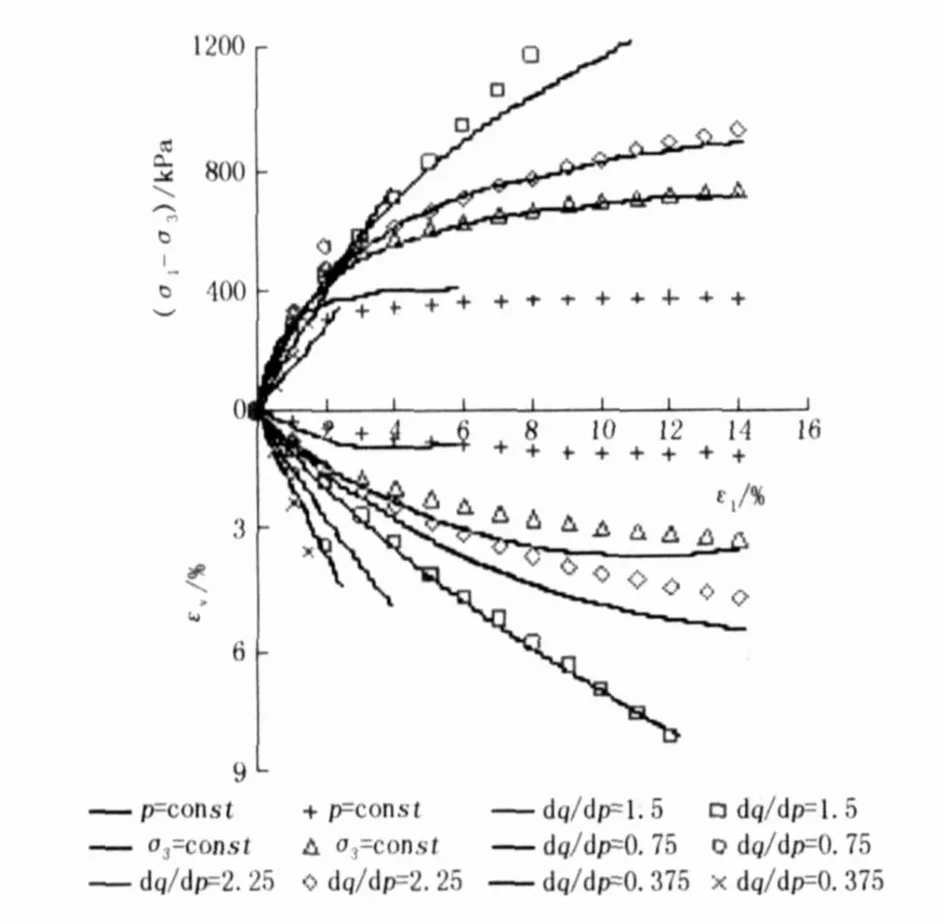
图 9 固结压力为 300 kPa时,不同应力比的预测结果和试验结果

4 结论

笔者主要对邓肯模型进行了两方面的改进,改进之后建立了基于沈珠江双屈服面模型理论的弹塑性模型,该模型具有以下一些特点。

(1)该模型基于笔者所提的体变公式,该经验公式能很好地反映等围压三轴排水 (排气)剪切试验结果。该经验公式能准确反映低围压剪胀、高围压剪缩变形的试验结果,也能准确反映低围压、高围压均剪缩变形的试验结果。

(2)该模型基于沈珠江双屈服面模型理论,该理论能够反映土体的剪胀剪缩特性。

(3)该模型确定参数仅基于等围压三轴排水(排气)剪切试验,参数确定简单可靠。

(4)该模型能够较准确地反映土体剪胀剪缩变形,能够较准确地反映不同应力比路径的变形情况。该模型能够较准确地反映土体接近破坏时的受力变形情况。

(5)该模型特别适用于粗粒土,也能较好地应用于细粒土,该模型是一个很有发展前景的模型。

[1] Duncan J M,Chang C-Y.Nonlinear Analysis of Stress and Strain in Soils[J].Journal of the SoilMechanics and Foundations Division,Proceedings of the American Society of Civil Engineer-ing,1970,(5):1629-1653.

[2] Duncan J M,Byrne P,Wong K S,et al.Strength,Tress2strain and BulkModulus Parameters for FEA of Stress andMovements in SoilMasses[R].ReportNo.UCB/GT/80-01.California:Cal-ifornia University,1980.

[3] 沈珠江.土体应力应变分析中的一种新模型[A].第五届土力学及基础工程学术讨论会论文集[C].北京:中国建筑工业出版社,1990.101-105.

[4] 沈珠江,王剑平.土质心墙坝填筑及蓄水变形的数值模拟[J].水利水运工程学报,1988,(4).

[5] 沈珠江,王剑平.横山水库土石坝有效应力应变分析[J].水利学报,1990,(4).

[6] 贾延安.复杂应力路径下堆石体本构模型的比较验证[D].北京:清华大学,2006.

[7] 张明义,邓安福.不同应力路径加荷时粉土的应力应变关系[J].青岛理工大学学报,1992,13(2):1-7.

[8] 徐光明.应力路径对击实粘土强度和变形的影响[D].南京:河海大学,1988.

Elasto Plasticity ConstitutiveM odel of Soils Based on Shen Zhu2j iang’sDouble-yield Surface Theory

SHEN Guang-jun(Geotechnical Institute of HohaiUniversity,Nanjing Jiangsu 210098,China)

Empirical formula ofDuncanE-μ、E-Bmodel can not s imultaneously reflect the low confining pressure dilat- ancy deformation and high confining pressure shear contraction defor mation in coarse-grained materials tri-axial shear test,and generalized hooke’s law,on which DuncanE-μ,E-Bmodel is based,are not able to reflect the dilatancy charac-teristics of soils,so a new elasto plasticity constitutivemodel based on Shen Zhu2jiang’s double-yield surface theory is built bymeans of combining the volumetric strain laws presented by writer and Shen Zhu-jiang’s double-yield surface theory.Thismodel can well reflect the soil dilatancy characteristic,accurately fit equal confining pressure shear test results,and can predict the test resultsof equal stress ratio path,equal average principal stresspath,equal large principal stress,minor principal stress reduction path,equalminor principal stress and shear stress reduction path and so on.

soil;tri2axial test;Duncan model;volumetric deformation law;Shen Zhu2jiang’s double2yield surface theo-ry;elasto2plasticity constitutive model

TU43

A

1672-7428(2010)01-0040-05

2009-11-14

沈广军 (1979-),男 (汉族),江苏扬州人,河海大学博士研究生,岩土工程专业,从事岩土材料特性、本构关系和数值计算的研究工作,江苏省南京市,shen_gj@sina.com.cn。