New convergence theorems for Newton-like-iterative methods

WU Min

(School of Science,Zhejiang U niversity of Science and Technology,Hangzhou 310023,China)

New convergence theorems for Newton-like-iterative methods

WU Min

(School of Science,Zhejiang U niversity of Science and Technology,Hangzhou 310023,China)

Newton-like-iterative methods proposed by T.J.Ypma are obtained by using an iterative method to solve Newton-like equations.In the early paper of Ypma,the theory of inexact Newton methods was applied to study the convergence of Newton-like-iterative methods.Unlike earlier results,new local convergence theorems for Newtonlike-iterative methods by applying the theory of inexact Newton-like methods is proposed in this paper,which is seemed simpler and clearer.Moreover,the analysis is carried out in affine invariant terms.

nonlinear equations;Newton-like methods;Newton-like-iterative methods;inexact Newton method; inexact Newton-like methods;affine invariant

1 Introduction

Newton-like methods for solving the system of nonlinear equations

have the general form

where skRNis the solution s of the system of linear equations

where Ak L(RN)is some nonsingular approximation to the Fr chet derivative f (xk)of f at xk.

Moreover,L(RN)is the set of all bounded linear mappings from RNto RN.

If xkin Eq.(2)is an approximate solution of Eq.(3),obtained by using an iterative method to solve the linear equations,then we refer to the resulting combined method as a Newton-like-iterative method. Such methods have received much attention in Refs.[1-4].In Ref.[5],T.J.Ypma introduced this method and studied its convergence results,which generalized those of Refs.[2-4].His approach is to regard Newton-like-iterative methods as inexact Newton methods[6-7],as suggested in Ref.[6].T he relevant theory is applied to produce conditions for convergence,as well as radius of convergence and rate of convergence results.

Since inexact Newton methods were proposed,there have been plentiful results concerning its local convergence[6,8-10],sem-i local convergence[11-16]and global convergence[17-18],as well as its generalizations and applications to different numerical fields[19-20].Except for convergence results for inexact Newton methods,Morini[9]and Jinhai Chen-Weiguo Li[8]considered respectively inexact Newton-like methods and their local convergence theorems under different assumptions as well.To mention the results, suppose x0is a given initial guess,and then the iterative form is as follows:

For k=0 step 1 until convergence do

Find some step skwhich satisfies

Set xk+1=xk+sk;

where kis a sequence of forcing terms and Pkis an invertible matrix for each k.It is worth noting that residuals of this form are used in iterative Newton methods if preconditioning is applied,and that Pk

changes with index k if Akdoes.Taking account of the affine invariance of inexact Newton-like methods, here we choose Pk=A-1kespecially.So the condition is

Apparently,the process is inexact Newton method if Ak=f (xk)and inexact modified Newton method if Ak=f (x0).

In this paper,we give different theorems for Newton-like-iterative methods by applying the theory of inexact Newton-like methods[8-9],which are simpler and easier to apply.We first summarize,in Section 2,the convergence results for inexact Newton-like methods given in Ref.[8]and provide a new theorem as well.In Section 3,we show that Newton-like-iterative methods are themselves inexact Newton-like methods,and then derive the corresponding convergence results in Section 4.

In what follows,I denotes the identity operator.x for x RNdenotes some vector norm of x,andA for A L(RN)denotes the subordinate matrix norm of A.T he notion S(x,r)={y RN| x-y ＜r}denotes the open ball with center x and radius r.

2 Inexact Newton-like methods

Firstly,we conclude the following convergence theorem for inexact Newton-like method from Ref. [8],which produces conditions for its local convergence as well as the radius of the convergence ball.

Theorem 2.1[8]Suppose x*is the only solution of Eq.(1)in S(x*,r).Assume that f has a continuous derivative in S(x*,r),f (x*)-1exists and f (x*)-1f satisfies the following Lipschitz condition:

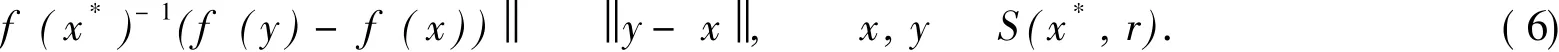
Suppose further A(x)is an approximation to the Jacobian f (x)for x S(x*,r),A(x)is invertible and such that

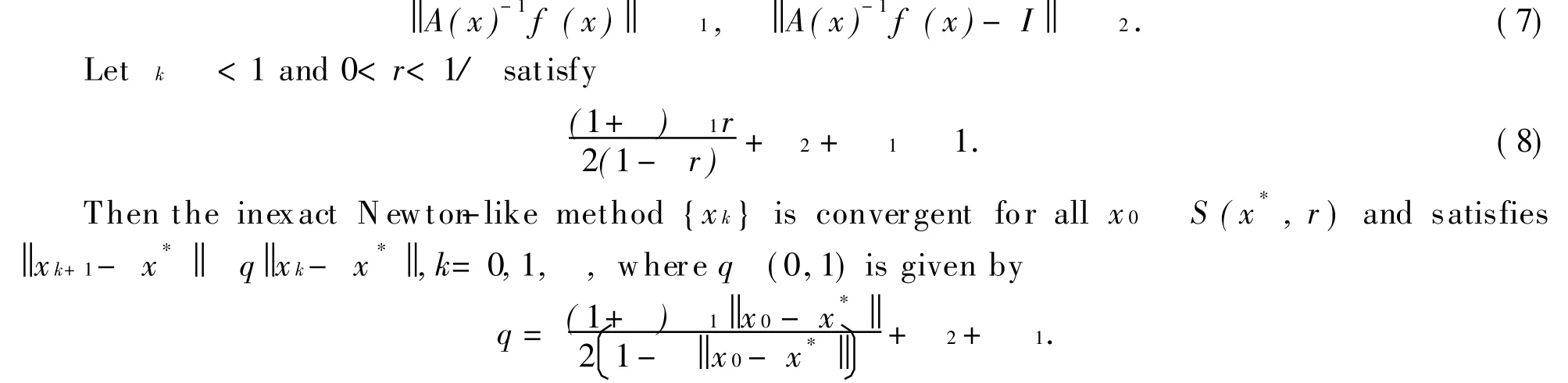
Taking A(x)=f (x),i.e., 1=1, 2=0 in T heorem 2.1,we obtain the convergent results for inexact Newton method proposed in Ref.[5].Clearly,if the equal sign holds in Eq.(8),we get the optimal radius of convergence ball for inexact Newton methods,with r=2(1- )/ (3- ).

Furthermore,let =0,then it merges into Newton s method and the estimate for the radius of convergence ball is known to be sharp[21].

In the following,we give a new convergence theorem for inexact Newton-like methods under different assumptions.

Theorem 2.2 Suppose x*is the only solution of Eq.(1)in S(x*,r).Assume that fhas a continuous derivative in S(x*,r),f (x*)-1exists and f (x*)-1f satisfies the following Lipschitz condition:

Proof Arbitrarily choosing x0S(x*,r),where r is determined by Eq.(11),q＜1 follows directly.

Since r＜1/ ,by Eq.(9)and Numann Lemma,we have that f (x)-1exists for all x0 S(x*,r)as well as

The proof is completed.

该项目使用的黑水角阀的阀套与阀芯采用机械紧固连接。由于黑水的高速冲击或流量大范围波动，连接处易出现松动，引起阀芯的震动；而阀芯材质为整体烧结硬质合金，硬度高，脆性大，在该频繁振动的工况下容易出现阀芯震裂、震碎与阀套脱离现象，使阀门失去调节作用。

3 Newton-like-iterative methods

In this section,we shall show that Newton-like-iterative methods are inexact Newton-like methods. Local convergence results follow from the above theorems.

Splitting is one of the basic principles used to generate iterative methods for solving a system of linear equations.Applying the technique to Eq.(3),and decomposing Akas

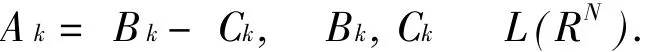
the resulting Newton-like-iterative method takes the form

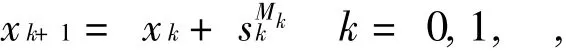
where Bkis nonsingular and the system of linear equations Bkx=d,d RN,is in some sense easy to solve.Here Mkis some positive integer and sMk kis calculated by solving successively the system of linear equations

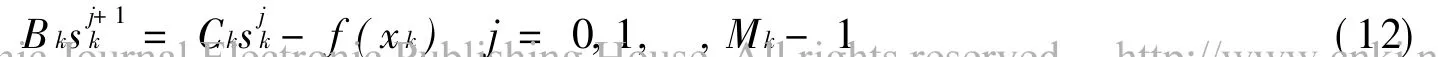
since Hk=0.T he analysis of Eq.(13)therefore generalizes the analysis of the standard Newton-like methods in Eqs.(2)and(3).

4 Convergence theorems and corollaries

Suppose the Newton-like-iterative methods are defined in Section 3.Our main result in this section is as follows.

Theorem 4.1 Suppose x*is the only solution of(1)in S(x*,r),where r satisfies Eq.(8). Assume that f has a continuous derivative in S(x*,r),f (x*)-1exists and Eq.(6)holds.Let A(x)be an approximation to the Jacobian f (x)for x S(x*,r).A(x)is invertible and Eq.(7)is satisfied. Suppose

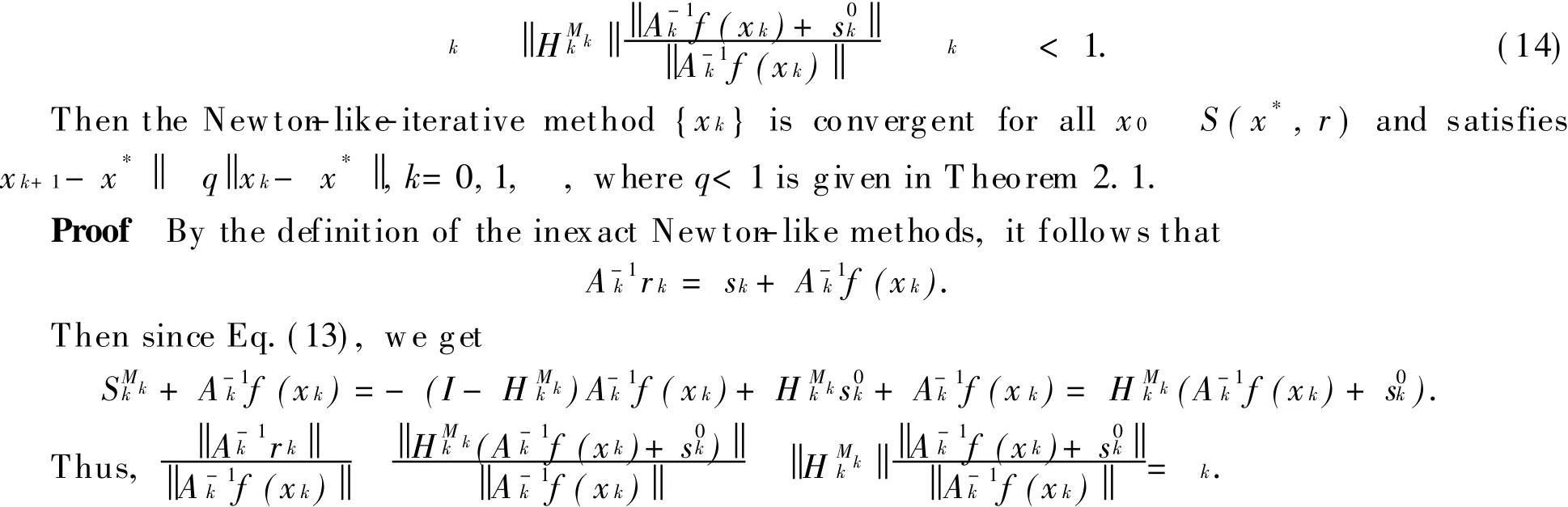
Comparing with the relative result proposed in Ref.[5],the above theorem produce simpler and clearer conditions for forcing sequence of Newton-like-iterative methods.Here,in Ref.[5], kis formulated by

Similarly,we get the following theorem from Theorem 2.2,which seems not appeared in the literature.

Theorem 4.2 Suppose x*is the only solution of Eq.(1)in S(x*,r),where r satisfies Eq.(11). Assume that f has a continuous derivative in S(x*,r),f (x*)-1exists and Eq.(9)holds.Let A(x)be an approximation to the Jacobian f (x)for x S(x*,r).A(x)is invertible and Eq.(10)is satisfied. Suppose further(14)holds.Then the Newton-like-iterative method{xk}is convergent for all x0

S(x*,r)and satisfiesxk+1-x*q xk-x*,k=0,1, ,where q＜1 is given in T heorem 2.2.

By simple deduction,we obtain the following corollary

Corollary 4.3 Let the assumptions of T heorem 4.1 hold,up to Newton-like-iterative methods,with=0,k=0,1, .Suppose that

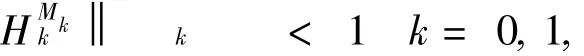
for some sequence k [0,1).T hen all the consequences of T heorem 4.1 hold.If in addition Ak f (xk),Hk＜1 and limk+Mk=+ ,then the convergence is Q-superlinear.

Remark Taking Ak f (xk)in Eq.(4),the inexact Newton-like methods merge into inexact Newton methods.The rate of convergence follows from the classical results of inexact Newton methods[6,10].

[1] BANK R E,ROSE D J.Global approximate Newton methods[J].Numer Math,1981(37):279-295.

[2] ORTEGA J M,RHEINBOLDT W C.Iterative Solution of Nonlinear Equations in Several Variables[M].New York: Academic Press,1970.

[3] RHEINBOLDT W C.Methods for Solving Systems of Nonlinear Equations[M].Philadephia:SIAM,1974.

[4] SHERMAN A H.On Newton-iterative methods for the solution of systems of nonlinear equations[J].SINU M,1978 (15):755-771.

[5] YPMA T J.Convergence of Newton-like-iterative methods[J].Numer Math,1984(45):241-251.

[6] DEMBO R S,EISENSTAT S C,ST EIHAUG T.Inexact Newton methods[J].SIAM J Numer Anal,1982(19):400-408.

[7] DENNIS J E,WALKER H F.Local convergence theorems for quas-i Newton methods[R].[2009-11-06].http://hdl. handle.net/1813/7498.Cornell Computer Science,1979.

[8] CHEN Jinhai,LI Weiguo.Convergence behaviour of inexact Newton methods under weak Lipschitz condition[J].J Comput Appl Math,2006(191):143-164.

[9] MORINI B.Convergence behaviour of inexact Newton method[J].M ath Comp,1999(68):1605-1613.

[10] YPMA T J.Local convergence of inexact Newton methods[J].SIAM J Numer Anal,1984(21):583-590.

[11] ARGROS I K.A new convergence theorem for the inexact Newton methods based on assumptions involving the second Fr chet derivative[J].Comp Math Appl,1999(37):109-115.

[12] BAI Zhongzhi,T ONG Peili.On the affine invariant convergence theorems of inexact Newton method and Broyden s method[J].Journal of UEST of China,1994(23):535-539.

[13] GUO Xueping.On semilcal convergence of inexact Newton methods[J].Journal of Computational Mathematics,2007 (25):231-242.

[14] M ORET I.A Kantorovich type theorem for inexact Newton methods[J].Numer Funct Anal Optim,1989(10):351-365.

[15] WU Min.A new sem-i local convergence theorem for the inexact Newton methods[J].Appl Math Comput,2008 (200):80-86.

[16] ZHOU Jiali,ZHANG Shuyou,YANG Guoping.A convergence theorem for the inexact Newton methods based on H lder continuous Fr chet derivative[J].Appl Math Comput,2008(197):206-211.

[17] EISENSTAT S C,WALKER H F.Globally convergent inexact Newton methods[J].SIAM J Optimization,1994 (4):393-422.

[18] SOLODOV M V,SVAITER B F.Reformulation:Nonsmooth,Piecewise Smooth,Semismooth and Smoothing M ethods[M].London:Kluwer Academic Publishers,1998.

[19] JACKSON K R.The numerical solution of large systems of stiff IVPs for ODEs[J].Appl Numer Math,1996(20): 5-20.

[20] M ARTINEZ J M,QI L.Inexact Newton methods for solving nonsmooth equations[J].J Comput Appl Math,1995 (60):127-145.

[21] WANG Xinghua.Convergence of Newton s method and uniqueness of the solution of equations in Banach space[J]. IMA J Numer Anal,2000(20):123-134.

关于Newton-like-iterative方法新的收敛性定理

武 敏

(浙江科技学院理学院,杭州310023)

用迭代法求解Newton-like法中的方程,T.J.Ypma提出Newton-like-iterative方法。在其早期的文章中,不精确牛顿法理论用来研究Newton-like-iterative方法的收敛性。与以往方法不同,今提出用不精确Newtonlike法做相关的收敛性分析,所得定理更加简单,同时具有仿射不变性。

非线性方程;Newton-like方法;Newton-like-iterative方法;不精确牛顿法;不精确Newton-like方法;仿射不变性

O241.7

A

1671-8798(2010)04-0241-06

O241.7 Document code:A Article ID:1671-8798(2010)04-0241-06

10.3969/j.issn.1671-8798.2010.04.001