基于盲数理论的深基坑抗隆起安全稳定分析

谢晓龙, 汪明武, 葛 康

(合肥工业大学土木与水利工程学院,安徽合肥 230009)

国内外对基坑的抗隆起稳定性研究极为重视,主要方法有Terzaghi-Peck法、Tschebotarioff法 、NavfacDM-7 1971 法 、Caquot-Kerisel 法,汪炳鉴-夏明耀曲线滑动法[1]等,但这些方法大多是按坑壁土体的滑坡失稳或地基承载力验算的思路推导出来的,在实际情况中存在许多问题。

近年来,国内的许多学者从不同的角度对基坑的抗隆起稳定性进行了研究,文献[2]考虑了地下水渗透力条件下的深基坑抗隆起稳定,根据土的应力强度理论推导出基坑支护抗隆起稳定问题的设计计算公式和计算方法,进行了各向异性条件下软土深基坑抗隆起稳定性的分析。到目前为止,对基坑的抗隆起稳定性分析仍存在着很多问题,因基坑抗隆起稳定性分析所涉及的岩土体物理力学参数是不确定性信息,如凝聚力、摩擦角、重度等指标往往不是一个确定值[3]。在以往的深基坑工程的分析中,大多是按照经验,而对计算参数的未确知性加以忽略,将不确定性问题作为确定性问题考虑。由于实际情况的限制和地质条件的复杂性,很难对岩土体进行大量、准确的试验,从而难以得到参数的准确值或概率分布,因此,在使用模糊数学等方法的过程中难以确定参数值合理的隶属函数,给求解带来了不便。灰色理论中多采用区间型函数来表达部分已知、部分未知的灰信息,但区间型灰数多是定义在一个区间内,且在补充信息较少的情况下灰数的白化相当困难。同理,在使用可靠型分析方法时,也需要用大量的资料来确定参数的变异性和不确定性。因此,如何全面考虑这些不确定信息,是确保基坑抗隆起稳定性分析准确性的关键。文献[4]提出的“未确知数学”概念则为这一难题提供了一条途径。因深基坑工程中参数的不确定性往往不是单一的,是多种不确定性(如模糊性和灰性)的混合体,因此,采用盲信息来表达基坑抗隆起稳定性分析中信息的随机性、模糊性、灰性及未确知性2种或2种以上不确定性的信息组合是最好的选择。

1 盲数理论

盲数是未确知数学中用于表达和处理同时具有2种或2种以上不确定性信息的数学工具[5]。对于具有不确定性的对象,其实际值并不可能总落在某个点上,应是该点附近的某个区域。

设H(I)为一系列的灰区间ai构成的区间型灰数集合,则ai∈H(I)。若αi∈[0,1],i=1,2,…,n,f(x)为定义在H(I)上的灰函数,且

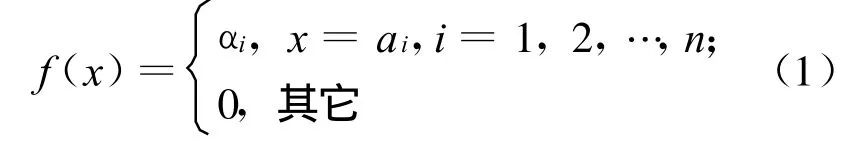
设a、b为实数,且 a≤b,称(a+b)/2为区间型灰数[a,b]的“心”,记作 Θ[a,b]=(a+b)/2。若 f(x)为盲数,表达形式同(1)式,则盲数 f(x)的期望值可以表示为:

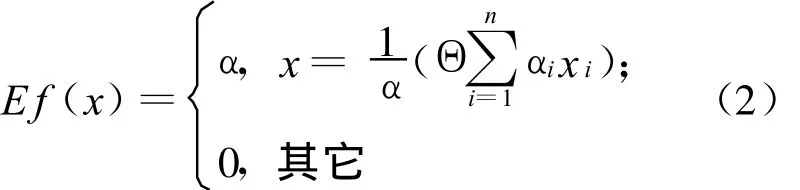
设A、B为盲数,则分布密度形式为:

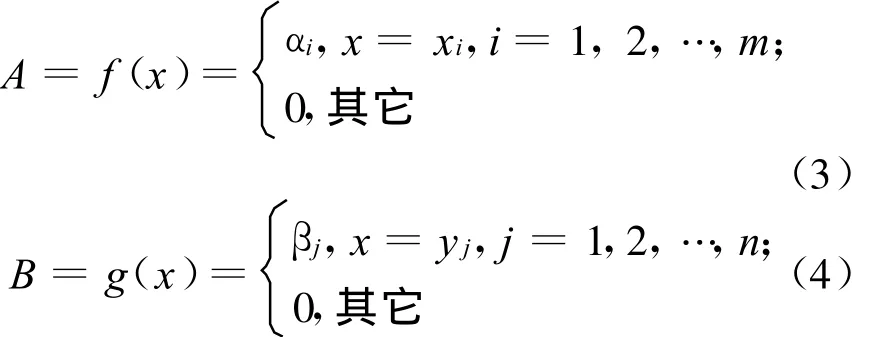
则事件A-B≥r的可靠性表示为:

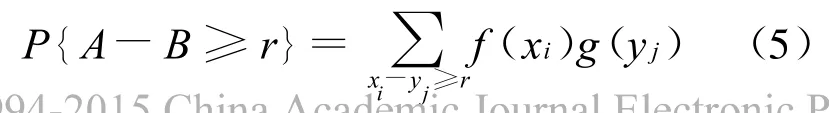
其中,B表示某一评价标准的分级阈值,一般为实数值形式;r是按实际问题要求而确定的某个已知实数,通常取r=0,则称(4)式为盲数可靠性计算模型[6]。

2 深基坑抗隆起分析模型

国内外对基坑隆起稳定问题计算大多是按坑壁土体的滑坡失稳或地基承载力验算的思路建立的。本文参照Ptandtl和Terzaghi的地基承载力公式[7],并将墙底面的平面作为求极限承载力的基准面,其滑动线形状如图1所示。

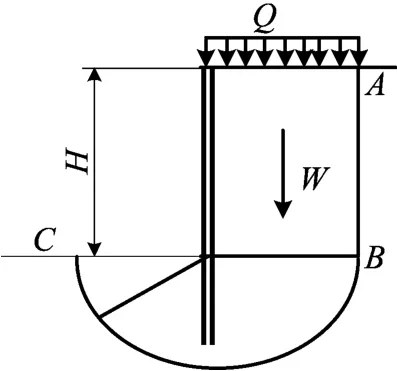
图1 坑底隆起计算图

地基承载力计算为:

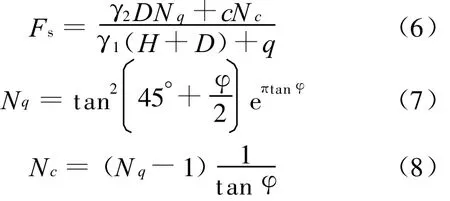
其中,D为墙体插入深度;H为基坑开挖深度;q为地面超载;γ1为坑外地表至墙底、各土层天然重度的加权平均值;γ2为坑内开挖面以下至墙底、各土层天然重度的加权平均值;Nq、Nc为地基极限承载力的计算系数[8]。在上述计算公式中,由于岩土体本身构成复杂,各参数信息受到众多因素的影响,具有强烈的不确定性,所以可以借助盲数来描述参数的不确定性。考虑岩土体黏聚力c,内摩擦角φ为盲数,则安全系数Fs也为盲数。即(6)式可变形为:

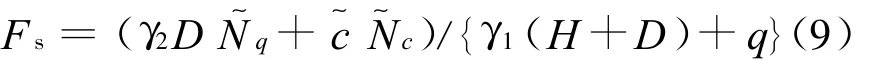
3 应 用

实例工程主楼为28层,主楼基坑开挖深度9.65 m。场地地下水位为地表下0.6～1.2 m,基坑围护结构设为2道支撑,第2层支撑到基坑地面距离为3.2 m,基坑外地面超载q=20 kPa,土的黏聚力c和内摩擦角φ取固结不排水剪指标。灌注桩长22.5 m,入土深12.85 m,工程范围内的各层土的物理力学性质指标见表1所列。

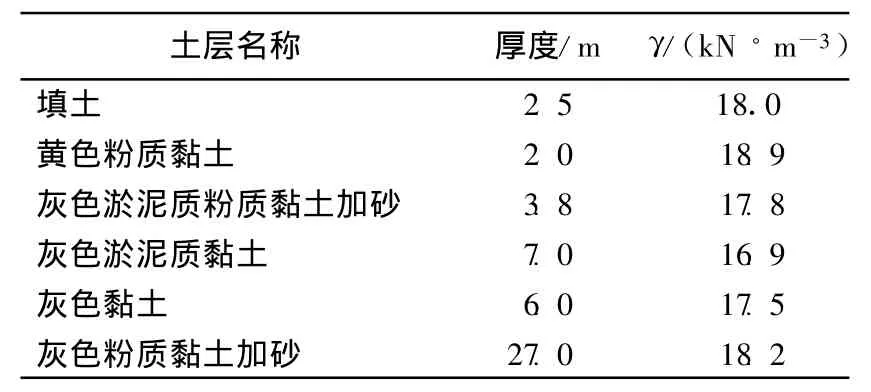
表1 各层土的物理性质指标

根据现场各参数实测资料,考虑地下水的渗流影响,在原理上属于有效应力范畴。因此土的强度指标应采用有效应力强度指标,即

可见,黏聚力在区间[3,7]内取值的可能性为0.3,在[8,12]内取值的可能性为0.7;内摩擦角在区间[6,10]内取值的可能性为0.3,在区间[11,14]内取值的可能性为0.7;其中0.3和0.7是根据实际地质情况确定的各土层在整个岩石土体内大致的分布概率。则将(10)、(11)式代入(9)式可求得相应安全系数的风险度。

在计算中要注意在盲数的四则运算中,会造成可能值矩阵区间数目的扩张。而过多地增加可能值区间的数量不仅会增加计算量,而且对于计算结果的意义不大,所以在使用(9)式计算安全系数时,要在每计算一步后将可能值区间进行适当合并,相应的可信度矩阵的数值也要随之调整,以防止解区间数目的无意义的扩张。经过计算,最后得到的安全系数的盲数表达式为:

可见,基底隆起的安全系数Fs在0.784～1.109内取值的可能性为0.12;在1.212～1.372内取值的可能性为0.18;在1.412～1.774内取值的可能性为0.45;在1.821～2.010内取值的可能性为0.25,可见安全系数在1.412以下的可能性为0.30,基坑存在一定的风险。而按传统的采用滑动体整静力平衡法,计算深基坑抗隆起稳定安全系数则为1.633。和传统方法计算的安全系数相比,安全系数的表达式比较全面地反映了在各个不同的取值区间的可能性,避免了由于参数取值单一而造成的计算安全系数时的偏差,从而能更全面地判断地基的安全稳定状态。

4 结 论

(1)由于实际基坑工程中参数具有不确定性,并且试验资料有限,本文采用盲数来描述边坡刚体极限平衡分析方法中的不确定性的计算参数,并提出计算安全系数的方法,以便充分考虑分析中所涉及的计算参数的不确定性,得到了安全系数的盲数表达形式。

(2)与以往的确定性分析方法相比,盲数可以实现将评判标准(安全系数)可能的各种情况用可信度表示,对影响因素考虑周全,从而得到更为全面的结果,给安全稳定评判提供了更加充分的依据。

(3)在运用盲数计算边坡安全系数的过程中,力学参数取位区间和条分数越多,进行运算所得的可能值区间就越多,计算量就越大。而过多、过密的取值区间对结果是毫无意义的。因此,在计算中应尽可能地根据现场的实际情况来确定参数的盲数表达形式和极限平衡计算中的条分数目,并在运算中注意区间的合并,使计算结果的表达清晰明了。

[1] 彭海铭,常为华.Rosenblueth方法在深基坑抗隆起可靠度分析的应用[J].岩土力学,2007,26(7):1132-1135.

[2] 孙淑贤.深基坑抗隆起稳定计算方法的研究[J].烟台大学学报:自然科学与工程版,1999,12(1):67-70.

[3] 孙淑贤,任凯风,张远林.基于 Terzaghi假定的基坑抗隆起稳定性计算方法研究[J].水文地质工程地质,2007,(6):64-67.

[4] 刘开第.未确知数学[M].武汉:华中理工大学出版社,1997:45-46.

[5] 刘开第.不确定性信息处理及应用[M].北京:科学出版社,1997:78-79.

[6] 李如忠,洪天求,贾志海,等.基于盲数的水体沉积物潜在生态风险评价方法[J].生态环境,2007,16(5):1346-1352.

[7] 王宏新,陈建军,刘冀山.基坑抗隆起稳定安全系数使用计算分析与应用[J].岩土力学与工程学报,2007,26(1):3223-3230.

[8] 廖 瑛.深基坑支护结构抗倾覆破坏稳定可靠性分析[J].工程勘察,2003,(6):37-40.