基于频率测试的在役简支钢箱梁桥简化安全评估

王元清, 姚 南, 张天申, 石永久

(1.清华大学 土木工程安全与耐久教育部重点试验室,北京 100084;2.清华大学 结构工程检测中心,北京 100084)

桥梁工程中常常出现发生意外事件而产生某处损伤的情况,这时便需要对损伤后的桥梁承载能力进行评估。若依照传统的桥梁评定方法,需要结合静载试验来获得评估所需的实测数据[1],但结构加载试验很繁琐。结构损伤往往使其动力特性发生变化,因此可以研究其动力参数变化(频率、振型、阻尼等)来反推结构的损伤状况。相比于振型等其它动力参数,结构自振频率具有测量便利、受污染少、精确度高等优点,因此能方便运用到实际工程检测中[2]。近年来,国内外学者研究发展了基于频率变化的损伤鉴定方法,主要有以下几类:

(1)利用频变平方比。文献[3,4]发现频率变化或不同阶频率变化比值与结构损伤位置相关,并利用有限元模型实现损伤的定位。文献[2]提出了DLAC准则,其实质也是利用不同阶频变的相对比值来实现损伤识别。

(2)采用损伤的理论模型。文献[5]利用无质量旋转弹簧模型推导了频率损伤的敏感度(矩阵);文献[6]用此模型推导了2处损伤的频率解析式;文献[2]推导了微损伤离散模型频变与损伤位置和程度的关系。

(3)利用损伤敏感度矩阵。此方法实质为矩阵反演,因其通用性以及不受损伤个数限制而得到广泛研究[7,8],国内学者也做了相关研究,如文献[9]对其进行了研究,并与神经网络方法进行了比较。

(4)利用输出误差建立最优化模型。最优化理论很早便被应用到结构参数识别中,利用频变数据建立最优化问题模型,解决损伤识别问题最具代表性的当属文献[10]的一系列研究,此外文献[11]讨论了优化函数的多种定义,并用遗传算法求解比较了不同的目标函数。

现有方法用于数值模拟和实验室模型取得很大进展,但缺乏和实际桥梁工程安全评估的联系。针对桥梁工程出现的单损伤情况,本文在前人研究的基础上推导了频变-损伤关系,并与安全评估指标相联系,提出一种在役简支钢桥简化安全评估方法。

1 离散化实用损伤评估模型

1.1 在役钢桥安全评估的前提假设

为简化问题,根据实际工程中在役钢桥安全评估的特点,本文提出如下研究假定:①钢桥具有线弹性振动行为;②承载力受刚度控制,一般钢桥若不发生开裂,承载力大多由其变形控制;③损伤对称的影响,基于频率的损伤诊断无法识别损伤对称的情况,但根据假定②,对称位置损伤对桥跨整体刚度影响是等效的,因此无需精确确定损伤位于哪个对称半区。

1.2 频变-损伤线性函数

文献[5]推导的梁结构频变比和无量纲参数K(K=KRL/(EI),KR为无质量弹簧刚度)之间的关系函数为:

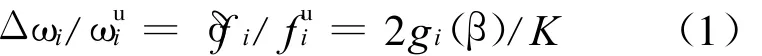
其中,下标 i表示i阶模态;上标 u表示损伤前模型;β=x/L,L为梁长(β)为损伤的位置影响函数,与该振型二阶导数的平方成正比。对有限单元又导出:

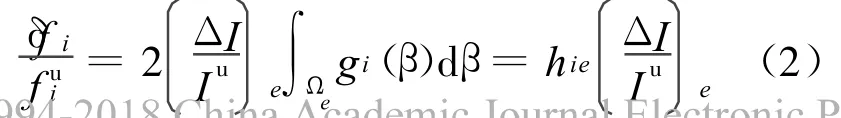
1.3 简支梁结构的离散化模型

为了方法的实用性,本文提出了一种简支梁离散化模型——区段模型(Segment Model),如图1所示,即将简支梁分为10个区段,每个区段的损伤用一等效惯性矩折减量δ Ik来表示,可定义为[5]:

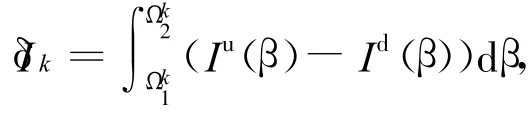
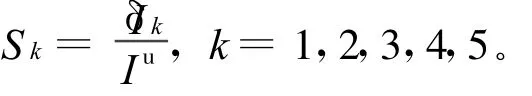
图1 区段模型

1.4 区段损伤的无量纲频变函数

易验证Fi-Sk与简支梁的几何参数无关,仅和频率阶数以及损伤位置相关。对于不同的i和k可以计算任意一根梁,便可得到基于区段模型的无量纲频变函数变化曲线。为便于工程应用,本文采取二维有限单元的方法,共计算了前5阶频率共25个结果。

对简支梁,(2)式中gi(β)表达式为[5]:

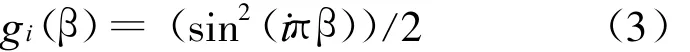
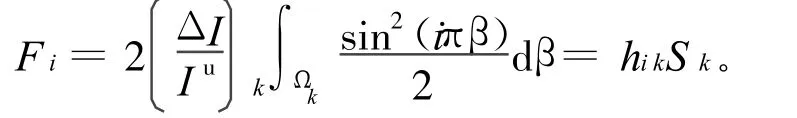
对图1中区段模型可得:

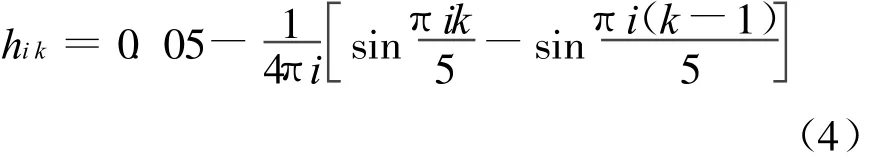
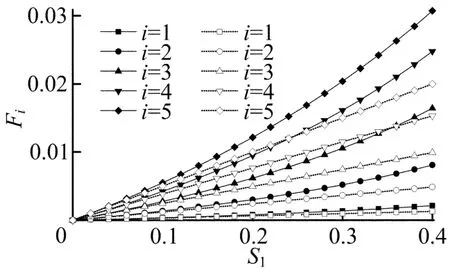
图2 k=1时2种Fi-S1关系曲线比较

由图2可知Fi-Sk关系呈弱非线性,当损伤较大时用线性关系会有较大偏差(最大约有35%)。本文采用Origin软件中的拟合工具对有限元计算结果进行了拟合,在综合考虑精度和公式实用性后最终选择二次函数Fi=aSk2+bSk进行拟合以增强方法的实用性。拟合结果见表1所列,k=5时的拟合效果如图3所示。

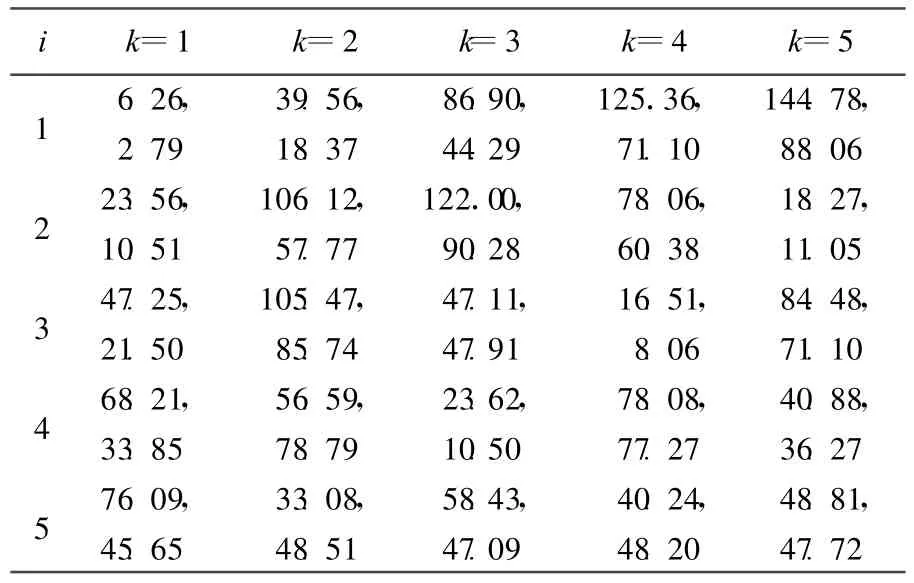
表1 a,b拟合结果 10-3

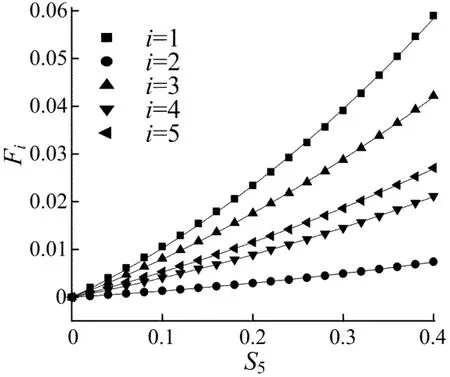
图3 k=5时拟合函数曲线

1.5 安全评估指标的推导

在现有桥梁检测规范中,关键点的位移校验系数是评价桥梁刚度最为重要的一个指标[1],定义为:η=Se/Ss。其中,Se为试验荷载作用下量测的弹性位移值;Ss为试验荷载作用下的理论计算位移值。

为了将本文的方法与桥梁的安全评定相结合,推导了简支梁在均布荷载下跨中位移校验系数的计算公式。

梁模型如图4所示,设梁在均布荷载q下的损伤前后跨中挠度分别为du和dd,由结构力学公式有:

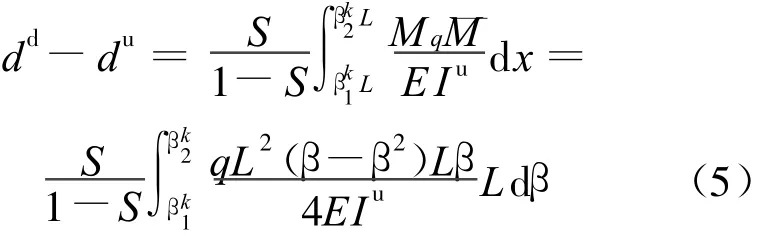
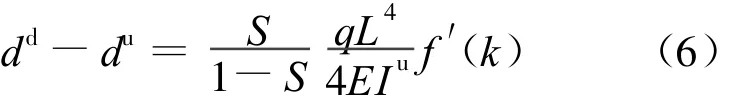
其中,f′(k)为 k的三阶函数。由材料力学公式有:

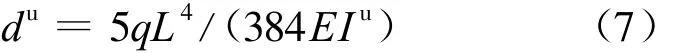
并注意到理论跨中位移校验系数:

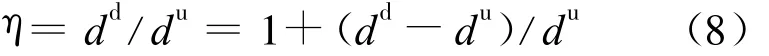
由(6)～(8)式可得:

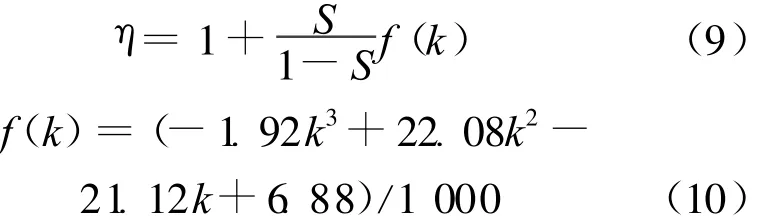
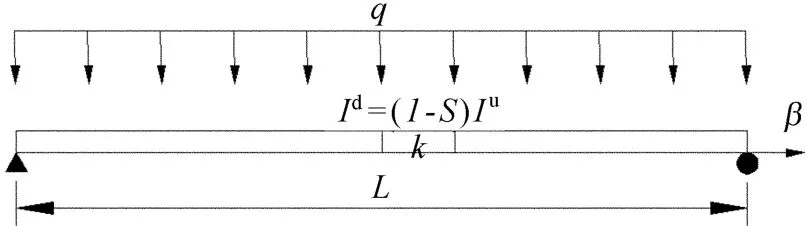
图4 损伤简支梁均布荷载模型

对于集中荷载可采用同样的方法进行推导,在此不赘述。

1.6 计算模型的初始标定

桥梁设计模型和竣工时实际状态往往存在着差异,这就需要对计算模型进行初始标定。参考文献[11]提出的标定模型,可得到如图5所示的简支梁初始标定模型。其中假定简支支座实际刚度为ks,而桥梁刚度修正系数统一设为α。实际工程中,由于桥面铺装等因素影响,一般有α＞1。

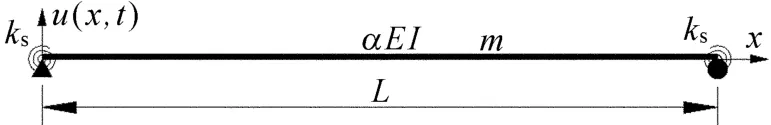
图5 简支梁初始标定模型

无阻尼欧拉梁的基本振动方程为:

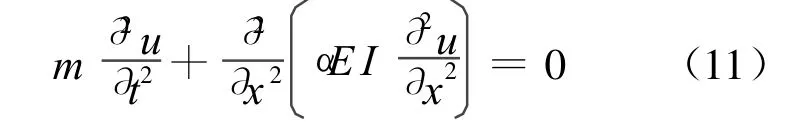
其边界条件为:

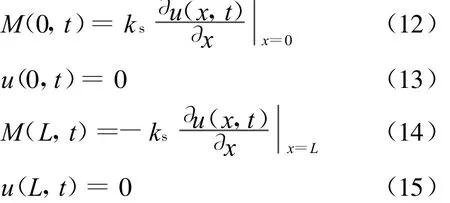
由(11)～(15)式求得角频率 ω与α以及ks之间的关系为:

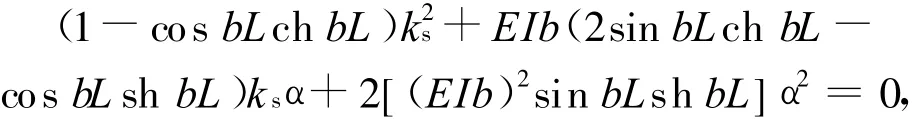
其中 ,b4=ω2m/(α EI)。

当知道竣工时桥梁的任意2阶频率,可分别代入求解二元方程组得到α和ks。方程组可用数学软件或是图解法求解,详细操作见下述算例。

得到α和ks后,用标定模型进行计算。根据结构力学中位移计算方法,(9)式修正为:

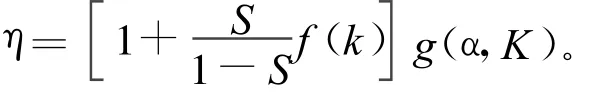
设相对刚度 K=Lks/(α EI),则有:

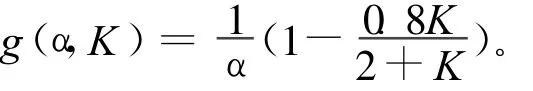
2 评估步骤与算例分析

简支钢箱梁桥的简化安全评估步骤如图6所示。

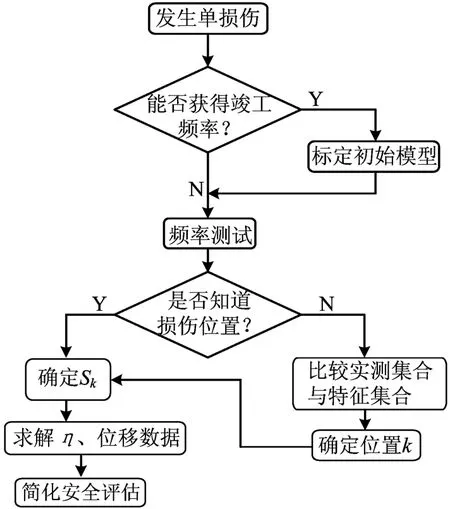
图6 简化安全评估流程

若该损伤位置未知,本文采用前人提出的不同阶频率平方的相对变化比集合来确定损伤位置[4]。对于图 1中的模型,取 S=0.3计算出集合:

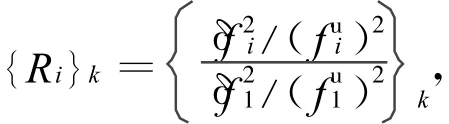
其中,i=1,2,…,5; k=1,2,…,5。

将实测集合与特征集合比较以确定损伤区段号k。具体操作见以下算例。

某简支钢箱梁桥截面如图7所示,参数如下:

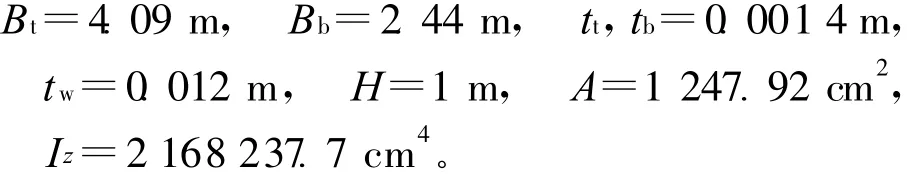
其中,t表示顶板,b表示底板,w表示腹板。

结构布置如图4所示,其中均布荷载 q=14 kN/m2,L=25 m。为验证上述方法,由简到繁设置了3种损伤工况,见表2所列。采用有限元数值模拟了3种工况下简支钢桥的前5阶竖向自振频率。

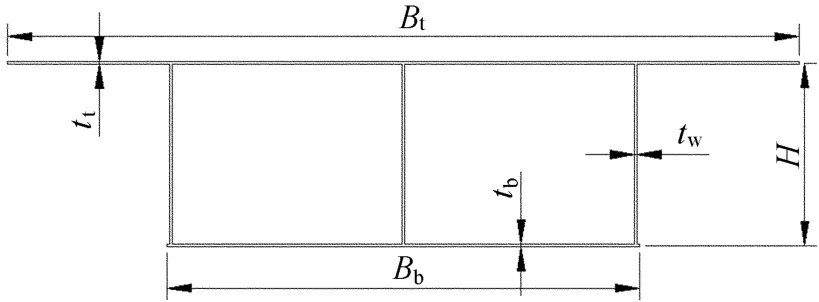
图7 钢箱梁截面

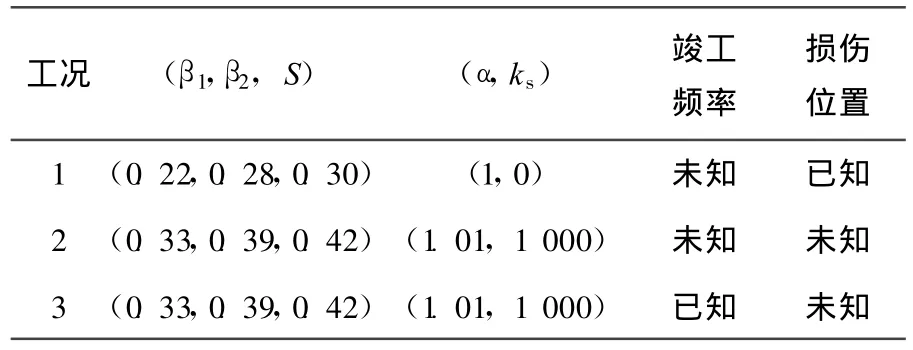
表2 损伤工况

对工况1,按照前述方法采用对损伤区域最敏感的前3阶频变计算,并取平均值得到S和η的推定值,见表3所列,可以看到和理论值的误差只有0.02%,推定结果较为理想。

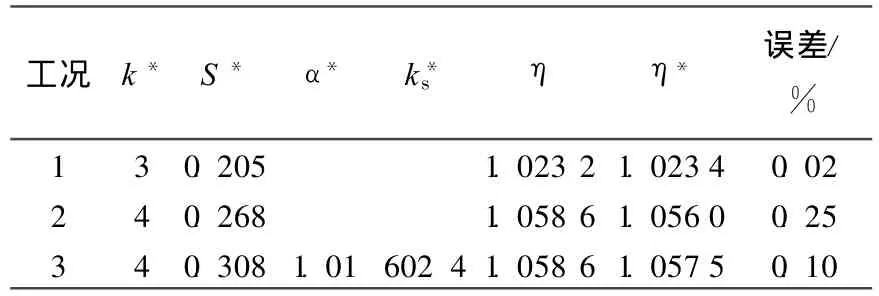
表3 计算结果

特征{Ri}k集合示于图8中,对工况2和工况3,从图8中可以看出,实测集合(用虚线表示)与k=4特征集合接近。测试{Ri}k与特征{Ri}k均方差列于表4中,可以看出k=4时值最小,因此对该损伤位置识别正确。

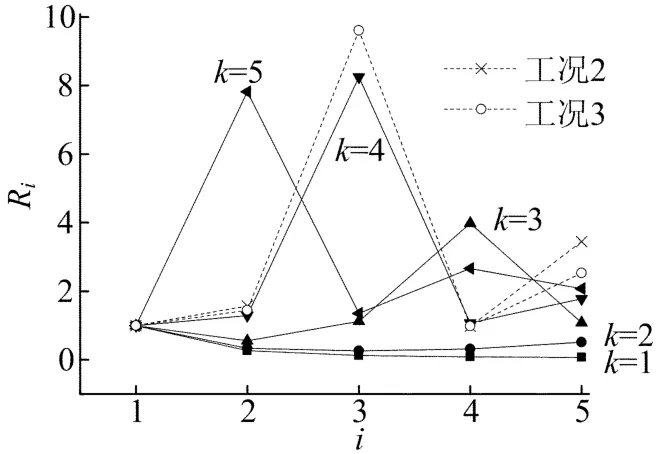
图8 特征{Ri}k集合(k=1～5)

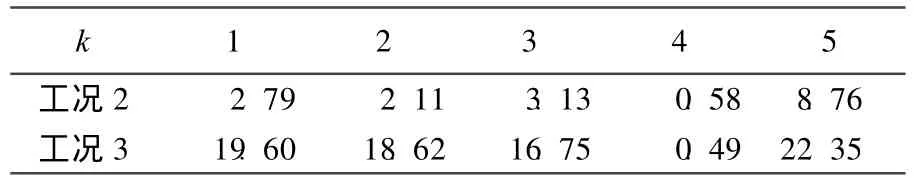
表4 测试{Ri}与特征{Ri}k均方差

以同样方法得到工况2和工况3的η推断值以及误差(见表3)。α与ks的推定如图9所示。可以发现,同样的损伤状态,工况3进行初始标定(图9)后得到的η推断值更准确,误差由0.25%降到0.10%,因此计算模型的初始标定能提高此方法桥梁安全评估的精度。

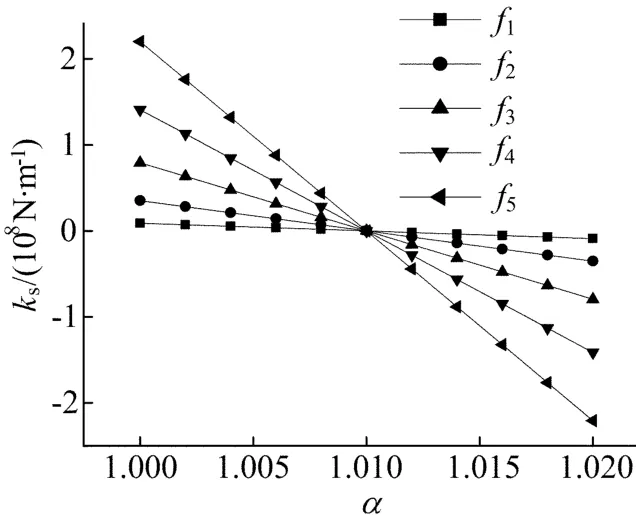
图9 α与ks的推定

3 结 论

(1)对于简支梁局部损伤,与以振型不变为假设前提的线性关系相比,采用非线性的频变-损伤关系在大幅度损伤时(超过20%)更为准确。

(2)对初始计算模型的标定影响到最终安全评估的精度,因此利用本文方法对简支钢桥进行简化安全评估时,竣工(损伤前)频率数据的获得是很有必要的。

(3)本文将拟合的简支梁非线性Fi-Sk关系与桥梁检测评估指标η相联系,得出一种单损伤时简支钢箱梁桥的简化评估方法,并用数值模拟验证其有效性,但此方法仍需要实际工程或相关试验的进一步验证。

[1] 刘自明,王邦楣.桥梁工程检测手册[M].北京:人民交通出版社,2002:125-128.

[2] Messina A,Williams E J,Conturis T.Structural damage detection by a sensitivity and statistical-based method[J].Journal of Sound and Vibration,1998,216(5):791-808.

[3] Cawley P,Adams R D.The location of defects in structures from measurements of the natural frequencies[J].Journal of Strain Analysis,1979,14(2):49-57.

[4] Hearn G,Testa R B.Modal analysis for damage detection in structures[J].Journal of Structure Engineering,1991,117(11):3042-3063.

[5] Liang R Y,Hu J,Choy F.Quantitative NDE technique for assessing damages in beam structures[J].Journal of Engineering Mechanics,1992,118(7):1468-1487.

[6] Morassi A,Rollo M.Identification of two cracks in a simply supported beam from minimal frequency measurements[J].Journal of Vibration and Control,2001,7(5):729-739.

[7] Patil D P,Maiti S K.Experimental verification of a method of detection of multiple cracks in beams based on frequency measurements[J].Journal of Sound and Vibration,2005,281:439-451.

[8] Xu G Y,Zhu W D,Emo ry B H.Experimental and numerical investigation of structural damage detection using changes in natural frequencies[J].T ransaction of the ASM E,2007,129:686-700.

[9] Zhu Hongping,He Bo,Chen Xiaoqiang.Detection of structural damage through changes in frequency[J].Wuhan University Journal of Natural Science,2005,10(6):1069-1073.

[10] Vestroni F,Capecchi D.Damage evaluation in cracked vibrating beams using experimental frequencies and finite element models[J].Journal of Sound and Vibration,1996,2(1):69-86.

[11] Ruotolo R,Surace C.Damage assessment of multiple cracked beams:numerical results and ex perimental validation[J].Journal of Sound and Vibration,1997,206(4):567-588.