基于改进遗传算法的混合装配生产线平衡问题研究

扈 静, 蒋增强, 葛茂根, 杜伟山

(合肥工业大学机械与汽车工程学院,安徽合肥 230009)

装配线的平衡性是生产型企业所追求的重要目标之一,指的是各个装配程序以及工位上生产任务的排列如何保证每个工序或者工位要求的装配时间接近于不变,并且具有相同或者近似相等的总作业时间。即在对生产线进行划分时,力图使每个工序或工位的作业进程同步输入与输出,使生产线上每个工位上的物件流动处在同一生产速度上,而不会出现工件等待加工的物流阻塞现象。

近年来,文献[1-5]对一条装配线进行单产品装配及混合多产品装配进行了研究,但这些研究多数是基于1个工位只装配1个产品的数学模型,而在实际的装配生产过程中,1个工位装配的产品也许不止1个,有可能是2个或者多个产品同时在1个工位上装配。例如某车桥厂汽车主减装配线,1个工位可以同时装配3个同类型(或不同类型)产品。针对1个工位多个产品装配的模型中,只考虑1个产品装配或者简单地将产品合并叠加计算,显然不能满足装配生产线的平衡要求。本文以1个单工位装配多种主减的混合装配生产线模型为例对其平衡性进行研究,设计了一种基于激素调节机制的改进遗传算法对其进行仿真分析,以验证模型的可行性、有效性。

1 单工位多工件的混合装配生产线

单工位多工件混合装配生产线是指在装配生产线的任意一个工位上,都有多个同种类型(或者不同类型)的产品在进行装配。

由于一个工位装配多个产品需要考虑每个产品的装配顺序约束关系,还要综合考虑产品的装配时间、相关属性以及产品的混合装配比,即不同种类产品装配线上的投放比例,因此,装配线平衡研究具有一定的复杂性、多变性与不确定性。

2 激素调节机制

内分泌系统是生理信息传递系统,通过分泌多种激素来调节机体的生理功能,维持内环境的相对稳定。内分泌细胞将其产生的激素,随血液和细胞间液传送到机体的各部位,对所作用的细胞的生理活动起着兴奋性或抑制性作用,生物内分泌系统在维持机体内环境的稳定方面起着不可替代的作用[6]。

人工内分泌系统(AES)是指在研究人体内分泌系统的信息处理机制的基础上,构造出体现内分泌系统的信息处理特性的一类新的人工智能模型和方法。

文献[7]曾提出了对激素腺体分泌激素的通用规律,激素的变化规律具有单调性和非负性,激素分泌调节的上升和下降遵循Hill函数规律,如(1)式 、(2)式:

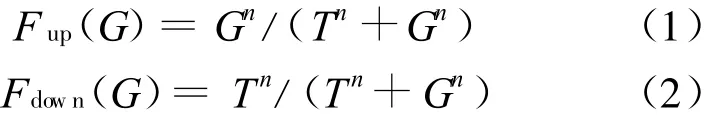
其中,G是函数自变量;T为阀值,且 T＞0;n为Hill系数,且n≥1,n和T共同决定曲线上升和下降的斜率。该函数具有如下性质:

3 基于激素调节机制遗传算法

3.1 适应度函数的构造

一条平衡性好的装配生产线,不仅要求装配生产线工位间的负荷均衡,还要考虑减少成本和装配生产线上的工位数,可以节约生产线占地面积、减少物料搬运设备和相关的夹具设备,从而降低企业的制造成本。这里引入平衡损耗系数d:

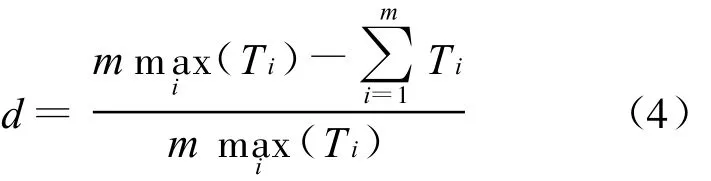
其中,max(Ti)表示瓶颈工位加工时间,即所有工位时间最长;m为总工位数;d表示由于生产线上工位之间作业分配不均而导致的空程时间比率,d值越大表示工位损失时间越多。

在平衡的装配生产线上,要求装配生产线上各个工位间的负荷均衡,由生产线的平滑指数SI来表示,SI越小表示生产线工位的负荷越平衡,即

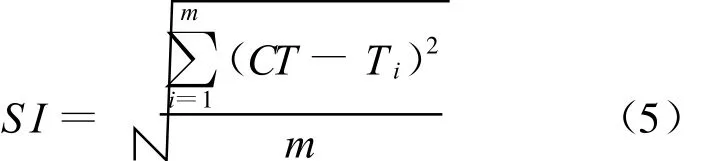
其中,CT为生产节拍;Ti为每个工位的加工时间;m含义同前。

综合考虑生产线平衡损耗状况和平衡状况,构造目标函数如下:

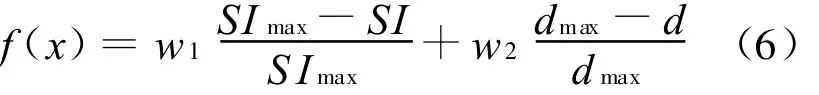
其中,w1和 w2为权重系数;SImax、dmax分别为每代粒子中SI、d的最大值。函数的第1部分保证装配生产线的平衡,第2部分保证装配生产线上的工位数最少,一般取 w1+w2=1。w1和w2的取值根据目标函数对装配生产线平衡和工位数的要求而定,若w1＞w2,则表示使生产线负荷平衡的目标比工位数目最少的目标更重要。所以最终的算法适应度函数为:

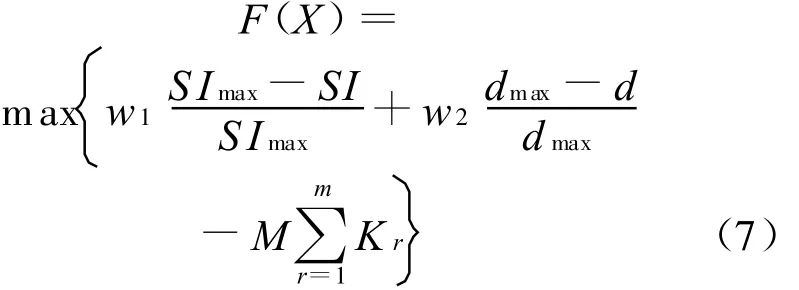
3.2 编码和解码

为了便于描述模型的实际意义,减少计算量,现采取遗传算法的实数编码方式。

1个染色体由所有工序排列组成,代表1种生产线平衡方案的可行解。例如,一生产线上的产品由A1,A2,A3,A4,A5,A66道工序组成。加工时间分别为 2.2 s、1.1 s、1.4 s、2.0 s、1.6 s、1.5 s,如果基因表示1个可行解,那么根据对染色体的解码过程,就可以得到染色体适应度值的大小,并可以划分出工作站中工序,求出一个生产线平衡率。

根据上述的编码方式,问题的编码是按照作业要素的优先顺序来进行的,解码时按照编码的顺序依次计算作业要素的累积时间T,并与生产线节拍CT进行比较,当计算到第i位编码时累积时间Ti仍小于CT,再向下累加到第i+1位编码时,若Ti+1大于CT,则以前面i个编码对应的作业要素分配给第1个工位,依次进行直到把对应编码中所有的作业要素分配完毕。以图1所示的编码进行解码,假设生产线节拍为3 s,得到图2所示的解码。

图1 问题编码示例

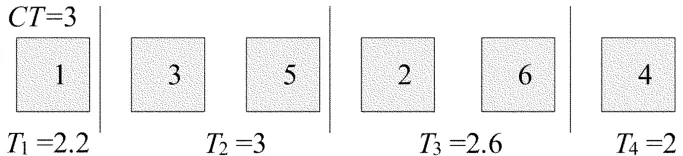
图2 问题解码示例

3.3 初始种群的生成

为了提高算法运算效率及计算结果的精度,本文在初始生成染色体时使染色体为可行解,并在优化计算过程中始终保持染色体为可行解,以避免染色体在算法运算过程中变为不可行解。

初始染色体种群的生成采取无前趋的顶点优先的拓扑排序方法,即对每个节点进行遍历,以出度数、入度数表示紧前工序、紧后工序的工艺约束,该方法的每一步总是输出当前无前趋(即入度为零)的顶点。

3.4 选择算子

遗传算法在选择复制时,根据适应度确定每个个体选择复制为下代个体数量,即

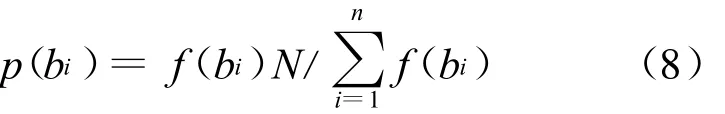
其中,N为群体中的总个体数量;f(bi)为个体的适应度;bi表示第i个个体。可见,适应度越高,作为父代个体的次数越多;反之亦然。

3.5 交叉算子

交叉是遗传算法中的重要步骤,交叉算子将被选中的2个个体的基因链按一定概率pc进行交叉,从而生成2个新的个体,在传统遗传算法中pc是常量,而在本文的改进遗传算法中,pc根据激素调节机制设置[8],如(9)式:

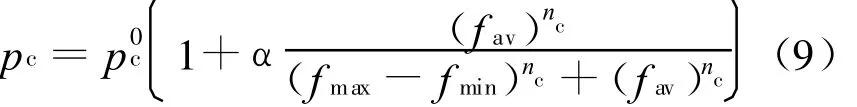
3.6 变异算子

同样在变异过程中,实时检验新产生个体的适应度。如果适应度低于父代个体,则新个体被删除并以原个体替代。为了加快收敛速度或增加个体多样性,同样按照激素调节规律,自适应变异因子如(10)式:

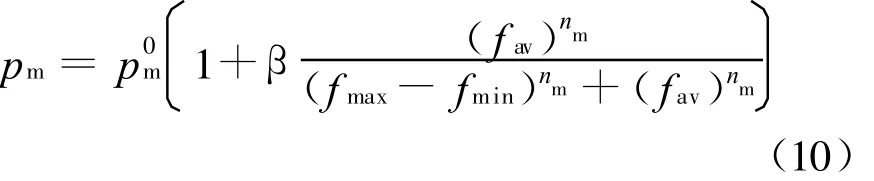
4 中后桥主减混合装配线工位平衡仿真

本装配线上,同时生产型号不同的后桥和中桥主减2种产品,在某时间段内中桥主减的需求量为100台,设为 A产品,后桥主减的需求量为200台,设为B产品。

假设一天的生产时间为8 h,480 min,产量为120台/d,其生产节拍CT=4 min,其在生产装配线上投放比例为后桥∶中桥=2∶1。由于后桥和中桥是相互独立的工件,它们之间没有工艺顺序约束,根据表1、表2的后桥、中桥主减工艺流程表装配顺序约束的优先关系,可以得到它们的混合优先关系,如图3所示。

遗传算法参数取初始染色体数为500,采用到达指定代数来终止迭代的循环方式,循环迭代次数取200代,即算法运算200代后终止,取交叉率=0.6,变异率=0.2,α=0.2,β=0.1,nc=nm=2,w1取0.6,w2取0.4,M=10 000,使用Matlab编写基于激素调节机制遗传算法程序,并将模型中的中桥、后桥各工序装配时间及工艺装配约束关系数据代入仿真程序,得到的结果如图4所示。

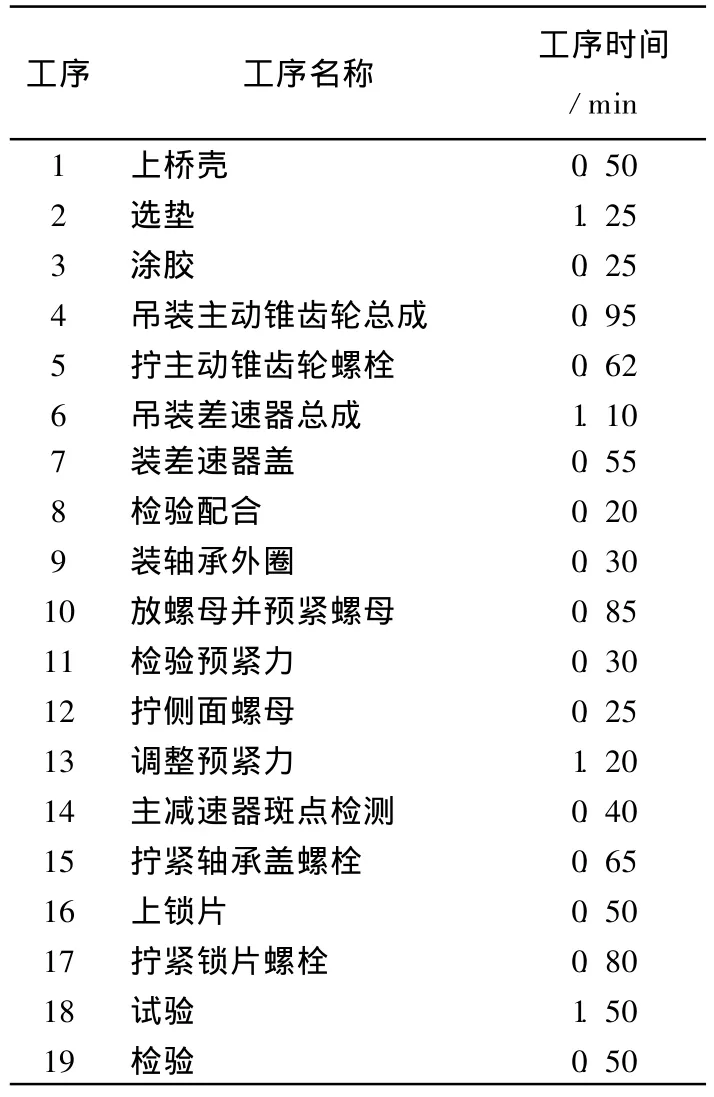
表1 后桥主减总成工艺流程

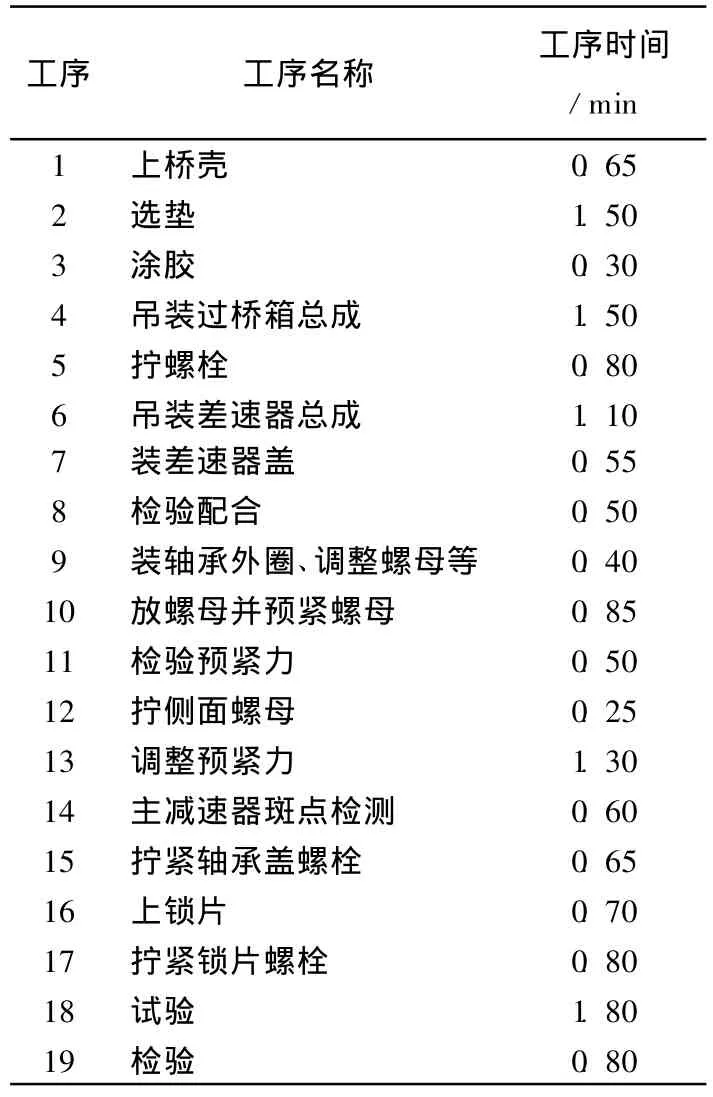
表2 中桥主减总成工艺流程

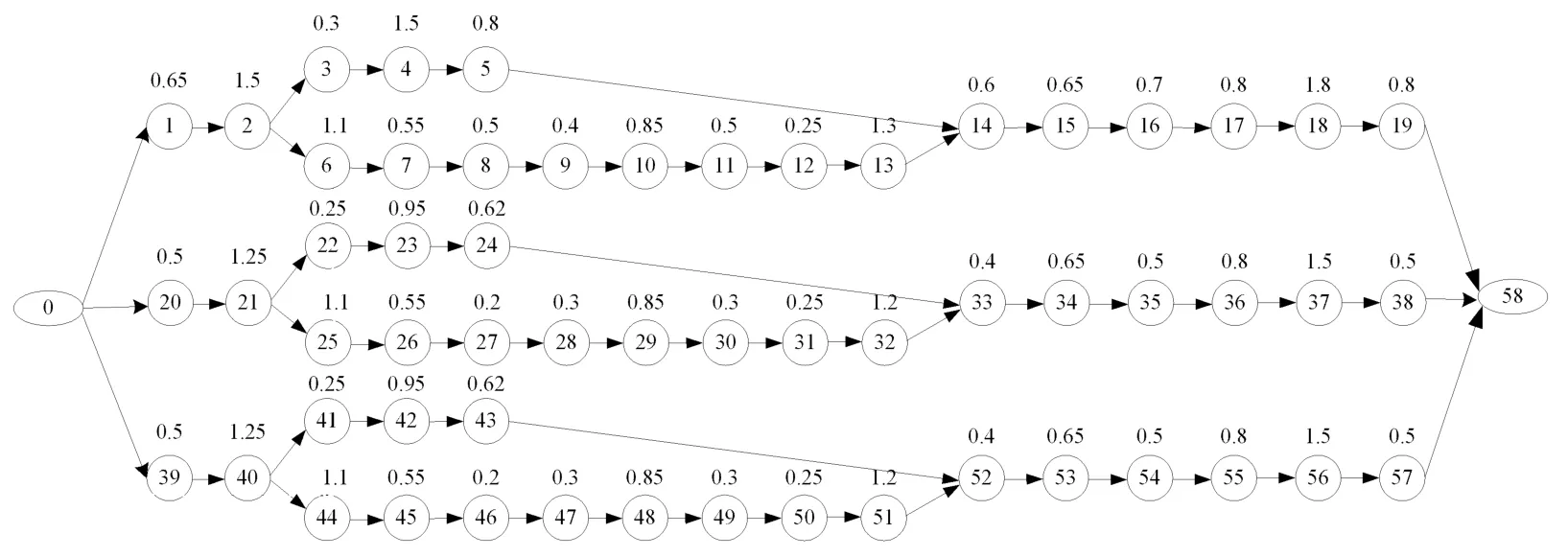
图3 混合优先关系图

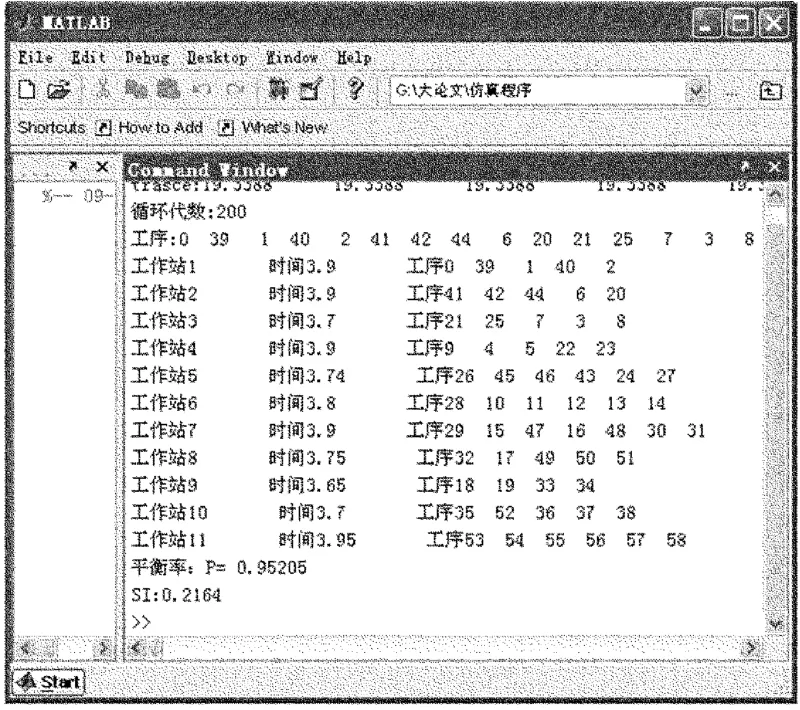
图4 仿真结果

图5所示为激素调节机制的遗传算法收敛曲线,由图中可以看出,经过少量迭代次数后,算法迅速收敛于最优值。

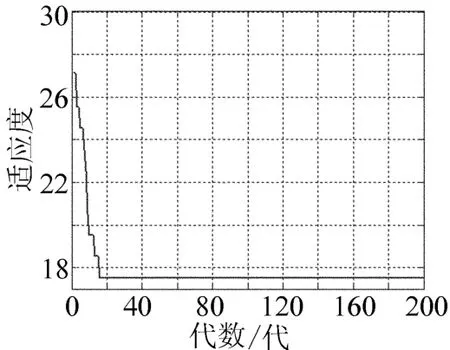
图5 收敛曲线图

由图4的仿真结果可知,最终得到的工位数量为11个,平滑性指数SI=0.216 4,计算生产线平衡率P=0.952 05。结果表明,采用该模型可以极大地提高装配生产线整个生产阶段的平衡性,从而降低订单的总加工时间。

5 结束语

本文采用基于激素调节机制的改进遗传算法对混合装配生产线平衡问题进行了研究,并对单工位多工件装配线模型的平衡性进行了分析。通过对单工位多工件的汽车中、后主减混合装配线工位平衡仿真,在一定程度上验证了该模型与算法可以提高生产线平衡性的可行性与有效性。

[1] Sabuncuoglu E E,Tanyer M.Assembly line balancing using genetic algo rithms[J].Journal of Intelligent Manufacturing,2000,11(20):295-310.

[2] Jackson J R.A computing procedure fo r a line balancing problem[J].Management Science,1956,(2):261-271.

[3] Haq A N,Rengaranjan K,Jayaprakash J.A hybrid genetic alg orithm approach to mixed-model assembly line balancing[J].International Journal of Advanced Manufacturing Technolgoy,2006,28(3):337-341.

[4] Bard J F,Shtub A,Joshi S B.Sequencing mixed-model assembly lines to level parts usage and minimize line length[J].International Journal of Production Research,1994,(34):2431-2454.

[5] Leu Y,Matheson L A,Rees L P.Assembly line balancing using genetic algo rithms[J].Decision Science,1994,25(4):581-606.

[6] 谢启文.现代神经内分泌学[M].上海:上海医科大学出版社,1999:56-58.

[7] Farhy L S.Modeling of oscillations in endocrine networks with feedback[J].M ethodsin Enzymology, 2004,384:54-81.

[8] 王 祎,陈为栋,顾幸生,等.基于内分泌调节免疫算法的Flow shop调度问题[J].系统仿真学报,2008,13(20):3425-3430.