考虑参数空间变异性的不排水边坡可靠度分析

潘健，周森

（华南理工大学土木与交通学院，广东广州510640）

考虑参数空间变异性的不排水边坡可靠度分析

潘健，周森

（华南理工大学土木与交通学院，广东广州510640）

采用验算点法和随机有限元法对不排水边坡进行可靠度分析，研究边坡坡度、安全系数和强度参数相关性对边坡可靠度的影响.数值分析结果表明，由于随机有限元法恰当地考虑了土性参数的空间变异性，因而当土体抗剪强度参数变异系数超过临界值时，边坡失效概率计算结果更为合理.

边坡稳定；不排水边坡；有限元法；失效概率

0 引言

岩土工程问题的不确定性使得可靠度分析方法在岩土工程领域受到广泛关注.可靠度分析方法最早是由Wu和Craft[1]引入到边坡稳定性分析中的，Alonso[2]、Tang等[3]以及Vanmarcke[4]等对早期边坡可靠度分析方法的应用做出了较大贡献.随后，国内外专家学者[5-9]对这种分析法进行了较为系统的研究，推动了可靠度分析方法在边坡工程中的应用和发展.

目前，边坡可靠度分析中最常用的方法是验算点法、概率距点估计法、响应面法、MC模拟法，而随机有限元方法的应用则相对较少.常规边坡可靠度分析不同程度地存在着简化与假设较多、未考虑变量的空间变异性及概率分布等问题，从而也限制了其工程应用；随机有限元法却可以较好地模拟土性参数的空间变异性，得到较为合理的结果.鉴于此，本文以随机有限元法（RFEM）[10]为分析手段，以不排水边坡为对象，研究坡度、安全系数和强度参数空间相关距离及变异系数对边坡可靠度的影响，并与验算点法（FORM）的结果进行对比.

1 强度参数概率分析

为研究土性参数变异性对边坡可靠度的影响，取简单边坡剖面如图1所示.坡高H=10.0 m，坡底深度为20 m，土体容重γsat（或γ）=20.0 kN/m3.对于不排水边坡，把抗剪强度指标cu（φu=0）看做一随机变量，无量纲化为Cu=cu（γsatH）.考虑坡角α为18.4°（坡度3∶1）、26.6°（坡度2∶1）和45°（坡度1∶1）等3种不同情况.

假设抗剪强度参数Cu服从对数正态分布.虽然可供选择的相关函数有多种，但对数正态分布方法简单，不需要迭代计算，可由古典正态（高斯）分布经过简单的非线性变换构造得到，还可以确保随机变量总为正值.基于对数正态分布的这种优势，目前很多学者都提倡用这种方法对土体性质进行模拟，对随机变量Cu的具体描述可参考文献[11].

对数正态分布下的抗剪强度Cu对应3个参数：均值μCu，标准差σCu和空间相关距离θlnCu.Cu的变异性可由变量的无量纲系数表示为:

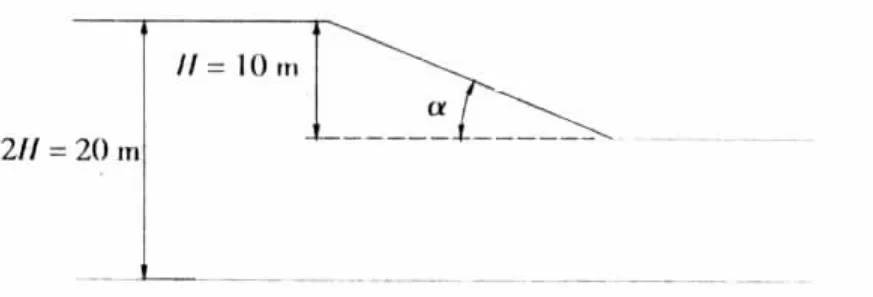
图1 简单边坡剖面图

Cu对数的标准差和均值可以由Cu的标准差和均值表示如下：

由公式（1）、（2）和（3）反算出Cu的均值和标准差为：

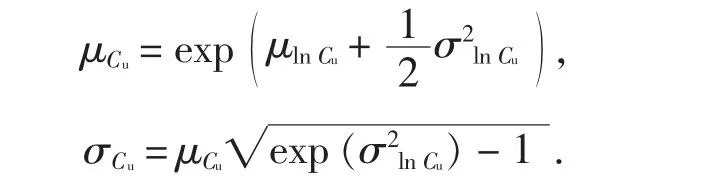
因为实际的不排水抗剪强度场服从对数正态分布，故抗剪强度参数Cu的对数服从隐式正态分布（高斯）场.空间相关距离的确定与这个隐式场有关，也即与抗剪强度参数Cu的对数lnCu有关.特别地，空间相关距离有特定的范围（指相关函数为指数或高斯函数时，函数值衰减到e-1时的距离，e为自然对数底），一旦超过这个特定范围，空间随机值在隐式高斯场则呈现显著相关性.所以，较大的空间距离与平缓变化场对应，而较小的空间距离对应场的变化却呈现波动性.

在本文中，取指数衰减相关函数形式为：

ρ（τ）指由绝对距离τ离散的随机场中两点土性参数间的相关系数.在现行研究中，通常将空间相关距离除以边坡坡高H，使其无量纲化为：

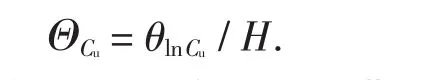
不同空间相关距离对应的典型破坏机制如图2所示.

图2 空间相关距离对土坡可靠度的影响

图2（a）、（b）分别表明了ΘCu=0.2和2时空间距离对土性参数相关性的影响，较小的波动范围值意味着土性变化较大，较大的波动范围值意味着土性变化较平稳.图中明、暗网格单元分别代表低强度和高强度土体区，黑色代表土体强度最高的单元，白色代表土体强度最低的单元.需要强调的是，这两种情况下抗剪强度分布分析基于相同的对数正态分布，仅仅空间相关距离有所不同.

由离散点试样得到的土体抗剪强度参数的均值、标准差和空间相关距离等特性只能反映“点”特性[12].虽然按照这种方法获取的参数特性并不能完全反映实际工程问题，但它们代表着土体内在的变异性，这种变异性可通过考虑样本容量的局部平均法来调整.在用随机有限元法（RFEM）进行分析时，每一个有限单元网格都具有常量属性，用来离散边坡的每一个有限单元网格的大小就代表了样本容量.如果点分布服从正态分布，那么由局部平均法得到的方差减小，均值不受影响；而在对数正态分布中，由局部平均法得到的均值和标准差都会减小.运用局部平均法对代表对数正态场的均值和标准差进行调整，并把调整后的均值μCuA和σCuA标准差映射到有限单元网格上.取极限，当ΘCu→0时，局部平均剔除了所有偏差（σCuA→0），均值趋近于算术平均值，故：

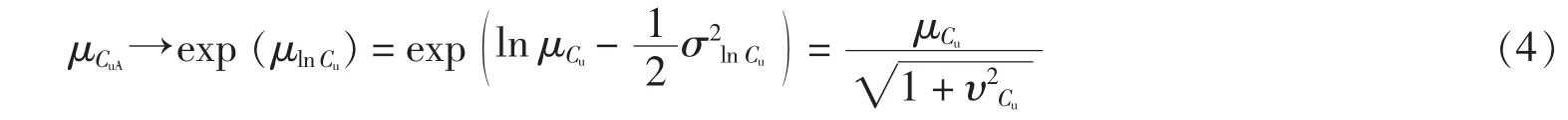
2 验算点法（FORM）

2.1 边坡算例

常规的验算点法（FORM）[13]没有考虑空间相关距离对边坡可靠度的影响，即认为空间相关距离ΘCu=∞，此时局部平均法已不再适用.对于不排水边坡，在本文中，选取服从对数正态分布的随机变量Cu作为边坡可靠度分析参数.失效概率pf可简单等同于抗剪强度参数Cu不超过Cu，Ks=1时的概率，其中Ks表示安全系数，Cu，Ks=1代表安全系数为1时对应的Cu值.在数量关系上，失效概率pf等同于对应Cu≤Cu，Ks=1时，概率密度函数与坐标轴所围成的面积.例如，当坡角α=26.6°（坡度2∶1）时，对应Cu，Ks=1=0.17.假定μCu=0.25，σCu=0.125（υCu=0.5），代入公式（2）、（3）得到隐式正态分布的均值和标准差分别为μlnCu=－1.489，σlnCu=0.472.失效概率计算如下：

其中，Φ·为标准正态分布概率分布函数.

为研究安全系数Ks对边坡可靠度影响，对于μCu=Cu，Ks=1.25=0.21，μCu=Cu，Ks=1.47=0.25和μCu=Cu，Ks=1.70=0.29时，不同υCu对应的失效概率如表1所示.为达到参数研究目的，找到υCu对应的临界值，在一些情况下，取υCu值高达1.5.

考虑坡度的影响，研究中发现对于不排水边坡，无论在哪种情况下，只要安全系数相同，坡度对失效概率的影响就没有差别.因此，表1所示的失效概率值对任何坡度都适用.

2.2 FORM和Hasofer-Lind可靠度指标

运用验算点法（FORM）可以计算涉及多元随机变量系统的失效概率，多元随机变量概率密度函数与极限状态函数对应，极限状态函数能将失效区和安全区划分开来.传统的FORM基于Hasofer-Lind[13]可靠度指标βHL， 认为随机变量的均值位于极限状态函数的安全区，可靠度指标在几何上表示为标准化正态空间中均值和极限状态面之间的最短距离，其计算涉及到迭代优化过程.根据当量正态化后的随机变量（即验算点）位于极限状态面上，由此可以从中找到使可靠度指标达到最小值时对应的相关矩阵.一旦确定了可靠度指标，那么就可以定义失效概率如下：

表1 不同变异系数υCu的失效概率

需要注意的是，当失效概率大于50%时，可靠度指标为负值[14].对于二维随机变量，由一阶假设得到的极限状态函数表示一条直线，失效概率表示位于极限状态线失效区一侧由二元概率密度函数和坐标平面所围成的体积值.对于涉及多元随机变量的情况，采用类似的计算方法.

每一种可靠度分析方法都需要确定一个极限状态函数，以对安全或失效状态进行界定.极限状态分为承载力的极限状态和正常使用的极限状态.通常极限状态方程表示如下：

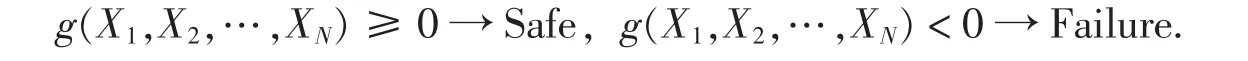
其中，X1，X2，…，XN为随机变量.表示相关正态变量的Hasofer-Lind指标βHL和表示相关非正态变量的FORM指标β的优势在于，可靠度指标与极限状态函数的具体形式无关，是极限状态函数的不变量.极限状态函数可以定义为抗力减去荷载、安全系数减1、安全系数的对数或者其它不影响可靠度指标计算值的代数组合.

具体来说，FORM是通过迭代过程来确定可靠度指标的.为显式地考虑变量之间的相关性，可靠度等效计算公式为[15]：

其中，Xi为第个i随机变量，为第i个随机变量的等效正态化均值，为第i个随机变量的等效正态化标准差，{（Xi-）/}为随机变量标准正态化矢量，R为相关矩阵.

3 随机有限元法（RFEM）

3.1 RFEM特性

本节运用弹塑性有限元模型，结合蒙特卡罗数值模拟的RFEM[11]进行分析，并与FORM结果进行对比.RFEM需要生成随机场特性并将其映现到有限单元网格上，对分布类型并没有严格的限制，随机场是在隐式正态空间中生成的，可以很容易地将正态分布映射到其他类型的分布中.在每个单元网格上，充分考虑局部平均和方差折减，并建立指数衰减的空间相关函数.随机场初始生成后，赋予每个单元网格土体特性，并将重力荷载加于有限单元网格上.运用蒙特卡罗模拟进行多次重复计算，每一次蒙特卡罗分析过程都是在相同的均值、标准差和土性空间相关距离条件下进行的，但是土性参数的空间分布却各不相同.根据足够数量的分析循环次数，失效概率可以很容易地由失效次数和总模拟次数的比值来确定，分析过程也包含了土体特性和各向异性空间相关距离的互相关性.

典型单元网格由图2所示.图2共划分了910个有限单元，因此对不排水边坡共包含910个随机变量.大多数情况通常模拟2 000次，对较大空间相关距离（Θ≥1.0）和变异系数（υ≥1.0），通常模拟5 000次.本文的目的就是要找到变异系数临界值υcrit及其对应下的失效概率值.若要求失效概率的最大误差为10%，可靠度为90%，那么要计算模拟的次数为2 435次，因此模拟2 000次基本能够达到最终的误差界限.

3.2 边坡算例

取υCu为定值μCu=Cu，Ks=1.47，υCu为0.1，0.2，…，1.0，为，…，2，4.由RFEM分析所得3种不同坡度边坡失效概率与FORM所得结果（Θ＝∞时）比较如图3所示.

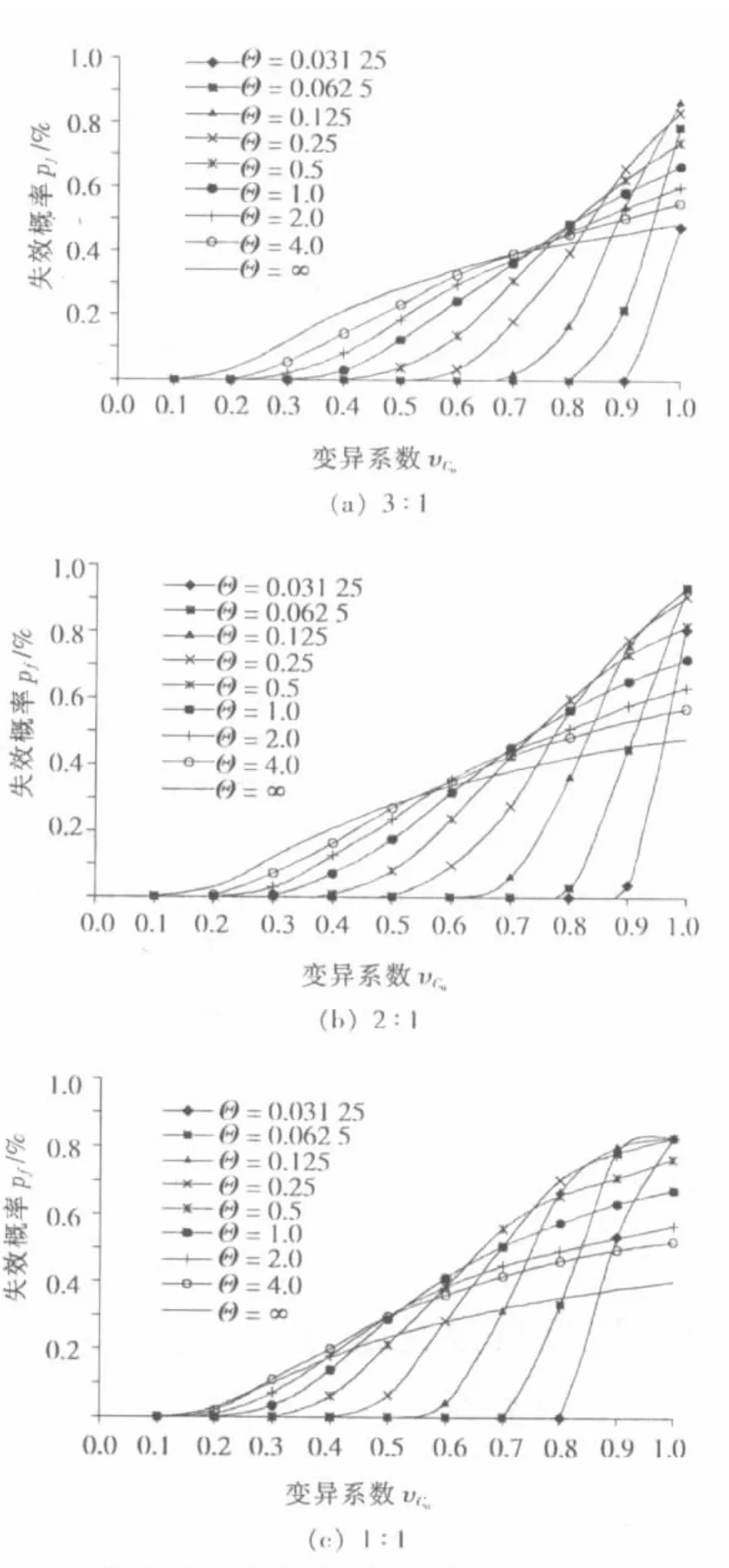
图3 3种边坡所得失效概率（Ks=1.47）

对于FORM，忽略空间变异性，在相同Ks下对应不同坡度的边坡，其坡度大小对失效概率并无影响.但运用RFEM，坡度较大的边坡对应的失效概率比坡度较小时对应的失效概率大.造成这一现象的原因在于RFEM的计算程序可以通过破坏机理在各向异性土体中自动找出最危险破坏路径.对于较为平缓的不排水边坡，破坏路径通常位于土体深部并且通过坡底土体；对于较为陡峭的边坡，破坏路径却有多种，或许会穿过坡趾，或许会通过坡底土体，因此具有较高的破坏概率.

为研究Ks对边坡的影响，采用以上类似的计算方法.对于2∶1边坡，取和μCu=，结果见图5.表明忽略空间变异性使得Ks较高的边坡在较低υcrit值下的失效概率偏低，而Ks较低的边坡则对应更低的υcrit值.

图4 Ks=1.47时不同坡度的ΘCu-υcrit关系

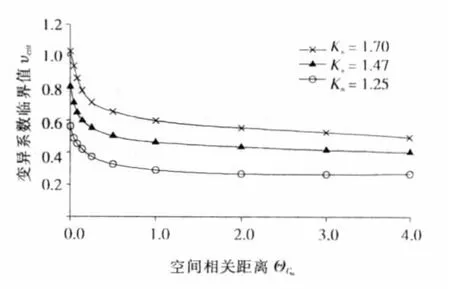
图5 不同Ks值的ΘCu-υcrit关系

4 结语

1）本文采用验算点法（FORM）考虑土性参数空间变异性，并结合蒙特卡罗数值模拟的随机有限元法（RFEM），对不排水边坡失效概率进行了分析.与忽略参数空间变异性的方法（FORM）相比，RFEM能够根据破坏机理在各向异性土体中找到最薄弱应力路径，因此计算所得失效概率更高.

2）数值分析结果表明，当抗剪强度参数变异系数超过临界值υcrit，忽略参数空间变异性使得边坡失效概率偏于不安全；υcrit值越低，忽略空间变异性造成对失效概率估计偏低的可能性越大.

3）通过相关图表得到了υcrit大小与不同参数组合间的关系：i）与具有高安全系数的边坡相比，低安全系数的边坡对应更低的υcrit；ii）对不排水边坡，坡度较大的边坡比坡度小的边坡具有更低的υcrit.

[1] Wu T H，Craft L M.Safety analysis of slopes[J].Journal of Soil Mechenics and Foundation，Eng Div，ASCE，1970（96）：609-630.

[2] Alonso E E.Risk analysis of slopes and its application to slopes in Canadian sensitive clays[J].Geotechnique，1976（26）：453-472.

[3] Tang W H，Yucemen M S，Ang A H S.Probability based short-term design of slopes[J].CanadianGeotechnical Journal，1976（13）：201-215.

[4] Vanmarcke E H.Reliability of earth slopes [J].Journal of Geotechnical Engineering，ASCE，1977，103（11）：1 247-1 265.

[6] 高大钊.岩土工程设计安全度指标及其应用[J].工程勘察，1996（1）：1-6.

[7] 罗文强，黄润秋，张倬元.斜坡稳定性概率分析的理论与应用[M].武汉：中国地质大学出版社，2003.

[8] 包承钢.可靠度分析方法在岩土工程中的应用[J].人民长江，1996，27（5）：1-5.

[9] Christian J T，Ladd C C，Baecher G B.Reliability applied to slope stability analysis[J].Journal of Geotechnical Engineering，ASCE，1994，120（12）：2 180-2 207.

[10] Griffiths D V，Fenton G A.Probabilistic slope stability analysis by finite elements[J].Journal of Geotechnical and Geoenvironmental Engineering，2004，130（5）：507-518.

[11] Fenton G A，Griffiths D V.Risk assessment in geotechnical engineering[M].Canada：John Wiley&Sons Ltd，2008.

[12] 吴振君.土体参数空间变异性模拟和土坡可靠度分析方法应用研究[D].武汉：中国科学院武汉岩土力学研究所，2009：6.

[13] 吴世伟.结构可靠度分析[M].北京：人民交通出版社，1990.

[14] Low B K.Reliability-based design applied to retaining walls[J].Geotechnique，2005，55（1）：63-75.

[15] Low B K，Tang W H.Reliability analysis using object-oriented constrained optimization[J].Structural Safety，2004，26（1）：69-89.

Analysis of Influence of Spatial Variability on Undrained Slope Reliability

PAN Jian，ZHOU Sen
(College of Civil Engineering&Transportation，South China University of Technology，Guangzhou 510640，Guangdong，China)

The first-order reliability method and the random finite-element method were used to study the probability of failure of undrained slopes.The influences of slope inclination，factor of safety and cross correlation between strength parameters on a criticalvaluewereinvestigatedbyparametricstudies.Numericalresultsshowthat random finite-element method in which spatial variability of soil properties is properly accounted for can result in reasonable estimates of the probability of failure if the coefficient of variation of the shear strength parameters exceeds a critical value，which may provide a reference for design of undrained slope.

slope stability；undrained slope；finite element method；probability；failures

TU 432

A

1001-4217（2010）03-0074-07

2010-03-01

潘健（1963-），男，广东广州人，博士，副教授.研究方向：岩土工程地下结构设计方法和风险评估.E-mail：cvpan@scut.edu.cn