基于四维混沌系统的数字图像加密

叶瑞松，陈永洪

（汕头大学数学系，广东汕头515063）

基于四维混沌系统的数字图像加密

叶瑞松，陈永洪

（汕头大学数学系，广东汕头515063）

提出基于四维混沌系统的数字图像加密算法.利用四维混沌系统产生的伪随机序列，对数字图像像素值的二进制分块进行空间位置置乱.实验结果表明，该算法密钥空间大，具有好的置乱度，加密效果好，安全性高，可以有效防止统计攻击，并具有抗剪切、加噪等攻击的能力.

四维混沌系统；置乱；加密

0 引言

现代科技日新月异，数字图像成为信息的重要载体.现代高性能计算机每秒可搜索数百万个底码，未加密的图像存在安全威胁，传统图像加密算法正面临极大压力[1-2]，混沌系统具有初始值极端敏感依赖性、轨道遍历性等性质，为信息加密算法提供了更多的选择[1-3].已有文献提出基于混沌系统的加密算法有：基于Arnold变换、Baker变换、Logistic映射以及基于混沌系统生成二进制序列的方法等[1-6].对于低维混沌的加密方案，已经有一些攻击方法可以将其破解[7-8].高维混沌系统有更好的随机性和初始值敏感性，基于高维混沌系统的加密算法可以获得更好的加密效果.本文利用Qi等[4]提出的四维混沌系统生成4个混沌序列，选取序列中元素的小数部分，使之分布在区间（0，1）上.与传统的单纯改变像素空间位置相比，本文提出的算法可以同时改变像素值和像素位置，较少置乱次数就可以达到较好的置乱效果.像素值空间位置置乱后引入像素值扩散算法，能获得更好的安全性能.数值实验表明，本文提出的加密算法有足够大的密钥空间，可以抵抗统计攻击和差分攻击，并有抗剪切、涂鸦污染、加噪攻击的能力.

1 四维混沌系统

Qi等[4]提出自治四维混沌系统：其中X=[x1，x2，x3，x4]T是状态变量，a，b，c，d是正值参数.当a=35，b=10，c=1，d=10，取初始值X0=[1，1，1，1]T，系统（1）有混沌吸引子如图1所示.

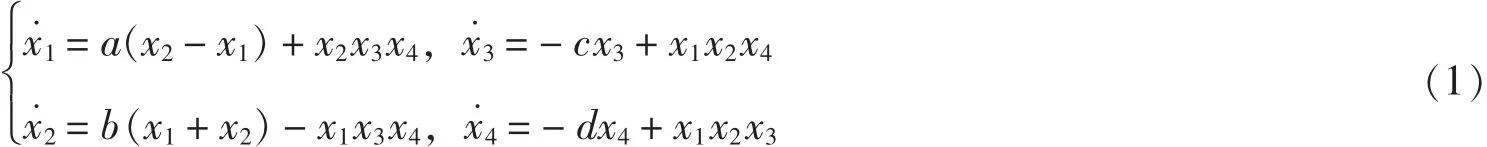
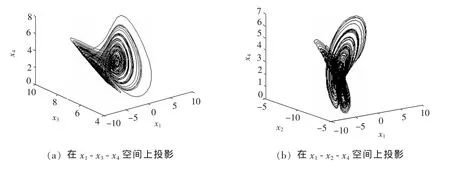
图1 四维混沌吸引子在三维空间上的投影

2 基于四维混沌系统的加密算法

与文献［6］中基于混沌系统生成二进制序列加密算法不同，本算法通过量化混沌轨道序列，利用混沌轨道的遍历性置乱图像.

2.1 混沌序列的生成

运用Runge-Kutta方法求解混沌系统（1），取a=35，b=10，c=1，d=10，步长h=0.005，初始值为X0=[1，1，1，1]T，生成4个离散混沌系列为X1，X2，X3，X4，其中Xi=为使生成的序列是分布在[0，1]上的伪随机序列，对混沌系列作如下处理：

2.2 基于像素值二进制分块的空间位置置乱

i）如图2，假设图像数据大小为M×N二维矩阵I，将数字图像像素值转化为二进制，从而将二维矩阵I扩展构成三维矩阵′（以大小256×256的Lena灰度图像为例）.

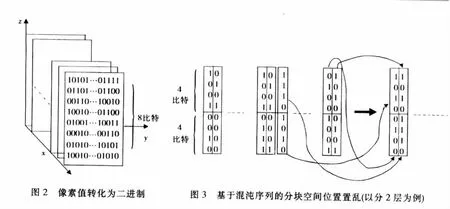
iv）由x（i），y（i），z（i）完成全部随机选取次数后，按索引矩阵J中元素值是否为0判断A中未选取到的元素，即若J（j）=0，令B（k）=A（j），k=k+1，此时k的值由步骤iii）中k的值确定.

v）将I″转化为十进制并存储为二维矩阵，完成一次置乱，重复ii），iii），iv）步骤可完成多次置乱，提高置乱度.

2.3 像素值的扩散

虽然通过上述基于像素值二进制分块空间位置置乱达到了改变原图像像素值的目的，但为防止统计和差方攻击，有必要对置乱后图像像素值进一步扩散.

扩散算法如下.

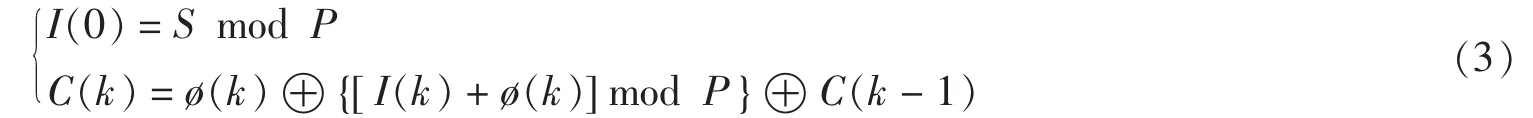
式中，S是扩散过程初值密钥，为正整数，I（k）是原图像像素值空间位置置乱后输出的第k个像素值，C（k）为扩散后的像素值，P为图像灰度级位数，“⊕”为按位异或运算.其逆扩散过程函数为：

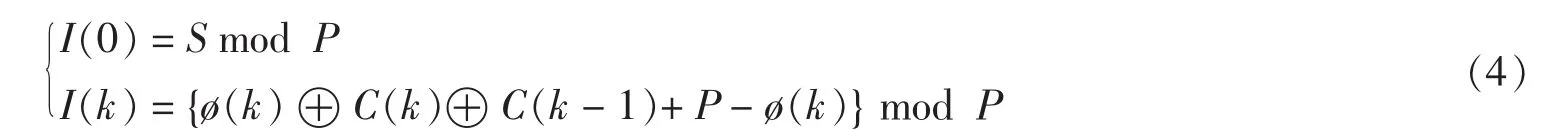
上述加密算法可逆，加密图像的解密过程即为上述加密算法的逆算法.

2.4 加密实验

以大小为256×256 Lena灰度图像为例，混沌系统（1）中a=35，b=10，c=1，d=10，取初始值X0=[1，1，1，1]T，三维二进制块分为上下层，置乱次数为3进行实验，加密效果如图4所示.

从图4可以看出，图（b）空间位置置乱3次已达到较好的效果.本文加密算法具有较大周期，可通过增加置乱次数提高置乱度，但同时对计算机计算速度提出更高的要求.

3 加密安全性能分析

一个好的加密算法不仅需要较好的加密效果，同时必须具有足够大的密钥空间，能较好地防止明文攻击、统计、差分等攻击，并具有抗剪切、涂鸦污染、噪声污染等鲁棒性.下面对本文算法的安全性能进行分析.

3.1 密钥敏感性分析和密钥空间

加密算法必须具有对初始值的极端敏感性和足够大的密钥空间，以抵抗穷举法等非法攻击.

密钥敏感性测试对大小为256×256的Lena图像进行加密实验，取两组不同初始值分别为：

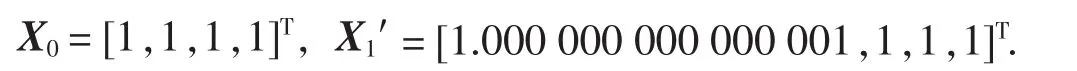
四维混沌系统（1）中，a=35，b=10，c=1，d=10，分为2层，加密次数为3次.两者加密图如图5所示.

从图5（e）可以看出，虽然初始值X0，X0′只相差10-15，但用初始值X0′无法正确解密

图5（b），同时，可以比较分别用初始值X0，′得到的不同加密图（b）与（c）.用以下方法比较图5中（b）与（c）不同的程度：

其中D，D′是分别用不同初始值加密得到的加密图，n表示D，D′像素值不同的点个数，C表示D，D′对应位置像素值不同点的比例.数值计算表明，图5中（b）与（c）不同的程度：C=98.516 8%，图5（d）是表明（b）与（c）的差别图像.以上实验表明本算法对初始值很敏感.

密钥空间加密算法的初始密钥包括四维混沌系统包含的4个参数a，b，c，d，初始值X0，扩散过程中扩散初始值S，分层数K以及置乱次数T.由上面密钥敏感性测试知，初始值最小差别可以达到10-15，而扩散初始值S可以在0～255选取，所以，不包括4个混沌初始参数的密钥空间至少为P×8×1031×1031×1031×1031＝8P×10124，P为图像灰度级.同时加密过程还必须确定三维二进制如何分层，由于分层与图像灰度级P有关，这进一步扩大了本文算法的密钥空间，增加了破解难度.由此可见本文加密算法可以具有足够大的密钥空间.

3.2 统计分析

攻击者可以通过统计加密图中像素值相关性进行攻击解密，所以，如何有效地去除加密图像像素值相关性，实现加密图像像素值的有效扩散，是衡量加密算法有效性的途径之一.本文算法在空间置乱过程中实现像素值二进制分块移动后，利用按位异或运算有效地改变原图的像素值相关性.如图6所示，图（a）原图直方图分布不均，图（b）置乱后改变了原图的直方图，但仍分布不均，图（c）加密图直方图分布均匀.

为进一步比较原图和加密图像素相关性的差别，分别从原图和加密图中随机选取1 000个相邻（垂直、水平、对角）的像素，计算相关系数，实验结果如表1所示.图7给出了原图和加密图垂直方向相邻像素的相关性，可以看出，原图垂直方

表1 原图与加密图相邻像素相关系数比较

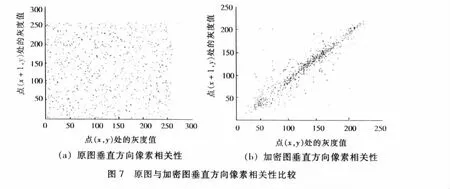
向像素相关性强，而加密图垂直方向像素相关性弱.

攻击者可以通过改变原图一个像素值大小，判断加密图数目改变率，进行差分攻击或明文攻击.为抵抗差分攻击或明文攻击，要求上述改变率越大越好.用NPCR和UACI衡量本算法抵抗差分攻击的有效性.NPCR是指当原图一个像素改变时加密图像素数目改变率，改变率越大表明加密算法对原图越敏感，越能抵抗明文攻击；UACI是指原图和加密图的相应像素平均强度的变化率，变化率越大，表明加密图与原图比平均强度变化越大，加密算法越好，越能抵抗差分攻击.NPCR与UACI定义[5]如下：

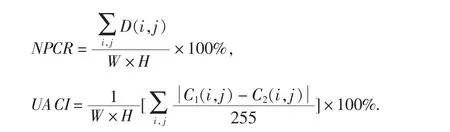
其中C1，C2分别为只有一个像素值不同的两个原图的加密图，D（i，j）的定义为：若C1（i，j）≠C2（i，j），则D（i，j）＝1，否则D（i，j）＝0；W，H为C1，C2的宽和高.

以Lena原图为例，改变（8，8）处像素值为160做加密实验并分析NPCR和UACI的值，其值情况如表2所示，可以看出当加密次数为1时效果就相当良好.

表2 NPCR和UACI测试结果

3.3 攻击实验

为了检验本文加密算法的鲁棒性，对大小为的256×256的Lena灰度图像加密3次后的加密图进行剪切、涂鸦污染、加噪等攻击.实验结果如图8所示，表明本算法有较好的鲁棒性.

图8 剪切、涂鸦污染、加噪攻击及解密效果图

4 结语

本文研究了基于四维混沌系统的图像加密算法.利用像素值二进制表示法，将二维图像像素值矩阵扩展为二进制的三维矩阵，并通过对像素值二进制分块和扰乱达到置乱图像像素位置空间目的，且对置乱后的图像像素值扩散，去除了原图像像素值相关性，可以有效抵抗统计分析和差分攻击.数值实验表明，本算法可以达到很好的加密效果，具有足够大的密钥空间，符合加密算法的要求.攻击实验也表明算法具有抵抗剪切、涂鸦污染、加噪等攻击的鲁棒性.

[1] 李昌刚，韩正之，张浩然.图像加密技术综述[J].计算机研究与发展，2002，39（10）：1 317-1 324.

[2] Shannon C.Communication theory of secrecy systems[J].Bell Syst Tech J，1949（28）：656-715.

[3] Xiang Tao，Liao Xiaofeng，Tang Guoping，et al.A novel block cryptosystem based on iterating a chaotic map[J].Physics Letters A，2006（349）：109-115.

[4] Qi Guoyuan，Chen Guanrong.Analysis and circuit implementation of a new 4D chaotic system[J].Physics Letters A，2006（352）：386-397.

[5] Chen Guanrong，Mao Yaobin，Chui C K.A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos Solitons and Fractals，2004（21）：749-761.

[6] 程东升，叶瑞松.基于四维混沌系统生成二进制序列的方法及其加密应用[J].计算机应用，2008，28（3）：875-878.

[7] Wang Shihong，Kuang Jinyu，Li Jinghua，et al.Chaos based communications in a large community[J].Phys Rev，2002，66（6）：1-4.

[8] 倪皖荪,华一满.混沌通讯[J].物理学进展,1996，16（3，4）：645-655.

Digital Image Encryption Based on a 4D Chaotic System

YE Rui-song，CHEN Yong-hong
(Department of Mathematics,Shantou University,Shantou 515063,Guangdong,China)

A novel image encryption scheme based on a 4D chaotic system is proposed.The plaintext binary block is permuted by pseudo random number generated by a 4D chaotic system.The proposed scheme has big key space and improves the scrambling degree.Simulation results show the high security and good encryption effect of the new scheme.The statistical analysis shows that it provides an efficient and secure way against statistical attack.The proposed scheme is robust against cropping and noising attacks as well.

4D chaotic system；scrambling；encryption

TP 391

A

1001-4217（2010）03-0058-08

2009-09-21

叶瑞松（1968-），男，福建漳州人，教授.研究方向：分歧理论及其数值计算，分形混沌及其计算机应用.E-mail：rsye@stu.edu.cn