利用海洋强迫的大气主模态提高大气动力季节预报
2010-10-20林海
林海
(加拿大国家环境预报中心气象研究部,加拿大魁北克多尔瓦勒 H9P1J3)
利用海洋强迫的大气主模态提高大气动力季节预报
林海
(加拿大国家环境预报中心气象研究部,加拿大魁北克多尔瓦勒 H9P1J3)
数值模式的季节预报技巧主要与大气外强迫的变率密切相关。当前的大气环流模式(general circulation models,GCMs)通常不能准确地模拟出与大气外强迫有关的响应模态和响应强度,从而导致了预报误差的产生。本文给出了一种后处理方法,有助于降低模式的系统性误差,并提高季节预报技巧。
动力季节预报;海洋强迫模态;数值模式
0 引言
大气的年际变率不仅可以由大气内部机制产生,还可以由大气的外强迫过程产生。在动力季节预报中,人们一直在寻找来自大气外部的变化缓慢的外强迫产生的信号。而与大气内部动力过程有关的那部分年际变率则被认为是不可预测的气候噪声。因此,季节预报的任务就是识别出这种有用的信号,而忽略掉气候噪声。这通常是通过利用耦合的大气—海洋模式或者大气环流模式来实现。在利用大气环流模式时,变化缓慢的海表温度(sea surface temperature,SST)是已知的。与大气相比,海表温度具有更长时间尺度的可预报性。为了捕捉这种外强迫产生的信号,通常采用集合预报技术。在集合预报中,在要进行预报的季节,人们利用大气环流模式进行一组数值积分试验。这些数值积分应用相同的海温边界条件,但是具有不同的初始条件。成员足够多的集合预报试验的平均结果则反映了与边界强迫有关的信号。
决定预报技巧的另一个重要因素是大气环流模式对边界强迫的响应是否如同实际大气一样,即:数值模式能否就实际大气对外强迫的响应在强度和空间分布上进行逼真的模拟。由于模式在构建和参数化方案等方面总是会有缺陷,所以所有的数值模式均会存在误差。因此模式大气对边界强迫(例如:海表温度异常)的响应通常存在偏差并依赖于模式本身的性能。此外,除了改善和提高模式性能外,人们也致力于发展大气环流模式积分的后处理方法来减少模式误差[1-4]。
为了订正大气对热带海温异常的响应模态,基于模式预报的外强迫产生的信号的SVD(singular value decomposition,奇异值分解)主模态和历史观测资料的回归,本文提出了一种统计方法。该方法被应用于冬季500 hPa位势高度场[5]以及加拿大降水[6]的预测,其预报技巧得到显著提高。该方法也被应用于加拿大气温(surface air temperature,SAT)的季节预报的订正[7],结果表明,在原始的预报技巧非常低的秋季,气温的预报技巧能够得到明显提高。
1 模式和资料
本文分析了HFP第二阶段(the second phase of the Historical Forecasting Project,HFP2)的集合预报试验的输出结果。HFP2是一项由加拿大的一些大学和政府实验室承担的一项协作项目。该项目的目的是检验能够在多大的程度上达到季节平均状态的潜在可预报性。Derome等[8]报道了HFP在第一阶段(the first phase of HFP,HFP1)的试验设置,并给出了一些试验结果。在HFP2,利用4个大气环流模式进行了季节集合预报的历史回报试验。这4个大气环流模式分别是,加拿大气候模拟和分析中心(the Canadian Centre for Cl imateModelling and Analysis,CCCma)的第二、第三代大气环流模式(GCM2和GCM3),以及RPN(Rechercheen prévision numérique)的降分辨率版本的全球谱模式(SEF)以及RPN的全球环境多尺度模式(Global Environmental Multiscale model,GEM)。
在以前的研究中,GCM2被用来进行气候数值模拟[9-10]。GCM2是一个全球谱模式,水平分辨率为T32,垂直方向分为10层。GCM3拥有GCM2的许多基本特征,但是其分辨率有明显提高,水平分辨率为T63,垂直方向分为32层,而且它的许多参数化物理过程得到改进。在过去的研究中,SEF被用于全球资料同化和中期天气预报[11-12]。它也是一个全球谱模式,水平分辨率为T63,垂直方向分为23层。GEM是加拿大气象中心(the Canadian Meteorological Centre)的业务应用模式[13-14]。在HFP2,GEM模式采用了2°×2°的水平分辨率,垂直方向分为50层。
集合预报试验时间是1969—2003年,模式积分从每个月的开始时间运行,每个模式做10次积分,积分长度是4个月。大气初始条件取自模式预报时段之前的NCEP/NCAR再分析资料[15],10个积分试验的时间间隔为12 h。全球海表温度用的是预报时段前1个月的持续的海温异常,即:将预报时段前1个月的海表温度异常加到预报时段的气候平均场中。在积分的前15 d里,通过向气候场逼近的方法对海冰进行初始化。海温和海冰资料均来自于S M IP-2(the Seasonal Prediction Model Intercomparison Project-2)边界资料[16]。应用NCEP逐周观测资料,雪盖也得到了初始化处理[17]。
采用NCEP/NCAR提供的500 hPa位势高度场再分析资料,计算了太平洋—北美型(the Pacific-North American pattern,PNA)指数和北大西洋涛动(North Atlantic Oscillation,NAO)指数。PNA和NAO是北半球冬季主要的大尺度低频大气模态[18]。用于分析和比较的逐月降水资料由英国东安格利亚大学(University of East Anglia)气候研究中心(Climate Research Unit,CRU)提供。
本文仅分析始于12月1日的冬季观测资料和模式预报结果。由于CRU降水资料终止于2002年,所以共分析了1969/1970—2001/2002年的33个冬季情况。相对于夏季而言,冬季的季节平均降水更多地受到大尺度环流的控制;而在夏季,局地对流更加重要,因而预报也更加困难。此外,冬季的中纬度对流层的强西风带为Rossby波的向北传播提供了有利条件,因此,热带影响可以传到高纬度地区。PNA和NAO在冬季比夏季更强。
2 对热带太平洋海表温度异常的响应模态
本文分析了集合试验的两个3个月时段(12月—次年2月代表了预报的1~3个月,1—3月代表了预报的2~4个月)的平均北半球500 hPa位势高度场。对于每个大气环流模式,采用奇异值分解方法[19]分析了集合试验的3个月的平均高度场与之前11月的热带印度洋—太平洋(120°E~90°W,20°S~20°N)海表温度之间的协方差(据前所述,在12月—次年3月的预报中用的海表温度是之前11月的持续的SST异常)。SVD主模态的大气环流场反映了与热带印度洋—太平洋SST结构有关的主要的强迫模态。为了与观测资料进行比较,对观测的500 hPa位势高度场和前面相同的海温场进行了相似的SVD计算。结果代表的是观测的位势高度场与热带SST异常之间的一种滞后的联系。
由1—3月观测资料分析的SVD模态见图1。由图可见,在位势高度场上,SVD1和SVD2分别与PNA、NAO具有相似的分布特征。SVD1和SVD2解释的协方差平方分别为61%和12%。SVD1大气分量的主成分(APC1)与观测的PNA指数的相关系数为0.96,而SVD2大气分量的主成分(APC2)与观测的NAO指数的相关系数为0.94。这里,观测的1—3月PNA和NAO指数是通过将观测的1—3月500 hPa位势高度场到投影到冬季逐月500hPa位势高度场的第一和第二旋转EO F模态上得到。
SVD1的SST分量的空间分布反映了典型的ENSO信号。因此,当前期11月热带东太平洋的SST为正异常时,大气中1—3月的PNA型也为正位相。SVD2的SST分量的空间分布可能不常见,它表现为沿赤道太平洋的负SST异常特征,其中心位于热带中西太平洋。SVD分析表明,11月的这种SST分布导致了大气中1—3月正位相的NAO。12月—次年2月的SVD结果与1—3月的SVD结果非常相似。
如果季节预报是有技巧的,那么上述观测资料中大气与海温间的联系应该能够被大气环流模式模拟出来。图2为GEM集合预报结果的第一和第二对SVD模态。由SVD1(图2a)可见,在太平洋和北美地区,预报的PNA型与观测结果非常相似。然而,SVD2的大气分量与观测的NAO型相去甚远(图2b)。对其他三个模式的集合预报做SVD分析也得到类似的结果。这四个模式的SVD的前两个SST分量的分布在热带地区具有很多相似性(图2c和2d)。但是,它们的大气响应对模式具有相当的依赖性,四个模式的结果不尽相同(图略)。
尽管大气响应模态的空间分布对模式具有依赖性,但是它们相应的时间变化(APC1和APC2)分别与观测的PNA指数、NAO指数呈显著的相关关系,12月—次年2月和1—3月的情况如表1所示。由表1可知,APC1和APC2与PNA和NAO的相关均通过了0.05信度的显著性检验。这表明,PNA和NAO的信号在集合预报中可以得到较好的模拟。用大气环流模式模拟结果的前两个主成分(APC1和APC2)来代表PNA指数和NAO指数,具有显著的预报技巧。L in等[5]研究认为,一种利用了模式预报的SVD主模态时间系数的订正方法,可以有效地提高PNA和NAO的预报技巧。

图1 观测的1—3月500 hPa高度场(a,b)与前期11月海温场(c,d)的SVD1(a,c)和SVD2(b,d)模态(各模态的强度相当于时间系数的1个标准差;(a)、(b)、(c)、(d)中等值线间隔分别为10 m、10 m、0.3℃、0.1℃;(c)和(d)中阴影区分别表示大于0.6℃、小于-0.1℃的SST异常)Fig.1 Observed(a,b)JFM 500 hPa height and(c,d)previous November SST distributions of(a,c)SVD1 and(b,d)SVD2(The magnitude corresponds to one standard deviation of each time coefficient.The contour interval is 10 m for(a)and(b),0.3℃for(c),and 0.1℃for(d).The shaded areas in(c)represent SST anomaly values greater than 0.6℃,whereas those in(d)smaller than-0.1℃)
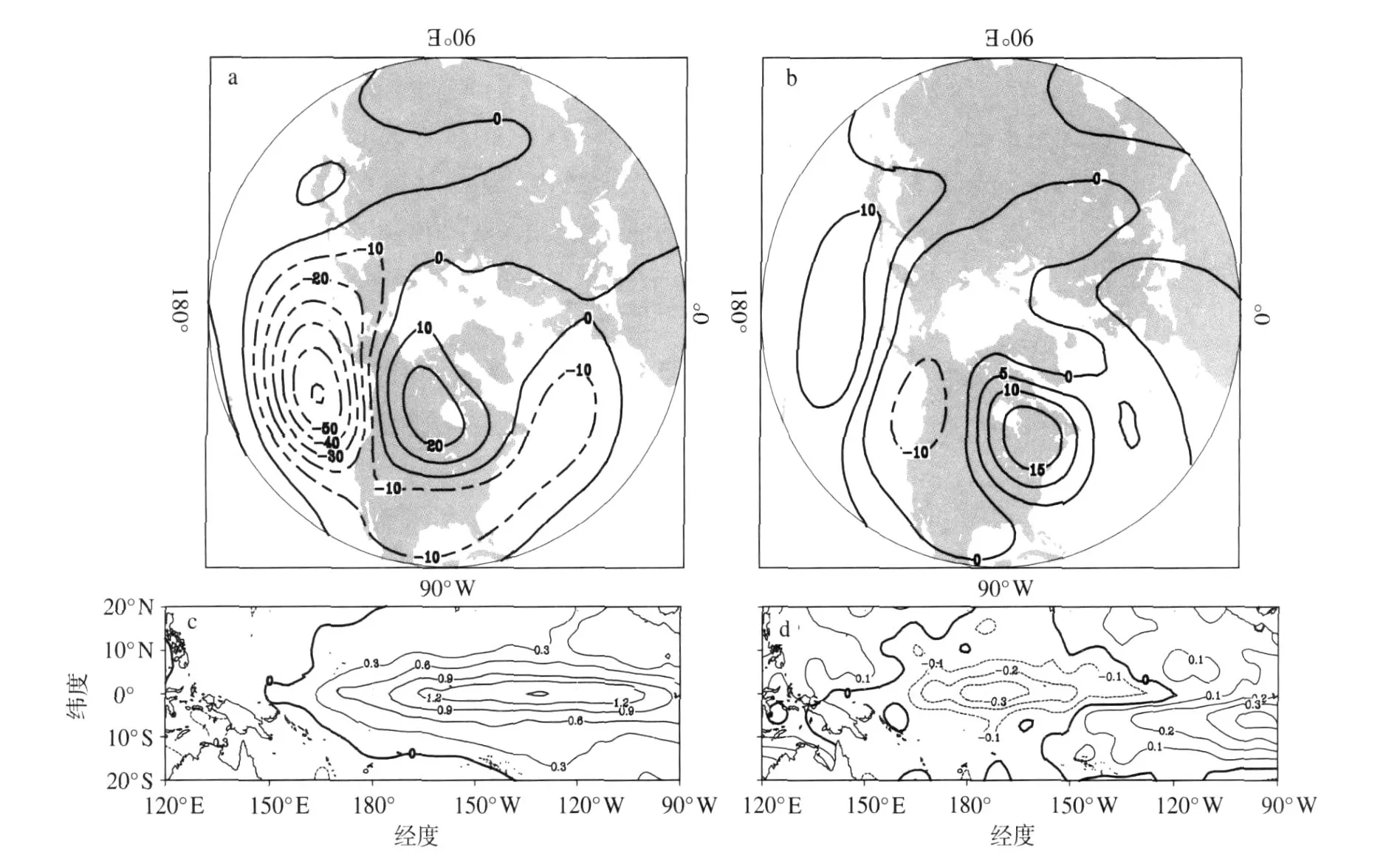
图2 预报的1—3月500 hPa高度场(a,b)与前期11月海温场(c,d)的SVD1(a,c)和SVD2(b,d)模态(各模态的强度相当于时间系数的1个标准差;(a)、(b)、(c)、(d)中等值线间隔分别为10 m、5 m、0.3℃、0.1℃;(c)和(d)中阴影区分别表示大于0.6℃、小于-0.1℃的SST异常)Fig.2 Forecast(a,b)JFM 500 hPa height and(c,d)previous November SST distributions of(a,c)SVD1 and(b,d)SVD2(The magnitude corresponds to one standard deviation of each time coefficient.The contour interval is 10 m for(a),5 m for(b),0.3℃for(c),and 0.1℃for(d).The shaded areas in(c)represent SST anomaly values greater than 0.6℃,whereas those in(d)smaller than-0.1℃)
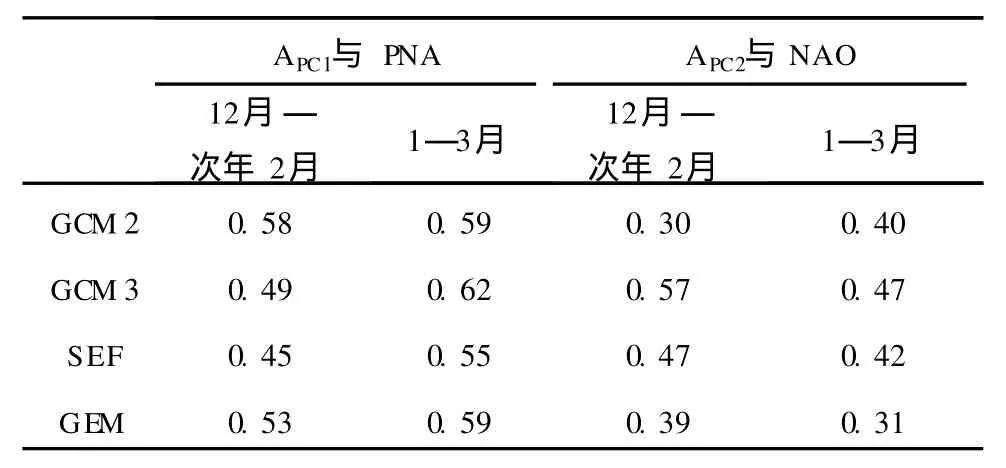
表1 模式SVD主模态的大气展开系数与观测的PNA和NAO指数的相关系数(相关系数大于0.3,表明通过0.05信度的显著性检验)Table1 Correlations between the atmospheric expansion coefficients of the leading forced SVD m odes and the observed PNA and NAO indices(A correlation coefficient that is larger than0.3passes the0.05significance level)
3 集合预报的订正方法
利用预报变量与上述外部强迫的大尺度模态的变化之间的联系,提出了一种后处理方法,构建了一个三参数的多元线性回归模型。对于任一格点,预报量为季节平均(12月—次年2月平均或者1—3月平均)的变量(例如:500hPa高度场、850hPa温度场、降水场),预报因子为模式预报中前三个SVD模态的大气分量的时间系数(即APC1、APC2和APC3)。进行SVD分析时,左右场分别为集合平均的12月—次年2月平均或者1—3月平均的北半球500hPa位势高度场和之前11月热带太平洋海表温度场,如前所述。在每个空间格点上,回归模型可以写为:

式中:a1、a2和a3分别是回归系数;ε是余数。在交叉验证理论框架中对历史观测资料和每个模式的SVD大气分量的时间系数(APCs)运用最小二乘原理来计算这三个回归系数,即:当计算要进行预报的那年的回归系数时,将该年的资料排除在外。因此,对统计模型进行训练的时候,利用的是与预报当年无关的资料。ε被认为是噪声,在模型训练和预报中忽略不计。由于大气环流模式对预报变量有它们自己的预报结果,我们将利用后处理方法(即(1)式)对预报结果进行订正之后的预报称之为订正预报。L in等[5]讨论了在订正过程中使用不同个数的SVD模态的效果,他们发现SVD第1模态和第2模态起主要作用,第3模态的贡献非常有限,而更高阶的模态则更加不重要。
图3a和3b分别给出了GEM原始的和经过订正的1—3月500hPa位势高度的集合预报的时间相关系数评分。由图可见,原来的集合平均预报在北太平洋、加拿大东部、墨西哥湾附近有一些预报技巧(图3a)。在订正预报中(图3b),预报技巧得到了显著提高。其他模式结果与此类似。相对于原预报,订正预报对模式的依赖程度较低。
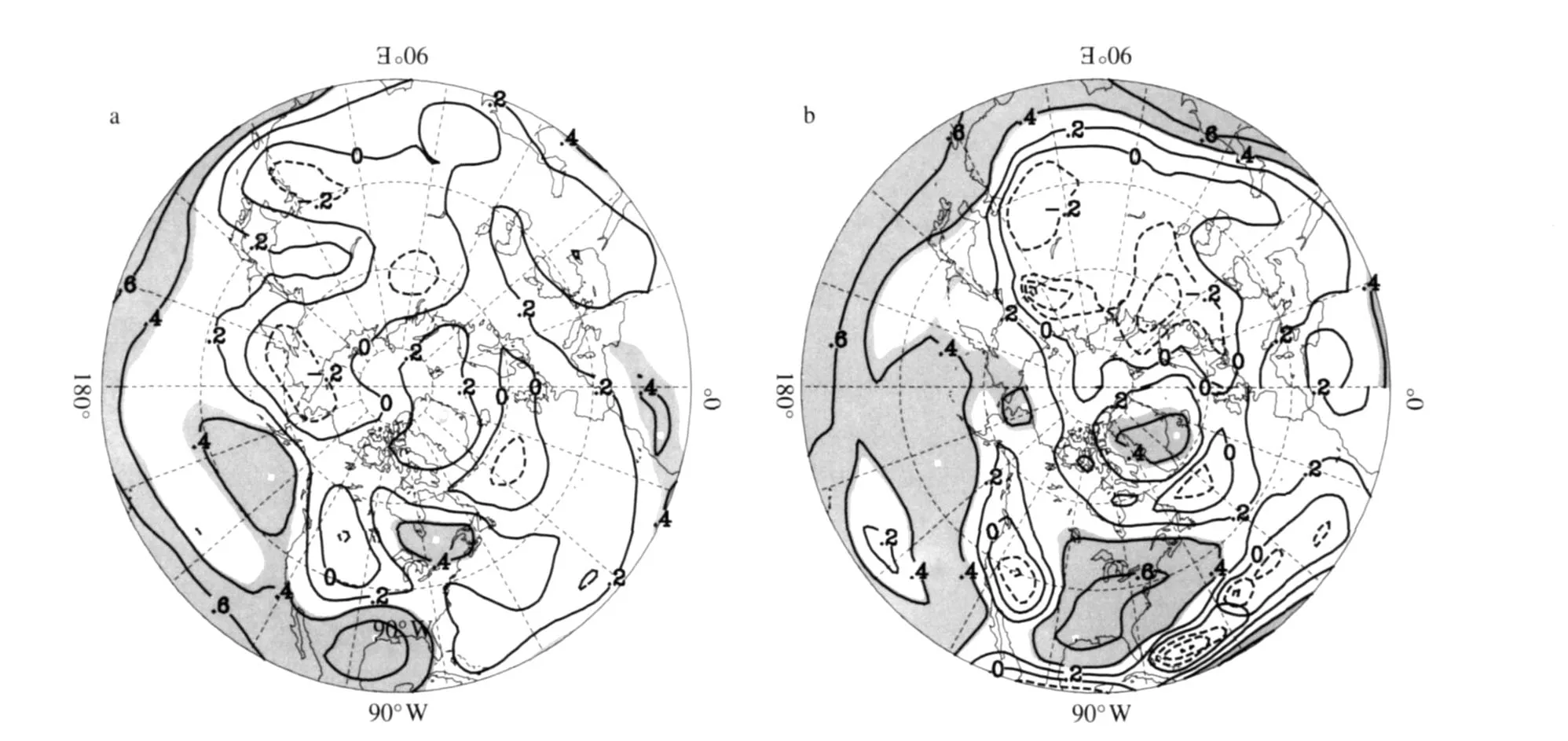
图3 全球环境多尺度模式(GEM)模拟的1—3月500hPa位势高度的相关系数评分(阴影区表示通过0.05信度的显著性检验) a.原始预报;b.订正预报Fig.3 Correlation scores for(a)the original ensemble forecast and(b)the corrected forecast of JFM500hPa geopotentialheight by GEM(Areas with statistical significance passing the0.05level as estimated by a Student t-test are shaded)
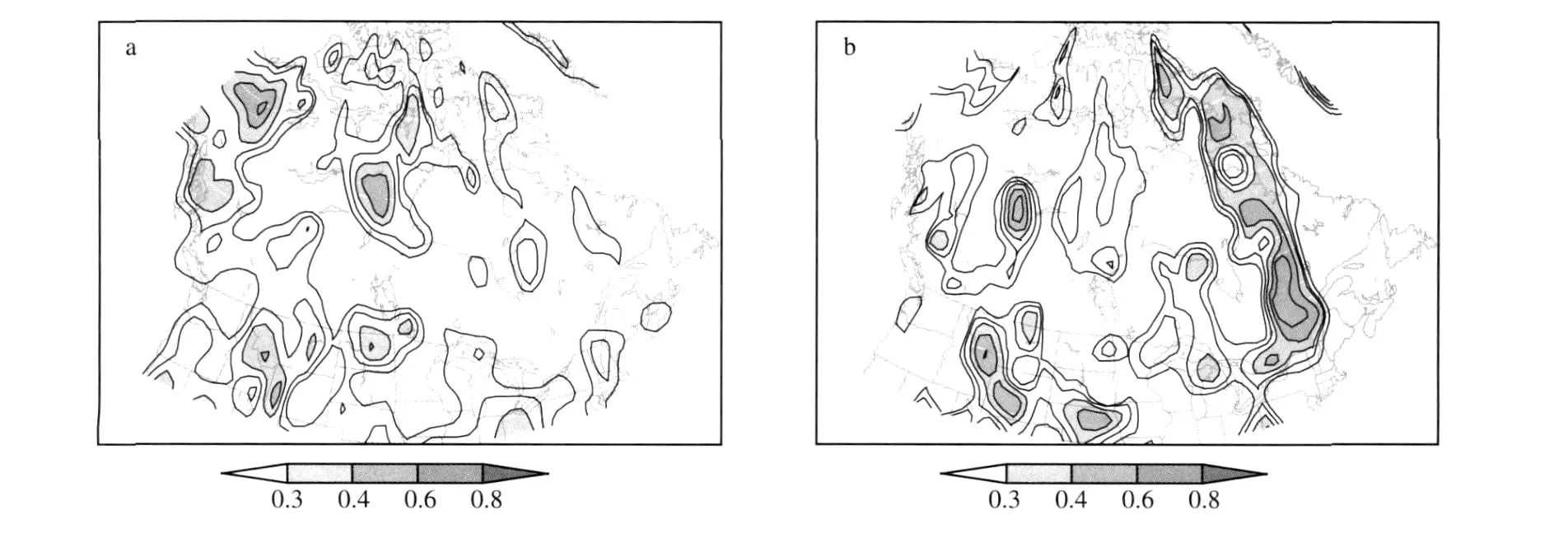
图4 4模式集合预报的1—3月平均降水的相关系数评分(等值线间隔为0.1;阴影区表示通过0.05信度的显著性检验)a.原始预报;b.订正预报Fig.4 Correlation scores for the JFM precipitation forecast by fourmodel combined ensemble for(a)original and(b)corrected forecasts(The contour interval is0.1.Areas with statistical significance passing the0.05level as estimated by a Student t-test are shaded)
应用上述后处理方法,进一步做了加拿大降水的季节预报。图4给出了原始的和经过订正的4个大气环流模式平均的1—3月降水预报的相关技巧分布。通过0.05信度的显著性检验的区域用阴影标识。由图4可见,原来的预报技巧非常有限(图4a);采用订正预报后,预报技巧得到了显著提高(图4b)。现在,各大气环流模式的预报技巧分布是基本一致的,主要位于两个区域:洛矶山东部以及魁北克—安大略省地区。
4 结论
本文介绍了一种对动力季节预报进行后处理的统计方法,该方法基于的一个事实是,气候异常受到与热带强迫有关的大尺度大气环流型的显著影响。PNA型和NAO型是北半球两个最重要的大气环流型。尽管它们的空间分布不能够被数值模式很好地模拟出来(特别是NAO型的空间分布),但是,对集合平均的(外界强迫的)500hPa位势高度场和用于强迫模式运行的热带太平洋海表温度进行SVD分析得到的主模态的展开系数却能够将它们的时间演变合理地模拟出来。
采用这种后处理方法后,北半球500hPa位势高度场的预报技巧与原来的预报技巧相比得到了显著提高。加拿大的降水季节预报也有明显提高,由此得到了洛矶山东部和魁北克—安大略省地区的可靠的季节降水预报。
致谢:谨以此文纪念我十分敬重的硕士导师朱乾根教授!同时,感谢G ilbert B runet和Jacques D erom e博士对我们相关文章所做的工作。感谢加拿大HFP项目的同事提供的数据。感谢倪东鸿编审将此文翻译成中文。
[1] Smith T M,Livezey R E.GCM systematic error correction and specification of the seasonal mean Pacific-North America region atmosphere from global SSTs[J].J Climate,1999,12:273-288.
[2] Feddersen H A,Navarra A,Ward M N.Reduction of model systematic error by statistical correction for dynamical seasonal prediction[J].J Climate,1999,12:1974-1989.
[3] M o R,Straus D M.Statistical-dynamical seasonal prediction based on principal component regression of GCM ensemble integrations[J].M on W ea Rev,2002,130:2167-2187.
[4] Kang I-S,Lee J-Y,Park C-K.Potential predictability of summer mean precipitation in a dynam ical seasonal prediction system with systematic error correction[J].J Climate,2004,17:834-844.
[5] L in H,Derome J,B runet G.Correction of atmospheric dynam ical seasonal forecasts using the leading ocean-forced spatial patterns[J].Geophys ResLett,2005,32,L14804,doi:10.1029/2005GL023060.
[6] L in H,B runet G,Derome J.Seasonal forecasts of Canadian w inter precipitation by post-processing GCM integrations[J].M on W ea Rev,2008,136:769-783.
[7] Jia X,L in H,Derome J.Improving seasonal forecast skill of North American surface air temperature in fall using a postprocessing method[J].M on W ea Rev,2010,138:1843-1857.doi:10.1175/2009MW R3154.1.
[8] Derome J,B runet G,Plante A,et al.Seasonal predictions based on two dynam ical models.A tmosphere-Ocean[J].2001,39:485-501.
[9] Boer G J,M cFarlane N A,Laprise R,et al.The Canadian Climate Centre spectral atmospheric general circulation model[J].A tmosphere-Ocean,1984,22:397-429.
[10] M cFarlane N A,BoerG J,B lanchet J-P,et al.The Canadian Climate Centre second-generation general circulation model and its equilibrium climate[J].J Climate,1992,5:1013-1044.
[11] Ritchie H.Application of the semi-Lagrangian method to a multilevel spectral prim itive-equation model[J].Quart J Roy Meteor Soc,1991,117:91-106.
[12] Ritchie H,Beaudoin C.Approximation and sensitivity experiments with a baroclinicsemi-Lagrangian spectral model[J].M on W ea Rev,1994,122:2391-2399.
[13] CôtéJ,Gravel S,Méthot A,et al.The operational CMC-MRB Global Environmental Multiscale(GEM)model:Part I-Design considerations and formulation[J].M on W ea Rev,1998,126:1373-1395.
[14] CôtéJ,Desmarais J-G,Gravel S,et al.The operational CMCMRB Global EnvironmentalM ultiscale(GEM)model:Part IIResults[J].M on W ea Rev,1998,126:1397-1418.
[15] Kalnay E,Kanam itsu M,Kistler R,et al.The NCEP/NCAR40-year reanalysis project[J].Bull Amer M eteor Soc,1996,77:437-471.
[16] Kreyscher M,Harder M,Lemke P.First results of the Sea Ice model Intercomparison Project(S IM IP)[J].Ann Glaciol,1997,25:8-11.
[17] Dewey K F,Heim R Jr.New data base:a digital archive of Northern Hemisphere snow cover[C]//Presented at Western Snow Conference,April19—23.Reno,NV,1982:9.
[18] Wallace J M,Guztler D S.Teleconnections in the geopotential height field during the Northern Hemisphere w inter[J].M on Wea Rev,1981,109:784-812.
[19] Bretherton C S,Smith C,Wallace J M.An inter comparison of methods for finding coupled patterns in climate data[J].J Climate,1992,5:541-560.
Improving Atmospheric Dynamical Seasonal Forecasts Using the Dom inant Ocean-forced Patterns
L IN Hai
(Meteorological Research Division,Environment Canada,2121 Trans-Canada,Dorval,Quebec H9P 1J3,Canada)
Seasonal forecast skill in a numerical model mainly comes from variability in forcing that is external to the atmosphere.Current General Circulation Models(GCMs)are usually not able to correctly generate the response patterns and amplitudes associated with external forcing,leading to forecast errors.This paper describes a post-processing approach that helps to reduce the systematic error and improve seasonal forecast skill.
dynamical seasonal forecast;ocean-forced patterns;numerical model
P435
A
1674-7097(2010)06-0641-06
2010-10-10;改回日期:2010-10-22
HaiLin,Research Meteorologist,Meteorological Research Division,Environment Canada,2121 Trans-Canada,Dorval,Quebec H9P 1J3,CANADA,hai.lin@ec.gc.ca.
林海.利用海洋强迫的大气主模态提高大气动力季节预报[J].大气科学学报,2010,33(6):641-646.Lin Hai. Improving atmospheric dynamical seasonal forecasts using the dominant ocean-forced patterns[J].Trans Atmos Sci,2010,33(6):641-646.
(责任编辑:倪东鸿)
