一个基于混沌理论的加密算法的设计

2010-10-16王晓英

赤峰学院学报·自然科学版 2010年2期

关键词：密码学随机性明文

王晓英

（赤峰学院数学学院，内蒙古赤峰 024000）

一个基于混沌理论的加密算法的设计

王晓英

（赤峰学院数学学院，内蒙古赤峰 024000）

本文提出了一种基于Logistic混沌系统的加密算法，以此来加密数字多媒体信息，实验表明混沌加密具有较好的安全性和伪随机性，即使密钥相差微小，经过混沌放大后也相差甚远，是一种行之有效的算法.

Logistic混沌系统；混沌加密；混沌序列

混沌是由简单的确定性非线性系统产生的伪随机行为，它的基本特征是伪随机、连续宽带功率谱和对初始条件十分敏感，这意味着即使是两个完全相同的混沌系统从几乎相同的初始条件开始演化，它们的轨道也很快变得互不相关.混沌的这种特性启示人们由此构造加密系统，于是人们展开了广泛的研究工作，混沌密码学领域出现了大量的研究文献.

最早将混沌学应用于密码学的思想可以追溯到1949年香农出版的经典文章“Communication Theory of Security System”，但那时他并不知道有“混沌”一词.自20世纪80年代以来，应用混沌系统构造新型密码系统的想法得到了越来越多的关注，这一想法来源于混沌系统和纯粹密码学系统之间的自然联系：强混沌系统的动力学特性大致对应着高强度密码学系统的某些安全特征；而具有良好混合性的传统密码系统又暗含着拟混沌现象.另一方面，从算术的观点来看，任何一种密码系统都可以看作是一个混沌系统或类混沌系统，因为完美的密码学特性是由确定加密过程产生伪随机不规则序列来保证的，这很像是由复杂的动力学系统产生混沌序列.

所以，用混沌系统来设计新型的密码是一种很自然的想法.混沌密码是传统密码的一种新型发展，有着广阔的前景.引入了混沌的密码系统不仅表现出许多优良的密码学特性，而且还具有丰富的源泉，另外，混沌方法能极大地简化传统密码的设计过程.因此，混沌密码学方法被列入现代密码学的重要研究前沿.混沌加密方法属于对称加密体制的范畴，其安全性取决于密钥流发生器即混沌系统所产生的信号与随机数的近似程度，密钥流越接近随机数安全性越高，反之则越容易攻破.

但是混沌密码的一些方法在理论上存在着缺陷，在实践过程中也存在一些不足，混沌加密方法目前还处于探索阶段.

1 混沌加密原理

我们利用混沌系统，可以产生周期无限长、非相关、类似噪声、又确定可以再生的混沌序列，这种序列难于重构和预测，从而使敌方和非法入侵者难于破译，非常适合应用于信息的加密，其随机性、抗破译能力均优于传统的随机序列.这些使得混沌序列能够成为一种优秀的加密序列，产生非常好的加密效果.混沌加密、解密框图如下：

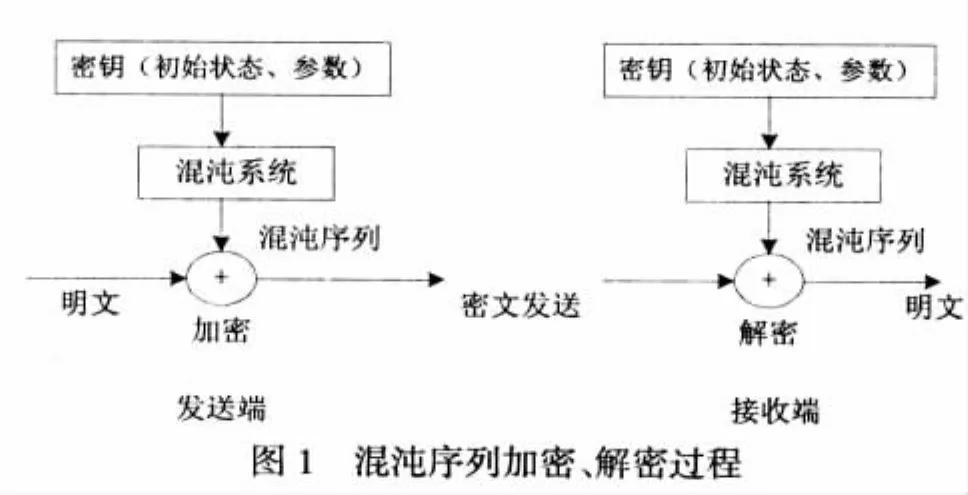
首先，利用混沌系统产生序列，再对混沌序列进行适当的处理，然后利用处理后得到的序列与明文进行作用，得到密文.密钥取为混沌系统的初始值或系统参数.

为了取得更好的加密效果，我们可以利用多种混沌系统对同一明文进行多次加密，还可以利用经典密码学的方法对序列进行加密处理，从而提高加密效果，极大地增加非法入侵者破译的难度.解密是加密的逆过程，我们可以利用密钥产生混沌序列，与密文进行相互作用从而恢复出明文信息.混沌序列加密方法的特点是：

(1)有非常好的随机性，类似噪声，难于破译，其随机性远远优于传统的随机序列发生器产生的随机序列；

(2)密钥空间大，混沌系统一般有多个参数；

(3)混沌系统难于重构，因此，混沌序列也难于重构，从而抗破译能力比传统的随机序列发生器产生的随机序列强.

(4)混沌序列产生方便，与非线性反馈移位寄存器相比，提供了更大的灵活性.

2 混沌加密方案设计

假设{Pn}是明文信息序列，{Kn}是密钥信息序列，由Logistic混沌方程迭代产生序列后，进行二值化处理后所得整数混沌序列，{Cn}是密文信息序列.

基于Logistic混沌映射的加密原理图如图2所示，解密过程是加密的逆过程.初始值x0和u是Logistic方程的参数，同时是加密系统的密钥参数K={x0,u}.

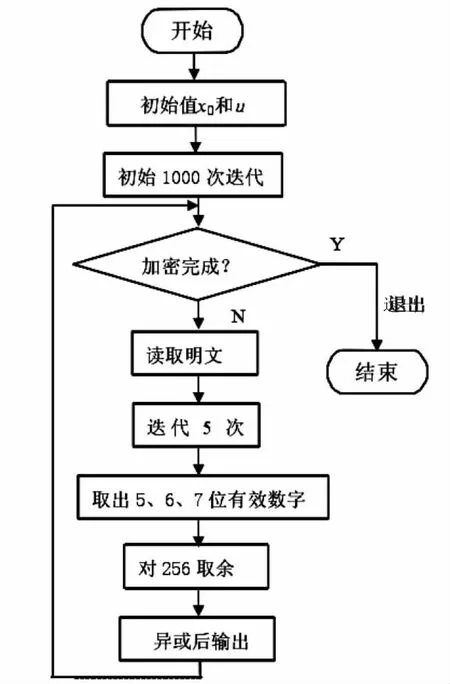
图2 Logistic混沌加密过程

因为混沌系统对初始条件的敏感依赖性，对于仅有微小差别的初值，混沌系统在迭代了一定次数后便会产生截然不同的混沌序列.为了使相近初始值的混沌序列互相间更加不相关，本方案的混沌序列经过1000次以上迭代后取值，可以有效地放大误差使得对初始条件的攻击无效，使加密效果更好，安全性更高.由于加密的是数字量，所以必须使用一种方法将这个由实数构成的序列{Xn}映射成由整数构成的伪随机序列，来充当加密密钥.这种映射中最简单的一种莫过于选取Xn小数点后的几位有效数字构成整数.

3 实验仿真

采用Logistic混沌系统，初值x0=0.1568942作为密钥，分支参数μ=4，迭代次数为100000次，经过1000次以上迭代后取值.下图为Logistic混沌序列对一幅256×256 Lena图像进行加密解密，仿真结果如图3所示.(a)是原始图像，加密后的结果如图(b)所示，采用相同的密钥解密后的结果如图(c)，当密钥存在微小的差别时，解密后的结果如图(d)所示.