改进的全水深非线性波传播模型及其模拟
2010-10-11洪广文冯卫兵
张 俞,洪广文,冯卫兵
(1.河海大学海岸与海洋工程研究所,江苏南京 210098;2.河海大学港口海岸与近海工程学院,江苏南京 210098)
目前波浪传播模型主要沿着完全频散性的线性缓坡方程(MSE)[1]及其扩展(EMSE)[2-5]与弱频散性的非线性Boussinesq型方程[6]及其扩展[7-8]2种典型模型不断发展.完全频散性的线性缓坡方程及其扩展模型主要应用于大范围水域波浪传播计算,其优点是计算简便,可计算大范围水域,缺点是对浅水域、非线性作用强的区域特别是破碎区域难以有效模拟.Boussinesq型方程及其扩展模型主要用于浅水水域波浪的变形计算,能够很好地反映其非线性特性,但是计算难度大,较难应用于深水域的波浪计算.为此,能够同时兼顾频散特性和浅水非线性特性,较全面、精确模拟波浪传播的全水深方程波浪传播模型成为新型的波浪模拟途径.
全水深方程波浪传播模型最早由Nadaoka等[9-10]提出,但其只适用于无流情况且未考虑能耗与地形因子影响.洪广文等[11-12]基于格林公式和变分法提出了含有能量系数的水流中联合折射-绕射线性模型,随后扩展为缓变流场、水位和水深的非线性模型,并证明在浅水域可以转化为Boussinesq型方程、KdV方程、Airy浅水波方程,在深水域可化为非线性缓坡方程.吴中等[13]利用该非线性模型进行了较系统的计算验证;张俞等[14]也利用其计算了考虑波浪破碎及摩阻损耗的单坡地形上波浪传播,考虑了反映地形坡度与曲率因子J的影响.
本文在长波上非线性重力表面波传播数学模型基础上建立了保留了三阶项的数学模型及其求解模式,并且在方程中(kη)2项近似取为2.采用Berkhoff试验地形和用于验证Boussinesq型方程模型的单坡地形进行模拟计算,并将结果与试验值及线性、二阶模型结果相比较,验证三阶全水深非线性数学模型的计算精度及适用性.
1 全水深非线性波传播数值模型
1.1 三阶非线性数学模型
基于长波上非线性重力表面波传播数学模型[12],保留三阶项可得无流情况下三阶非线性数学模型,控制方程如下:


其中
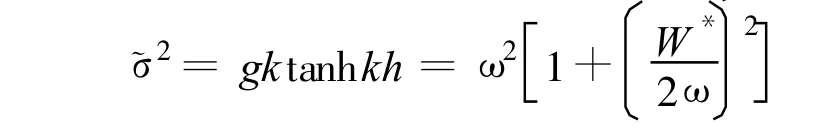
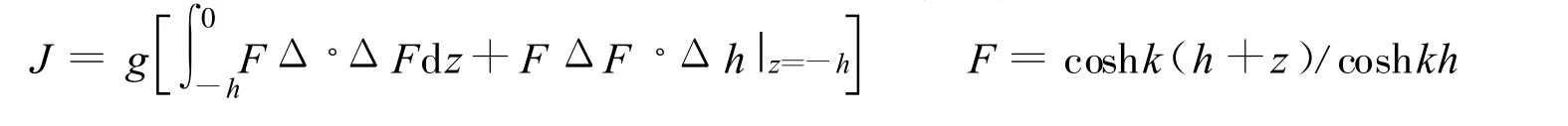
式中:x,y——平面坐标,置于静水面处;z——垂直坐标,竖直向上为正;h——当地水深;Φ——二维复值波动势函数;η——复值波面函数;W*——能量系数,包括能量输入与能量损耗(包括摩阻损耗和破波损耗);J——反映水底地形坡度与曲率有关的参数[12,14];k——波数,~c,~cg,~σ——波速、波群速和考虑能耗的相对圆频率;ω——绝对圆频率;g——重力加速度.
1.2 二阶非线性模型

1.3 线性传播数值模型
略去高阶项,由方程(1),(2)可得如下线性模式控制方程:
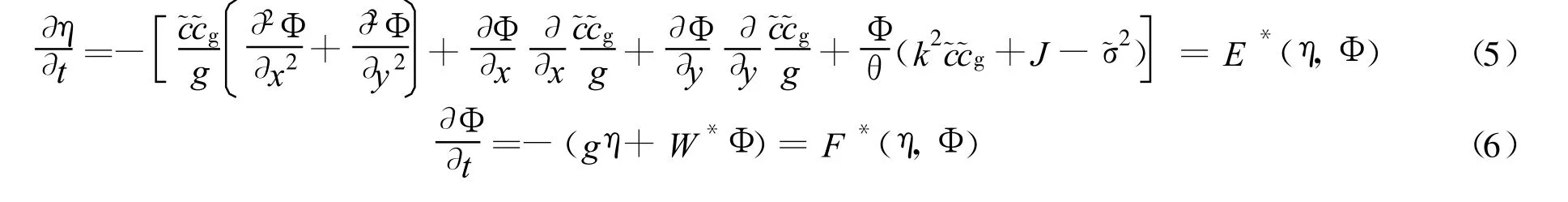
1.4 边界条件
为了使得入射条件与非线性模型控制方程组相匹配,本文的入射边界采用Stokes二阶形式:
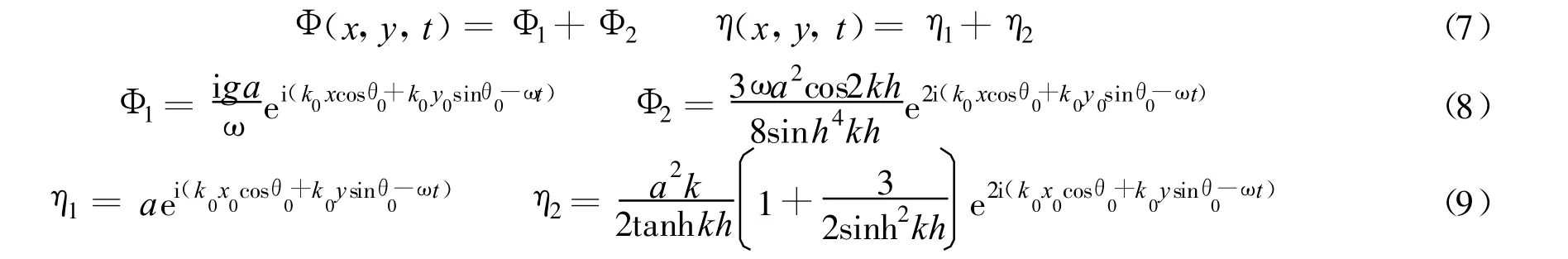
式中:y=y0——入射边界;θ0——入射波的波向与 x轴的夹角;a——入射波的振幅;k0——波数.出流边界采用消波层消波与统一出流边界相结合的方式[14].
1.5 初值条件
初始情况(t=0)除入射边界外,其余水域 Φ,η均为0.
1.6 控制方程的数值解法
采用可变网格的预测-校正-迭代的Crank-Nicolson算法[14].为了增加计算的稳定性,本文程序设计上采用将线性项与非线性项分离,先由线性模型计算至稳定,再将线性结果作为非线性初值进行迭代计算.
2 模型验证与分析
2.1 椭圆浅滩地形
1982年,Berkhoff[1]在水力实验室针对均匀斜坡上布置一椭圆形浅滩的地形进行了波浪物理模型试验,以验证线性缓坡方程的计算结果.试验采用的波周期为T=1.0s,入射波高为H0=0.0464m,并取得了8个断面的实测资料.
Berkhoff试验地形如图1所示,本文的计算区域为 0 m<x<21.5m,0m<y<20m,波浪垂直y断面正向入射.将该计算区域坐标转换到椭圆中心,可得

在新坐标系中斜坡上水深:
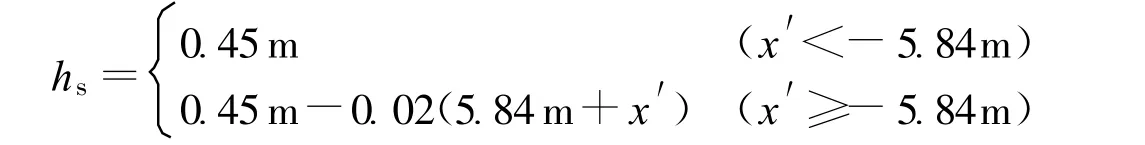
斜坡加上椭圆浅滩后的地形为

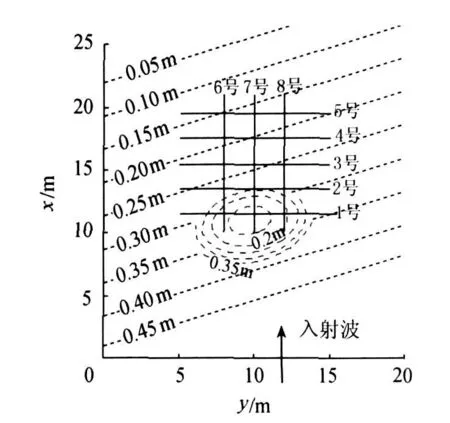
图1 Berkhoff椭圆浅滩地形试验水深等值线及断面分布Fig.1 Sketch of Berkhoff's test bathymetry
模型中空间网格步长为Δx=Δy=0.1,时间步长取Δt=T/60,计算总时长为32T.非线性模式入射边界 Φ采用Stokes二阶波的形式给定,线性模式 Φ采用Stokes一阶波的形式 Φ1给定,即 Φ=Φ1;左右边界及出流边界均采用消波层与统一边界条件进行处理,消波层长度为波长的2倍;计算达到稳定后对各计算点波面时间过程线采用上跨零点法求取波高.各断面的相对波高结果见图2(图中H为波高,H0为各组况下的入射波高).图3和图4为整个水域的波高等值线图及波面影像图.
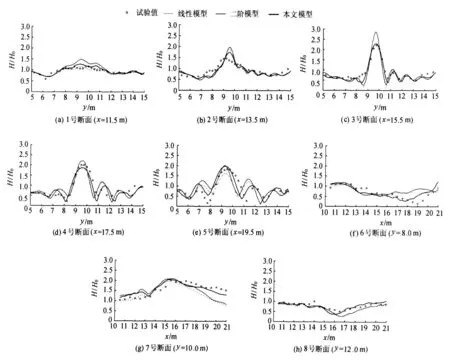
图2 1~8号断面相对波高计算值与试验值比较Fig.2 Comparison between measured and computed relative wave heights for section No.1—No.8
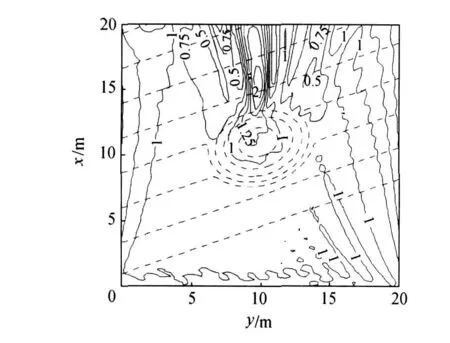
图3 数值模拟的相对波高等值线(单位:m)Fig.3 Contours of simulated relative waveheights(unit:m)
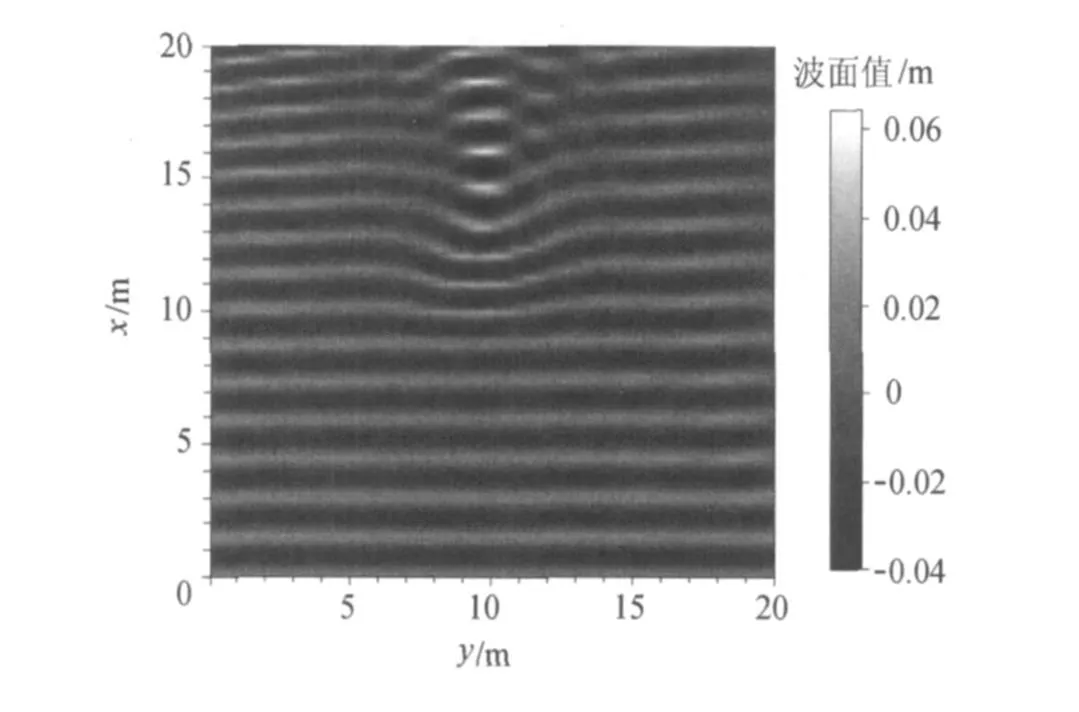
图4 t=32T瞬时波面影像Fig.4 Instantaneous wavesurface elevation for t=32T
由图2可见,本文模型的结果优于二阶模型及线性模型结果,特别是在水深较浅的5号以及6~8号的浅水处.由图3和图4明显可以看出,随着水深变浅,波向朝着垂直于等深线的方向传播,且在椭圆地形附近发生辐聚,符合波浪的变形趋势.
2.2 单坡地形
采用文献[7]中为验证Boussinesq型方程扩展模型进行的单坡水槽波浪传播试验资料作为验证依据,其试验模型布置如图5所示.该水槽有效长度30m、水深0.36m,在水槽末端设1∶34.26的斜坡.入射波采用表1中给出的5种破波形态的波要素.

图5 Hansen与 Svendesen试验地形Fig.5 Layout of Hansen and Svendesen's test bathymetry

表1 Hansen与Svendesn试验入射波参数Table1 Parameters of incident waves for Hansen and Svendesen's tests
本文模型中入射处采用非线性入射条件,出流边界处采用消波层与统一边界条件相结合的方式处理.各模型中的空间步长随该水深处对应的波长呈连续性变化,Li/Δxi≥7,Δt=T/50~T/100.
波浪破碎采用试算的方法先确定最初的破碎点.破碎点确定后,破碎点后采用公式

式中 ω为绝对圆频率;系数S参照文献[15]和Bettjes等[16]破碎公式调试确定.对于表1中所取5组波要素,S依次取0.6496,0.6496,0.4974,0.2210,0.1240,破碎点前=0,重新进行整个水域 Φ,η的计算,得到波高值.破碎后的波参数与试验结果吻合良好.
由图6结果可以看出,斜坡上水深较深段,线性模型结果尚能满足要求,但随着水深变浅,线性模型结果明显偏小,不能有效体现波浪的传播变形规律;本文模型与二阶模型计算结果相当,与试验值吻合良好,说明该三阶修正是合理的.值得一提的是,Kirby对线性缓坡方程进行非线性扩展[2],其模型对Berkhoff试验地形验证后得到了很好的结果,但是该修正用于计算单坡地形,结果并不理想.

图6 计算波高与试验值比较Fig.6 Comparison between measured and computed wave heights
3 结 论
a.本文模型能同时兼顾非线性与频散性特性,模型中W*能考虑能量的输入与耗散.
b.本文模型对“长波上非线性重力表面波传播数学模型”保留至3阶精度,并用2替代 η2,采用含有松弛因子的Crank-Nicklson算法,入射边界采用Stokes非线性波输入改善与模式的匹配性,出流条件采用消波层与统一边界条件相结合的方法,模型计算后获得稳定的波高结果.
c.Berkhoff试验地形验证结果表明,本文模型与试验值吻合度有所提高,其效果类似于Kirby修正;单坡地形验证结果表明,本文模型能模拟波浪由深水至浅水直至破碎的过程,所作的修正是合理的.
[1]BERKHOFF J C W.Computation of combined refraction-diffraction[C]//Proceeding 13thConference on Coastal Engineering.Vancouver:ASCE,1972:471-490.
[2]KIRBY JT,DALRYMPLE RA.Verification of a parabolic equationfor propagation of weakly nonlinear waves[J].Coastal Eng,1984,8:219-232.
[3]HSUT W,WEN CC.A parabolic equation extended to account for rapidly varying topography[J].Ocean Engineering,2001,28(11):1479-1498.
[4]PAN Jun-ning,HONGGuang-wen,ZUOQi-hua,et al.Verification of a numerical harbor wavemodel[J].China Ocean Engineering,2007,21(4):647-658.
[5]张扬,李瑞杰,张素香.波浪Boussinesq方程与缓坡方程的比较[J].河海大学学报:自然科学版,2005,33(5):588-591.(ZHANG Yang,LI Rui-jie,ZHANG Su-xiang.Comparasion of boussinesq equation with mild slope equation[J].Journal of Hohai University:Natural Science,2005,33(5):588-591.(in Chinese))
[6]PEREGRINEDH.Long waves on a beach slope[J].JFluid Mech,1967,27(4):815-827.
[7]KENNEY A B,CHEN Q,KIRBY JM,et al.Boussinesq modeling of wave transformation,breaking and runup.I:1D[J].Journal of Waterway,Port,Coastal and Ocean Engineering,2000,126(1):39-47.
[8]LI B.Wave equations for regular and irregular water wave propagation[J].Journal of Waterway,Port,Coastal and Ocean Engineering,2008,134(2):121-142.
[9]NADAOKA K,BEJI S,NAKAGAWA Y.A fully-dispersive nonlinear wave model and its numerical solutions[C]//Proceeding of the 24thInternational Conference on Coastal Engineeing.Kobe:ASCE,1994:427-441.
[10]ISOBE M.Time-dependent mild slope equation for random waves[C]//Proceeding of the 24thInternational Conference on Coastal Engineering.Kobe:ASCE,1994:285-299.
[11]HONGGuang-wen.Mathematical models for combined refraction-diffraction of wave on non-uniform current and depth[J].China Ocean Engineering,1996,10(4):433-454.
[12]洪广文,吴中,张俞.长波上非线性重力表面波传播数学模型[C]//第14届全国海岸工程学术讨论会论文集:上.呼和浩特:海洋出版社,2009:21-34.
[13]吴中,洪广文,张洪生,等.完全频散性非线性波数值模型及应用[C]//第14届全国海岸工程学术讨论会论文集:上.呼和浩特:海洋出版社,2009:448-457.
[14]张俞,洪广文,冯卫兵,等.考虑能量损耗的全水非线性波传播[C]//第14届全国海岸工程学术讨论会论文集:上.呼和浩特:海洋出版社,2009:465-472.
[15]DALLY W R,DEAN RG,DALRYMPLE R A.Wave height variation across beaches of arbitrary profile[J].JGeophys Res,1985,90(C6):11917-11927.
[16]BATTJESJA,JANSSEN J PF.Energy loss and set-up due to breaking of random waves[C]//Proceeding 16thConference on Coastal Engineering.Hamburg:ASCE,1978:569-587.
