基于灵敏度分析的地下水数值模拟精度适应性评价

鲁程鹏,束龙仓,刘丽红,刘佩贵,董贵明

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.合肥工业大学土木与水利工程学院,安徽合肥 230009;3.中国矿业大学资源与地球科学学院,江苏 徐州 221116)

随着地下水流基础理论的完善和计算机技术的不断发展,地下水数值模拟技术日趋成熟,地下水数值模型已成为地下水科学发展中一个强有力的工具[1].数值模型对定解问题的边界条件以及初始条件的要求较解析模型低,适应于各种复杂的地下水流系统问题的求解.数学理论已证明,在符合一定的时间、空间步长要求下,数值解趋近于解析解[2].但是,通过对自然条件的概化得到的数值模型的解究竟与真实情形相差多少,还是必须通过与实测资料的对比来定量评价模拟结果的优劣.地下水领域使用最为广泛的观测资料是地下水位观测资料.对数值模型而言,模拟结果的精度适应性及参数灵敏度是极其重要的2个方面.模拟精度的适应性是指模拟精度随参数变化而做出的响应;参数灵敏度是指模型输出在参数摄动条件下的响应.两者存在以下差别:一是参数初值的选取对于参数灵敏度分析而言可以是任意的,但是对于精度适应性评价来说则是在参数率定完成之后,在其优值附近进行评价;二是评价指标的选取在精度适应性评价中局限于模拟值与观测值之间的拟合误差评价,而灵敏度分析则可以选取任意的模型输出.

长期以来,地下水数值模拟精度评价都是根据区域内观测井实测水位与计算水位的差值及拟合程度来判定模型的精度和适应性.常用的评价方法是通过最小二乘法计算水位观测曲线与计算曲线之间的离差平方和来进行定量分析,实际也常常通过直观比较2条曲线的拟合程度来进行分析,主观评定模型拟合的好坏.但是,主观评定往往受到评定者的主观喜好和个人经验等因素的制约,不同建模者将会得到不同的模型率定参数,另外通过客观的最小二乘法或者对数及加权求和方法都存在标准化的问题,不同的观测井,不同时间和区域,其比较基准不一样,因而不能对所得结果统一进行比较.

Nash-Sutcliffe效率系数E ns及平均相对误差E mr在径流过程的相似性和拟合精度评价方面具有常用离差平方和所不具备的标准化特点[3].然而,目前在地下水领域模型模拟精度评价方面尚无采用该类标准的先例.因此,本文以 Ens和 Emr作为评价标准,讨论地下水数值模型模拟结果的精度适应性,并采用Morris方法[4]对模型率定参数的适应性和参数灵敏度进行评价.

1 适应性评价方法

1.1 Morris方法

通过灵敏度分析可以评价模型输出对模型参数的响应程度.灵敏度分析的方法主要有2种:一种为传统的扰动分析法;另一种为在现代环境系统中更为有效的区域灵敏度分析方法[5].这2种方法有不同的应用范围,实施难度也不同[6].扰动分析法中最常用的是Morris方法.Morris方法选取模型中1个变量Pi,其余参数值固定不变,在修正方法中采用参数自变量Pi以设定好的变幅变化,运行模型得到目标函数y(P)=y(P1,P2,P3,…,Pn)的值,用影响值Si判断参数变化对输出值的影响程度[7-9].Si的计算公式为

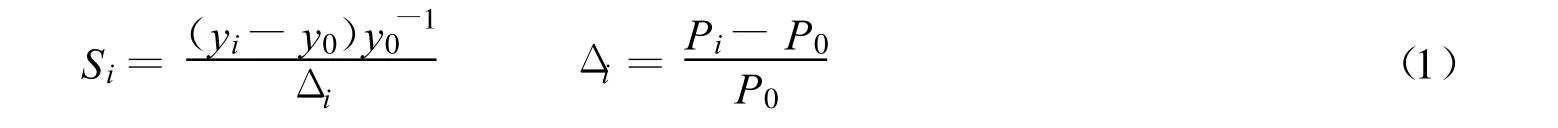
式中:yn——参数变化后的输出值;y0——参数变化前的输出值;P0——初始参数;Δi——参数 Pi相对于参数P0的变幅.灵敏度判别因子S取多个影响值的平均值[8],即

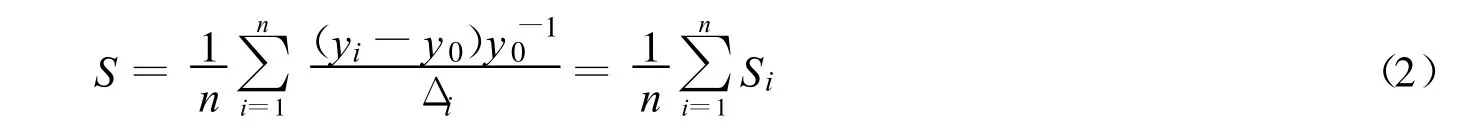
式中n为模型运行次数.

1.2 模拟精度的适应性标准

地下水模型中的输出变量往往是一系列随时间变化的量,Morris方法输出变量yi的选取比较困难.这里以Ens和Emr作为输出标准,一方面可以评价数值模拟精度的适应性,另一方面通过Morris方法可以得到模型参数的灵敏度.E ns和E mr的计算公式为

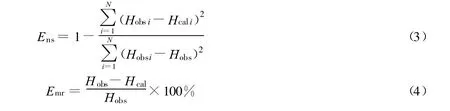
式中:Hobsi——某时刻观测水位;Hcali——某时刻计算水位;¯Hobs——观测水位平均值;¯Hcal——计算水位平均值.

本文定义SN为数值模拟精度的适应性指标,定义SP为参数适应性判别因子,SP值的大小反映了该参数在参数率定结果附近的综合灵敏度,S P越大灵敏度越高.S N和S P的计算公式为

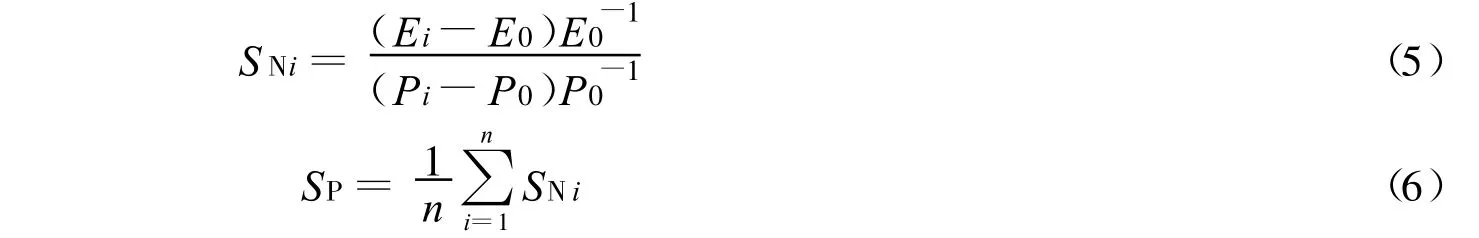
式中 Ei为参数Pi条件下的Ens或 Emr值.

显然,计算水位与实测水位一致时,效率系数取得最大值1.一般情况下,效率系数的变化范围为0～1.若效率系数为负值,则说明模型精度很差.式(3)是目前水文模拟中最常用的目标函数之一.利用该目标函数可以很好地控制模拟过程.但在洪水过程模拟中,可能洪峰预报精度较高,整个过程将错位1～2个时段[2].另外,选取Emr协同评价模型模拟精度.

1.3 数值模拟精度适应性评价

对复杂非线性系统而言,参数初值不同,相同变幅引起的系统响应也不一样,并且在同一位置上增大或减小相同幅度的参数值,对模型的影响也不一定相同[10-13].对建模者来说,最为关注的是模型参数在最优值附近的灵敏度问题,即模型模拟精度的适应性问题.最优值附近微小扰动对模型运行结果的影响是模型模拟精度适应性最直接的评价指标.精度适应性判别因子参照文献[14]中的标准化灵敏度取值,见表1.

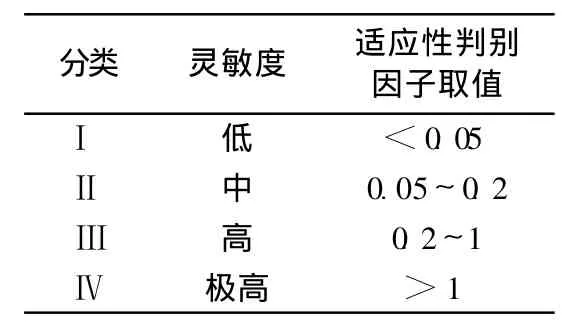
表1 精度适应性判别因子取值Table 1 Values of sensitivity factors

本研究以离差平方和最小的拟合结果作为模拟精度适应性评价初值,并采用Morris方法,分别以E ns和Emr作为模型输出来评价模拟精度的适应性和参数的灵敏度,同时以时间序列的观测水位灵敏度分析结果作为灵敏度分析的补充依据,讨论参数变化对模型计算水位的影响.

2 计算步骤及结果

2.1 数值模型

本文以在贵州普定进行的某次抽水试验数据作为研究基础,通过Visual Modflow建立地下水数值模型,并采用该数值模型模拟该次抽水试验全过程,以抽水井内水位动态资料作为模型验证和评价资料.该次抽水历时4h,水位变化主要分为抽水下降段、基本稳定段和水位恢复段3个过程.该次试验的抽水井为潜水井,最大水位降深为0.93m,相对于含水层厚度来说变化不大,所以选用单层均值非稳定流模型进行模拟.模型边界设置充分大,主要参数为渗透系数K和给水度μ.采用Visual Modflow中参数估计模块按照观测值与计算值的离差平方和最小的标准率定模型参数,结果为K=309 m/d,μ=0.2.观测水位与计算水位过程如图1所示,此参数条件下Ens=0.845,Emr=5.84%.

2.2 模拟精度适应性分析

将K=309m/d,μ=0.2作为适应性分析的初值,分别对K和μ进行增减变化,具体选择依据E ns和E mr的变化情况而定,其中参数K的变幅范围为-20%～100%,参数 μ的变幅为-50%～100%.Ens,Emr与K,μ变幅的关系如图2和图3所示.

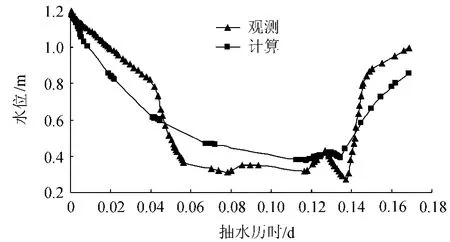
图1 观测水位与数值模型优化参数下的计算水位过程线Fig.1 Comparison of hydrographs of observed and calculated water levels with optimum parameters

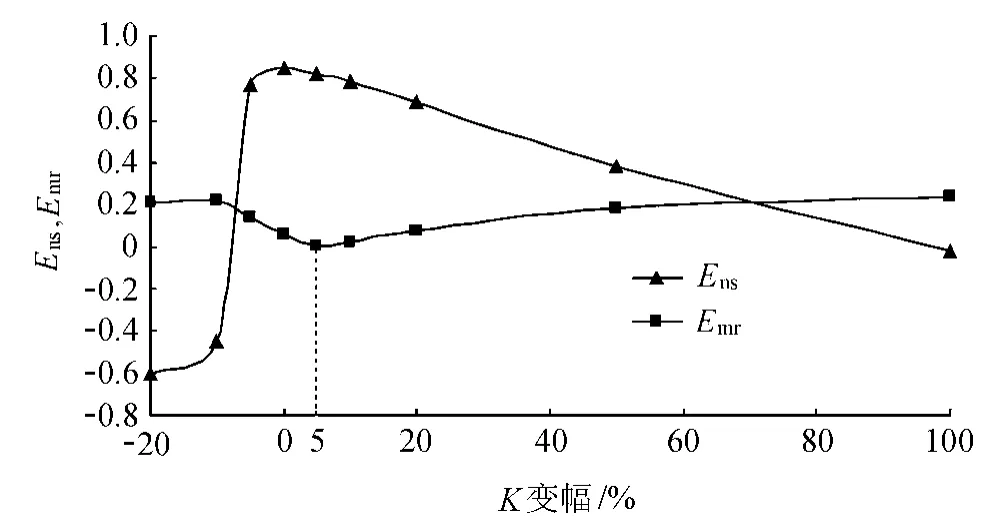
图2 E ns,E mr与 K变幅的关系Fig.2 Relationship between E ns,E mr and K

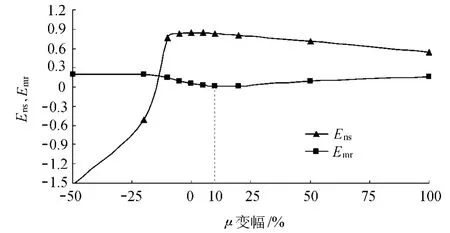
图3 E ns,E mr与 μ变幅的关系Fig.3 Relationship between E ns,E mr andμ

从图2可以看出,以离差平方和最小作为判断依据的率定结果与以Ens作为判断依据的率定结果基本一致,而与以平均相对误差Emr作为判断依据的率定结果分别相差不到5%和10%.这表明K的最优值在初值K0～1.05K0之间选取比较合理,μ的最优值在μ0～1.1μ0之间选取比较合理.若参数增大和减小幅度相同,则参数增大时模型的精度变幅比参数减小时模型的精度变幅要小.利用式(5)计算得到的SN与K,μ变幅的关系如图4所示;利用式(6)计算得到的K和μ的S P值分别为2.38和1.35.

从图4可以看出:当K和μ增大时,SN变化较小;而当K和μ减小时,SN变化很大.对比计算得到的SP值与表1,可以发现K和μ的灵敏度均极高,并且K的灵敏度高于μ.由此可知,参数优化初值确定后,K和μ的微小变化均会给模拟精度带来很大影响.

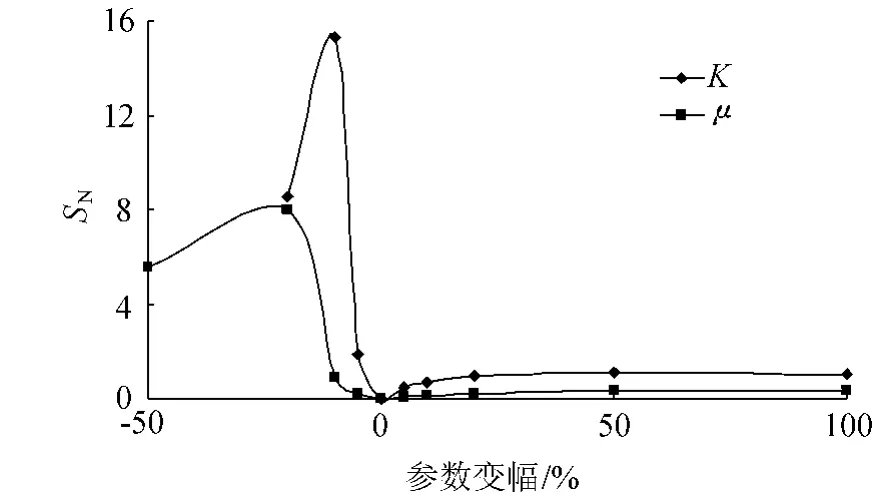
图4 S N与参数变幅的关系Fig.4 Variation of adaptability index S N with parameters K andμ

为了进行抽水过程的参数灵敏度分析,利用式(1)计算了影响值Si,其中yi为对应于每一时刻的模型计算水位值,y0则是初始参数对应的某一时刻计算水位值.整个时间序列不同变幅K和μ的Si计算结果如图5和图6所示.

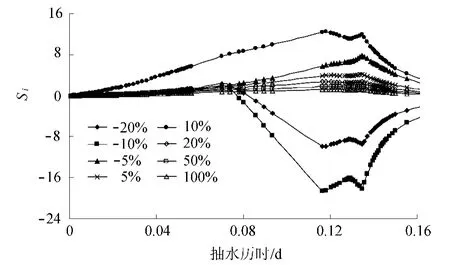
图5 K的Si计算结果Fig.5 Sensitivity curves of K

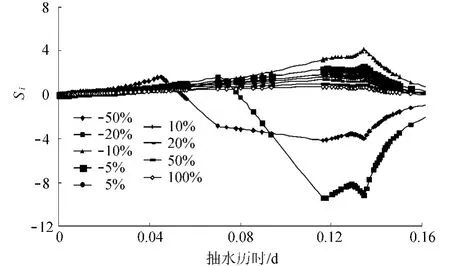
图6 μ的Si计算结果Fig.6 Sensitivity curves ofμ

比较图5和图6可以看出:(a)在模拟期内,K的灵敏度均高于μ,其值约为后者的2倍.(b)在模拟期的初始阶段,井内水位变化及其对含水层的影响范围较小,K与μ的灵敏度均较小;随着模型计算水位降深的增加,计算水位对参数灵敏度指标值开始增大,初始阶段不敏感的参数,模拟后期也具有较高的灵敏度.(c)在模拟后期,水位降深值又开始减小,随之参数的灵敏度又有适当的降低.因此,在率定模型参数时,应注意模型高水位降深期间,水位计算值与观测值的差别.另外,从参数不同变幅的灵敏度变化曲线来看,K的变幅在-20%～20%之间时,K的灵敏度值较大,但当K的变幅大于或等于20%时,K的灵敏度开始降低;μ的变幅在-50%～-5%之间时,μ的灵敏度值较大,而 μ的变幅在-5%～100%之间时,μ的灵敏度开始降低,灵敏度值较小.由此也可以得出在参数初值取值不同的条件下,其灵敏度分析结果有所差异的结论.

3 结 论

a.基于Morris方法的逐步改变参数变幅的适应性评价方法可以有效地评价优化参数初值附近的模型模拟结果的精度适应性.以Nash-Sutcliffe效率系数与平均相对误差作为模拟结果的精度评价标准,所得到的最优值存在差异.

b.地下水模型的时间序列灵敏度分析结果表明,在模拟期初始阶段水位降深值较小时,参数灵敏度较小,并且参数变幅不同,参数灵敏度随时间的变化过程也不同,甚至差异较大.

[1]郝治福,康绍忠.地下水系统数值模拟的研究现状和发展趋势[J].水利水电科技进展,2006,26(1):77-81.(HAO Zhi-fu,KANG Shao-zhong.Current situation and development trend of numerical simulation of groundwater system[J].Advance in Science and Technology of Water Resources,2006,26(1):77-81.(in Chinese))

[2]李庆扬,王能超,易大义.数值分析[M].4版.北京:清华大学出版社,2001.

[3]张建云,王国庆.气候变化对水文水资源影响研究[M].北京:科学出版社,2007.

[4]CHRISTIAENSK,FEYEN J.Useof sensitivity and uncertainty measures in distributed hydrological modeling with an application to the MIKE SHE model[J].Water Resources Research,2002,38(9):1-15.

[5]徐爱兰,姚琪,王鹏.基于太湖数字流域系统的水质模型参数灵敏度分析[J].水利科技与经济,2007,13(1):17-19.(XUAilan,YAOQi,WANG Peng.Sensitivity analysis for parameters of water quality model based on digital valley system of Taihu Basin[J].Water Conservancy Science and Technology and Economy,2007,13(1):17-19.(in Chinese))

[6]王建平,程声通.软计算技术在环境复杂模型参数识别中的应用研究[J].系统工程理论与实践,2006(2):118-126.(WANG Jian-ping,CHENG Shen-tong.Parameter identification of complicated environment model using the soft-computing approach[J].2006(2):118-126.(in Chinese))

[7]FRANCOSA,ELORZA F J.Sensitivity analysis of distributed environmental simulation models:understanding the model behaviour inhydrological studies at the catchment scale[J].Reliability Engineering and System Safty,2003,79(2):205-218.

[8]ZADOR J,ZSELY I G,TURANYI T.Local and global uncertainty analysis of complex chemical kinetic systems[J].Reliability Engineering System Safety,2006,91(10/11):1232-1240.

[9]郝芳华,任希岩,张雪松,等.洛河流域非点源污染负荷不确定性的影响因素[J].中国环境科学,2004,24(3):270-274.(HAO Fang-hua,REN Xi-yan,ZHANG Xue-song,et al.Uncertain affecting factor of the non-point source pollution load[J].China Environmental Science,2004,24(3):270-274.(in Chinese))

[10]黄金良,杜鹏飞,何万谦,等.城市降雨径流模型的参数局部灵敏度分析[J].中国环境科学,2007,27(4):549-553.(HUANG Jin-liang,DU Peng-fei,HE Wan-qian,et al.Local sensitivity analysis for urban rainfall runoff modeling[J].China Environmental Science,2007,27(4):549-553.(in Chinese))

[11]李森,陈家军,叶慧海,等.地下水流数值模拟中随机因素的灵敏度分析[J].水利学报,2006,37(8):977-984.(LI Sen,CHEN Jia-jun,YE Hui-hai,et al.Analysis on sensitivity of stochastic factors in numerical simulation of groundwater flow[J].Journal of Hydraulic Engineering,2006,37(8):977-984.(in Chinese))

[12]束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析[J].河海大学学报:自然科学版,2007,35(5):491-495.(SHULong-cang,WANGMao-mei,LIU Rui-guo,et al.Sensitivity analysis of parameters in numerical simulation of groundwater[J].Journal of Hohai University:Natural Sciences,2007,35(5):491-495.(in Chinese))

[13]SHU Long-cang,LIU Pei-gui,ONGOR B T.Environmental impact assessment using FORM and groundwater system reliability concept:case study Jining,China[J].Environmental Geology,2008,55(3):661-668.

[14]王海龙,余新晓,武思宏,等.SWAT模型灵敏度分析模块在黄土高原典型流域的应用[J].北京林业大学学报,2007,29(增刊2):238-242.(WANG Hai-long,YUXin-xiao,WU Si-hong,et al.Application of sensitivity analysis module of SWATmodel in typical watershed of the Loess Plateau[J].Journal of Beijing Forestry University,2007,29(S2):238-242.(in Chinese))