X线相干散射图像环圆心准确定位的内相关算法
2010-10-09刘太辉刘景鑫李敬筠宋建中
刘太辉,刘景鑫,李敬筠,宋建中
1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130013;2.北华大学 计算机学院,吉林 吉林132031;3.吉林大学中日联谊医院信息中心,吉林 长春 130033
X线相干散射图像环圆心准确定位的内相关算法
刘太辉1,2,刘景鑫3,李敬筠3,宋建中1
1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130013;2.北华大学 计算机学院,吉林 吉林132031;3.吉林大学中日联谊医院信息中心,吉林 长春 130033
X射线相干散射成像分析中,能量的分布为一系列同心圆环。准确地确定圆心是精确提取能量谱线的关键。本文采用K均值聚类结合形态学滤波确定内环区域,使用形心法近似确定圆心,对圆心使用标准差内相关运算逼近标准圆心。实验结果证明,该算法实用、有效。
X线;相干散射;能量分布;K均值聚类;形态学;内相关
专栏——医学成像新技术的研究与应用
编者按:医学影像学科是医院发展及医院收入的重要支柱,与临床医学工程学科有着极其密切的联系。医学影像设备的良好应用需要临床工程师与医疗、技术和护理等多方面人员的密切合作。加强医学影像的质量控制,提高辐射防护手段和水平,开发现有医学影像设备的新功能,开展新设备、新技术的应用和推广,进而提高全院医疗设备的应用水平、利用率特别是设备功能利用率,是我们临床医学工程人员的重要工作内容。

栏目主编:刘景鑫
吉林大学中日联谊医院信息中心主任,吉林省医学影像工程技术研究中心主任,吉林省医学影像质量控制中心副主任,中华医学会医学工程学分会常委,《中国医疗设备》常务编委。教授,硕士生导师,主持国家自然科学基金及省市等多项科研课题。
邮箱: liujingxin@126.com
医学X射线相干散射技术的应用研究是近些年在国际上兴起的一种新的医用病理和物质成分分析技术,可以应用于病理分析、疾病的早期诊断和辅助治疗等方面。目前,国际上在医学相干散射研究上进行了多种形式的研究工作。Puumalainen 等人利用求X射线的相干散射与Compton散射的比率的方式,分析在样品中骨骼矿物质成份的平均电荷密度起伏,用来确定骨骼矿物质密度[1]。骨矿含量(BMC)的测定采用的是单纯的测量相干散射截面与空间角之间的关系[2]。Westmore等人也进行了相干散射成像及物质成份之间关系的研究,通过对不同的单一物质进行成像,可以获得不同空间分布的对称圆环图像[3]。
以临床影像设备成像的方式进行相干散射研究,是临床研究的较好途径。能量分布曲线(能谱)可以准确地反映散射线的空间特征,因此,准确地提取图像的能谱曲线,是相干散射成像技术研究的一个关键环节。相干散射图像具有噪声影响严重、图像分布弥散、没有确定的边界、内部信息互相混叠不易提取的问题。本文综合多种图像处理技术,提出自相关优化方法,准确确定图像环的圆心,为提取图像能量谱提供支持。
1 X射线相干散射图像特点
如图1所示,在样品图中,目标是黑色弥散状的圆环分布,其没有确定的边界。内部的不规则白色区是射线阻挡器的伪影,形状不规则,与圆环不共心。在外标定环(非图像内容)外,还有一些弥散的暗区,分布不具有对称性。同时,通过直方图可见,灰度的分布不具有明显的分类特征,通过直方图进行分割不可行。因此,目标圆环的圆心只能够通过内标定环以内的区域进行标定。
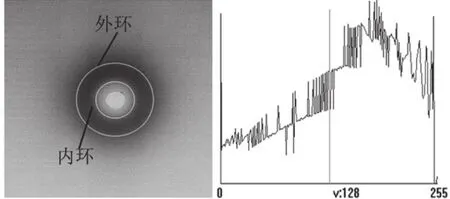
图 1 散射图像及其直方图
2 近似圆心算法
2.1 K均值聚类结合形态学滤波的图像二值化
K均值聚类的基本含义,对于给定的一组数据(x1,x2,x3……xn),如果每一个数据都是一个d维的实向量,则K均值聚类就是把n个数据分割为k组,(k 这里ui是集合Si的均值。这里以图像的灰度值作为分类的依据,即 在此,K均值聚类的目标是有效地划分目标区和背景区。对于散射图像而言,由于噪声的强度与有效值的强度非常接近,而且其分布的灰度范围很窄,所以聚类数K不宜选择过大, 3≤K≤10。重置聚类集内像素点的灰度值,实现二值化: 经过聚类分割后的图像,背景中散落着噪声,圆环的边界模糊不清,目标圆环的内部也散落着白色的背景点。仔细分析背景和目标圆环的图像特征后,背景中的噪声点的分布杂散,没有区域性,而圆环内的背景散落点稀少,不影响圆环的区域特征。这种分布特点恰好可以使用形态学滤波方法进行进一步的平滑处理。 选用3×3滤波器[6] 首先进行一次膨胀运算,加强圆环的区域性,然后进行连续多次的腐蚀操作,剪除背景中的噪声点。 2.2 正交能量投影及形心计算 二值化的图像,需要准确判别环内区域的分布和大小,采用一般的梯度边缘提取算法繁琐而且结果不准确。这里提出基于正交能量投影的算法。 首先,沿着图像的x轴方向和y轴方向,分别作图像的横向和纵向的投影。投影的结果为该方向上单一行(列)内像素点能量的累积。由于图像本身是一个正交的平面,因此投影后的能量累积在特定坐标方向上满足图像分辨率的要求,而且任意的两个x、y方向上独立累积能量所在的坐标位置恰好唯一标定一个图像空间的像素点。 设图像为P={p1,p2,……pmxn}(m,n)∈N,m、n分别为坐标x、y轴方向的图像分辨率。每一个数据pi是二维空间中的一个标量p(m,n)。Em={e1,e2,……en}n∈N, Em为沿着m方向上能量投影集合,同理,En={e1,e2,……em}m∈N 为n方向上的能量投影集合。其中: 投影后的曲线中有明显的波谷存在,波谷是该投影方向上圆环的能量导致的,也就是在两个波谷之间的区域是圆环的内部区域。求得两条谱线上波谷之间区域的中点位置(xc,yc),其对应的图像像素必在圆环内部区域上。以这个点为起始点进行区域增长处理,可以获得圆环内部区域的准确分布,进而对这个区域使用形心算法,提取其形心。这个形心就是圆环的近似圆心。 图 2 求得的形心 相干散射图像在理论上成像圆环完全共心,因此能否准确地确定圆心的位置,是进一步分析的关键。 图像中,根据前面的分析可以知道,除在过圆心的水平轴(x)和垂直轴(y)上的像素点可以被明确地确定为某一个圆环上的点以外,其他的像素点都是通过欧几里德距离计算后,近似归类为某一个圆环。由于在成像探测器对空间中x射线的分布进行成像的量化过程中,成像的结果受空间中的噪声、成像探测器量化误差和采样算法的计算误差的综合影响,只有过圆心的坐标轴上的点相对准确地反映图像对x射线能量分布。 假定当前的圆心为理想圆心,那么当前圆心对应的圆环上的像素分布一定具有强相关性,这种相关是环内像素间的相关,称作内相关性,即像素点的灰度分布在一个相对比较均匀的范围内。而当圆心离开理想圆心位置的时候,由于空间射线分布的高斯特性,新的圆环上的像素点之间的相关性将减低。偏心越严重减低的程度越大。如图3所示,假设理想圆心的位置为xc、yc。圆心向下偏移(xc+3、yc-2)时,所有当前圆心对应的圆环上的点全部改变,相关性会大大降低。 上面的形心方法获得的圆心是一个偏离理想圆心的结果,通过上面相关性分析,可以通过相关性计算使圆心逐渐逼近理想圆心。 图 3 图像中的圆形分布示意图 3.1 相关性测度 样品点是可以准确代表能量分布的像素点。通过前面的分析,在图像中圆环的选取只能够以像素单位进行。无疑以理想圆心为原点的笛卡尔坐标系是分析的标准坐标系,那么x轴和y轴上的像素点就是圆环的标称点,这些点也最适合作为样品点。其他的圆环上的点都具有不同的近似性,不适合作为样品点使用 。 同一个圆环上的样品点的灰度值分布,理想的情况下,应该在一个标准值(平均值)附近摆动,相互间灰度差值很小。这种特性恰好符合标准偏差的理论特征。 那么样品点的标准偏差就可以作为同心圆环上样品点之间灰度分布均匀性的测度。 计算过程中,样品点选择为每一个圆环上以圆心为原点的笛卡尔坐标系中,x轴上圆心对称的两个点,y轴上圆心对称的两个点,总计4个像素点。样品圆环选定为进入有效能量分布区中距离圆心30~60像素距离的一组圆环。 每一个样品圆环上的样品点之间(圆心为理论圆心)具有强相关性,它们的分布标准偏差应该最小(分布在均值附近的很小的范围内)。由于单一的圆环的测度不能够规避掉奇异点的影响,因此可以选择多个圆环作为样品圆环,这里选取为40个样品环。在每一个样品环都计算出标准偏差后,对组标准偏差求均值,作为当前的圆心偏离理想圆心的测度。如果计算过程中,出现2个以上的圆心测度值相等的情况,则以这些样品点作为新的样品圆心,增加或减小样品环的数量,重新计算每个样品圆心的测度,直至没有相同取值存在为止。 3.2 标准偏差 设当前圆心对应的Gi={g1,g2,……,gn}n∈N是第i个圆环上的样品点的集合,那么:样品点的均值为 此组样品点的标准差为: 那么样品圆环组的标准偏差集为{δ1,δ2,δ3,……,δi} i ∈N,则当前圆心的标准差测度为: 3.3 计算方法 标准的圆心必然在图像的内环以内,根据文献资料[7,8]X射线前向小角度相干散射的成像角度在5~10°之间。因此,以成像距离(源到探测器)40cm计算,探测器尺寸(43cm×35cm)高x宽,成像板分辨率(2688×2208)像素。每一个像素点的空间角为0.0219°,那么有效的区域在200个像素点以外。极限情况下,形心算法算得的圆心位于距理想圆心100个像素点的位置上的时候,逼近算法可以准确地搜索到理想圆心,这时候搜索范围应该为100个像素点。而近似圆心如果距离理想圆心的距离超过100个像素点,那么搜索有可能进入能量分布区,相关性测度的计算将无法控制,这个圆心结果应归为坏圆心,需要重新计算。 如图4所示,为典型的四个样品的相关计算结果。在对15个样品图片进行算法的实验计算后,可以得到基本的结论:① 形心算法获得的形心不同程度地偏离理想圆心。② 相关强度随着估计圆心偏离理想圆心而减低。③ 理想圆心具有全局域中最小的标准偏差,具有最大的相关强度。这说明上述的相关算法收敛而且有效。 图 4 内相关强度曲线及求精结果 由于没有准确的边界,也没有评价标准的支持,这里只是简单地以目视可以区分的方式显示圆心准确定位的结果,进一步的理论支持将在以后的科研工作中,通过稳定的算法分析进行验证。 图 5 算法仿真比较图像 如图5所示,图像中b为原始图像,a为经过分析后的放大图像。为了对比方便,在图像中,有两对十字交叉线,前面的一对展示的是精确定位后的圆心,对应白色的圆形区域,该圆形是通过圆形算法和图像区域增长算法结合计算的仿真结果。后面被遮挡的十字交叉线是形心算法的估计圆心,对应的圆形区域为灰色,其大部分被遮挡住。可以通过两个区域的叠加看出两个圆心之间的差异,也可以通过十字交叉线展示两种算法的结果的区别。通过目视可以明显区别出精确计算获得的圆心相比较情况下,更加接近于理想圆心(如图6)。 图 6 仿真结果三组对比图 通过算法结果的分析,本论文中的内相关精确圆心计算方法是有效的,不同的仿真结果也证明了精确定位后的圆心相对于近似估计圆心更加接近于理想圆心。这对后期进行相干散射图像中提取和分析相干散射X射线的能量谱线来说是非常关键的。进一步的工作应该对噪声和奇异点对圆环分布的影响进行分析总结,并完善内相关算法,得到稳定、优化的求精算法。 [1] P.Puumalainen, A.Uimarihuhta, E. Alhava,et al.A new photon scattering method for bone mineral density measurements[J]. Radiology,1976,120:723-724. [2] M.Newton,D.W.L.Hukins,G.Harding.Bone composition measured by x-ray scattering[J].Phys.Med.Biol,1992,37: 1339-1347. [3] M.S.Westmore,A.Fenster,I.A.Cunningham.Angulardependent coherent scatter measured with a diagnostic x-ray image intensifier-based imaging system[J].Med.Phys,1996, 23:723-733. [4] Inaba M.,Katoh N.,Imai H.Applications of weighted Voronoi diagrams and randomiza-tion to variance-based k-clustering[C].Proceedings of 10th ACM Symposium on Computational Geometry,1994:332-339. [5] Kanungo T,Mount D.M., Netanyahu N.S.,et al.An efficient k-means clustering algorithm:Analysis and implementation[J]. IEEE Trans. Pattern Analysis and Machine Intelligence,2002,24: 881-892. [6] Pierre Soille.Morphological Image Analysis: Principles and Applications[M].2 ed. Santa Clara: Springer-Verlag Telos,2003. [7] MacKay, David. Information Theory, Inference and Learning Algorithms[M]. Cambridge:Cambridge University Press,2003. [8] Liu taihui, Sun junxi, Liu jingxin.Medical X-ray Coherent Scatter Images Processing based on the MRF Model[J]. Proc of SPIE,2006,6026:1-9. Inner Correlation Algorithm on Determining Ring Center of X-Ray Coherent Scatter Image LIU Tai-hui1,2,LIU Jing-xin3, LI Jingjun3, SONG Jian-zhong1 R814 B 10.3969/j.issn.1674-1633.2010.07.001 1674-1633(2010)07-0001-04 2010-06-21 国家自然科学基金(60372062)。 本文作者:刘太辉,副教授。 刘景鑫,教授,硕士生导师。 作者邮箱: luke_ciom@yahoo.com.cn Abstract:The energy distribution of X-ray coherent scatter images is a series of concentric rings. It is the key step to determine the center of rings accurately. In this paper, the inside region of image was detected by K-mean and mathematical morphology methods. The center was determined with the centroid algorithm. Then the center was recalculated with the standard error inner correlation algorithm to approach the theory circle center. The experiment result shows that the inner correlation algorithm is effective and practical. Key words:X-ray; coherent scatter; energy distribution; K-Mean cluster; mathematical morphology; inner correlation





3 圆心准确定位算法
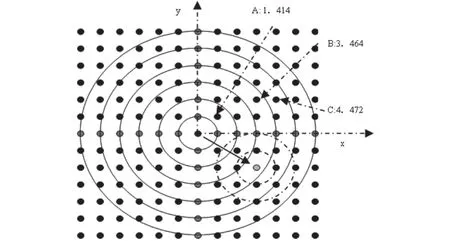



4 实验结果分析



5 结论
1.Changchun Institute of Optics, Fine Mechanics and Physics,Chinese Academy of Sciences, Changchun Jilin 130013, China;2.Beihua University, Computer College,Jilin Jilin 132031, China;3. Information Center,China-Japan Union Hospital of Jilin University, Changchun Jilin 130033, China
