闭口薄壁杆件受碰撞的振动方程求解✳

罗旗帜,徐中山,2,陈玉骥

(1.佛山科学技术学院土木工程与建筑学系,广东佛山 528000;2.华南理工大学土木与交通学院,广东广州 510640)

目前,对结构受碰撞的现象已有不少的理论与实验研究,文献[1-3]分析了结构受冲击的作用,但仅是针对纯弯曲方面,没有考虑结构扭转效应;文献[4-5]进行了薄壁结构的弯扭耦合分析,其采用的方程是根据开口薄壁截面的特征建立的,由于开口和闭口在发生约束扭转的时候,其截面上的剪力流不同[6],因此其采用的动力方程不适合用于闭口截面.本文基于 Timoshenko薄壁梁理论,运用能量原理推出了闭口薄壁结构的动力微分方程,通过积分变换方法求解了闭口薄壁结构受碰撞的动力方程.

1 微分方程的建立

基于乌曼斯基闭口薄壁梁约束扭转理论,截面上任意一点的位移都可通过杆件轴线的基本位移来描

述.设杆件为等截面的直杆,O为截面形心,S为截面的剪切中心,其截面任意一点的位移函数可以表示为

式中:坐标系的原点选在截面的形心上,坐标轴与截面的惯性主轴重合;v s(x)和 w s(x)为截面剪切中心的横向位移;u(x)为截面轴向的平均位移;f(x)为翘曲函数;θ(x)为截面的扭转角;h v(x),h w(x)为截面剪切中心的弯曲转角;总位移 v s(x),w s(x)包括弯曲位移与剪切变形;z s和 y s是剪切中心的坐标;w(y,z)是基于形心的圣维南扭转函数;w s(y,z)为基于剪切中心的圣维南扭转函数,其可退化为横截面的扇性坐标,它满足关系式k s=k-z s y+y s z.

通过建立结构的动能、势能和外力功的能量方程,根据哈密尔顿原理(Hamilton)对能量方程进行变分,整理得微分方程为如下形式

上述方程为 Timoshenko闭口薄壁杆件的动力方程,其中式 (2)是独立的,式(3),(4)和(5)组成了Timoshenko薄壁梁双向弯曲扭转耦合动力方程.Isk为横截面的主扇性惯性矩;J p为截面的方向惯性矩;I k为截面自由扭转惯性矩.Ay和 Az分别为 y方向和 z方向的等效剪切面积,当 Ay→∞,Az→∞ 时,便退化成为 Bernoulli-Euler薄壁梁的弯扭耦合动力方程;当 y s→0,z s→0时,便退化成为截面对称的结构动力方程,如下所示.

假设结构是线弹性的,在没有外力影响的情况下,节点两侧的位移 v s,转角h,弯矩 M,剪力 Q,扭转角θ,翘曲函数 f,双力矩 B,扭矩 L是连续的.自由边界时,M=Q=L=B=0;固定边界时,vs=h=θ=f=0;简支边界时 ,h′=v s= θ=B=0.

结构位移、转角和扭转角等各个参数初始时刻均为零.

质量为 m的质量块以 y方向速度 v撞击梁,将梁分为 n个单元,假设撞击位置为第 i个节点位置,撞击时物体和节点的接触用柔度系数为 f柔的弹簧模拟,其接触平衡条件为(u(t)为撞击物的位移;s为撞击点距形心距离)

2 微分方程的求解

本文针对截面为对称形式的结构动力微分方程进行求解,只考虑撞击方向的横向振动和扭转振动,对式 (7)和 (9)进行 Laplace积分变换,可得如下形式

由此

式中:n1,n2为式 (10a)的特征方程的根;n3,n4为式 (10b)的特征方程的根;c1～ c8为待定系数.

建立结构整体刚度矩阵,代入相应的边界条件、连续条件和碰撞接触平衡条件后,得到各个参数在频域内的解,最后通过 Laplace逆变换的方法,得到各个参数在时域内的解.

3 算例分析

质量为 M的物体以速度 v横向撞击悬臂闭口薄壁梁,用柔度为 f的弹簧模拟物体和梁的接触变形,如图1和图2所示.梁的密度为 7.8×10-6kg/mm3,弹性模量为 210 GPa,梁长 2 000 mm,梁的截面形式如图2所示.撞击物的质量为 100 kg,撞击速度为 3 m/s,柔度系数为 0.2 m/MN.截面以剪切中心为零点,碰撞点距剪切中心的横向距离即偏心距为 75 mm,o为截面剪切中心.

图1 撞击示意图Fig.1 Mechanical model of impact

图2 结构横截面图(mm)Fig.2 Diagram of cross section

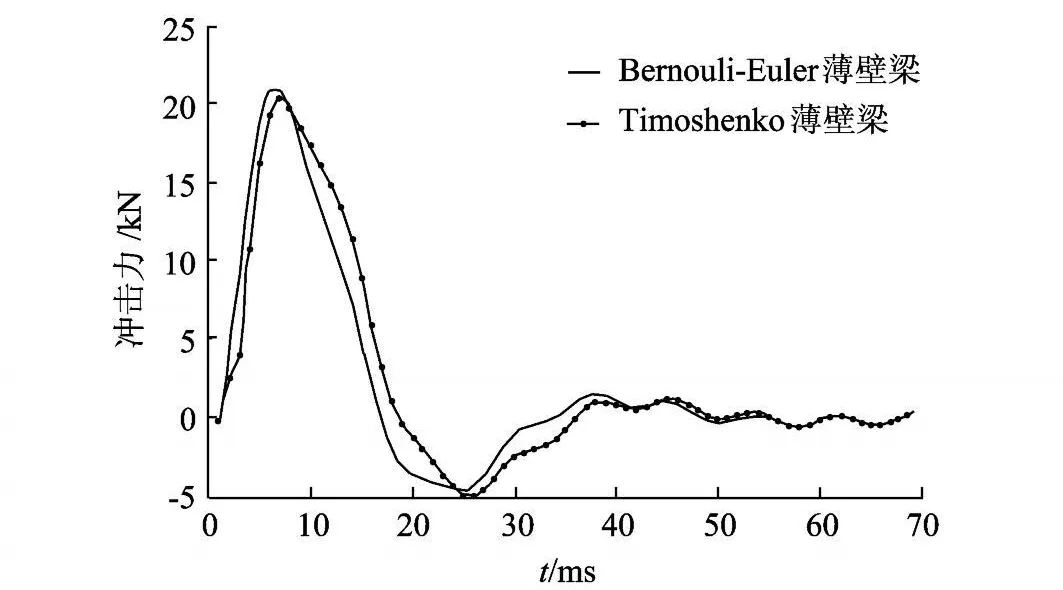
图3 冲击力示意图Fig.3 Diagram of impact force

经计算得到冲击力(图3)、撞击点处剪切中心的 y方向位移 v s(图4)和扭转角的最大动力响应 (图5).图3显示 Timoshenko闭口薄壁杆件受的冲击力与 Bernoulli-Euler闭口薄壁杆件受的冲击力相差 2.70%,说明考虑剪切变形对结构所受冲击力的影响不大.图4,图 5为 Timoshenko闭口薄壁杆件与Bernoulli-Euler闭口薄壁杆件的冲击点处的位移和扭转角的动力响应最大时刻的示意图.从图4可以看出,考虑剪切变形后的梁中点处的最大位移为 -6.983 1 mm,Bernoulli-Euler梁的位移值为 -5.867 2 mm,两者相差15.98%,这说明考虑剪切变形对位移的贡献较大.而图5显示,考虑剪切变形之后,梁冲击点处的扭转角的最大动力响应值相差为 0.24%,说明剪切变形对扭转角的影响比较小.

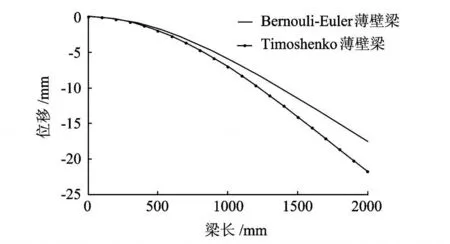
图4 撞击点处 v s的动力响应Fig.4 Dynamic response of v s displacement at theimpact site

图5 撞击点处扭转角的动力响应Fig.5 Dynamic responseof torsion angleθ at theimpacesite

4 结 论

1)基于 Timoshenko薄壁梁理论,运用能量原理建立了薄壁结构受碰撞的弯扭耦合动力方程,该公式经退化后可得到 Bernoulli-Euler梁动力方程,说明本文方法具有普遍性;

2)在结构受碰撞的过程中考虑剪切变形对冲击力和扭转角的影响较小,但对横向位移的影响比较显著,所以在计算位移时要考虑剪切变形,但在计算冲击力和扭转时可以忽略剪切变形的影响.

[1]Lam K Y,Sathiyamoorthy T S.Reponse of composite beam under low-velocity impact of multiple masses[J].Compsite Structures,1999,44:205-220.

[2]Yang JL,Xi F.Experimental and theoretical study of free-free beam subjected to impact at any cross-section along its span[J].International Journal of Impact Engineering,2003,28:761-781.

[3]黄剑敏,任文敏.弹性杆与结构接触冲击的冲击力计算研究[J].应用力学学报,1996,13(3):115-118.Huang Jianmin,Ren Wenmin.Impact force calculative investigation of contact impact between elastic bar and structure[J].Chinese Journal of Applied Mechanics,1996,13(3):115-118.(in Chinese)

[4]鲍四元,邓子辰.弹性撞击作用下弯扭耦合梁的动力响应[J].应用力学学报,2008,25(3):415-420.Bao Siyuan,Deng Zichen.Dynamic response of bending-torsion coupled beam under elastic impact[J].Chinese Journal of Applied Mechanics,2008,25(3):415-420.(in Chinese)

[5]李俊,金咸定,何东明.确定性荷载作用下 Timoshenko薄壁梁的弯扭耦合动力响应[J].力学季刊,2002,23(3):380-385.Li Jun,Jin Xianding,He Dongming.Dynamic response of bending-torsion coupled timoshenko thin-walled beam under deterministic loads[J].Chinese Quarterly of Mechanics,2002,23(3):380-385.(in Chinese)

[6]包世华,周坚.薄壁杆件结构力学[M].北京:中国建筑工业出版社,2006.