圆柱钢管混凝土梁柱节点性能分析
2010-09-29宋彬彬甘文举
宋彬彬,甘文举
(湖南理工学院 土木建筑工程学院, 湖南 岳阳414006)
圆柱钢管混凝土梁柱节点性能分析
宋彬彬,甘文举
(湖南理工学院 土木建筑工程学院, 湖南 岳阳414006)
对圆柱钢管混凝土柱—钢梁节点局部模型进行非线性分析,讨论了节点的应力传递机理,钢管壁变形规律,并与试验结果比较,考察有限元分析对实验过程模拟的可行性.
圆钢管混凝土;梁柱节点;有限元;非线性分析
引言
本文采用通用有限元分析软件 ANSYS对无横隔板及有横隔板加强的圆钢管混凝土柱—钢梁节点局部模型试件进行加载过程模拟,分析对象均为双向试件:无横隔板加强的一方向受拉、另一方向受压试件BMN1及有贯通横隔板加强的一方向受拉、另一方向受压试件BMD1.为节约计算资源,依据试件对称性,取试件的计算,各边界面处的约束条件按对称面要求施加,拉压荷载按相应比例增减.试验结果则建立在对实际工程中的钢管混凝土框架结构梁柱节点进行简化所采取的节点局部模型基础上,其中柱为圆形钢管混凝土柱,梁为H型钢梁,在H型钢梁的受压翼缘处,由于填充混凝土可以分担很大一部分压力,节点受压区总的强度要高于受拉区,为了简化起见,仅取受拉翼缘部分作为分析对象.
1 单元类型
由于柱钢管管壁较厚,为了能够比较准确地模拟实际情况,钢管、钢梁翼缘、填充混凝土均采用八节点弹塑性实体单元 SOLID45,分析中考虑梁翼缘与柱钢管焊缝的影响,也采用 SOLID45建模;为考虑混凝土与钢管管壁之间在加载过程中的接触与脱离,采用三维面—面接触单元 CONTA174和 TARGE170;试件上不施加轴向力,对钢管与混凝土之间的粘结与摩擦可不考虑.
2 材料参数
各材料参数依据材料试验的实测数据简化得到,钢梁翼缘和钢管柱材料的应力—应变关系分别为多线性模型,钢材和焊缝材料的屈服准则采用Von Mises准则,流动准则采用相关流动准则,由于计算仅限于初始各向同性的小应变分析,强化准则采用的是随动强化,包含包辛格效应;混凝土应力—应变关系为双线性模型,由于在三向受压的情况下混凝土表现出良好的塑性,因此建模时不考虑混凝土的破坏,取泊松比为0.167,屈服准则按Drucker-Prager准则考虑,粘聚力等材料参数见表1.

表1 填充混凝土的材料参数
3 有限元模型
各试件的有限元模型如图1所示,其具体尺寸均依据实测数据确定.为保证计算精度,全部采用六面体单元,在梁翼缘与柱钢管焊缝连接处应力梯度较大,对其附近的钢材与填充混凝土网格适当加密.试件BMN1、BMD1的FEM模型节点总数分别为27757、37536,实体单元总数分别为19245、29203,接触单元总数分别为12438、6883.

图1 有限元模型
4 有限元分析结果及试验结果
4.1 梁翼缘应变分布
各试件梁翼缘应变分布如图2所示,图2给出了试验结果与有限元分析结果(有限元结果指节点在最大抗拉强度时的梁翼缘断面纵向应变分布),可见无横隔板节点梁翼缘应变在受拉侧中心部分比断面边缘部分集中,沿断面呈马鞍形分布,峰值对称出现在距两侧边缘约梁宽处,断面边缘则出现了较小的压应变,梁翼缘断面受力很不均匀,在节点最大抗拉强度时未到屈服应变(0.161%),梁处于弹性状态;而贯通横隔板加强节点受拉侧梁翼缘应变断面边缘比中心部分集中,应变分布呈波峰状,峰值对称出现在两侧边缘处,梁翼缘断面中心部分拉应变比较小,边缘部分应变则较大,梁翼缘断面受力相对较均匀;在节点最大抗拉强度时整个断面已达到屈服应变 0.161%,钢梁已处于塑性状态,两种情况下受压侧对受拉侧结果影响均不大.
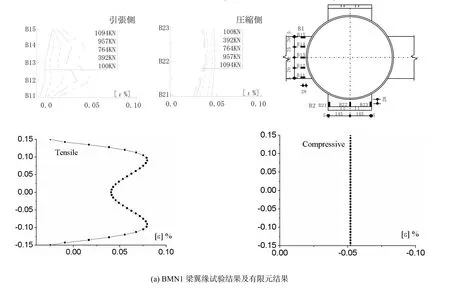

图2 各试件梁翼缘应变结果比较
试验构件的加载方法为在X方向梁翼缘施加单调增加的拉伸荷载Px,同时对Y方向梁翼缘施加单调增加的压缩荷载Py,在加载的过程中始终保持Py=−Px.在双向加载达到破坏后,保持X方向的受力不变,继续沿y方向施加压缩荷载直至构件完全破坏.在试件的下列相应位置处布置应变片以测定其应变数据:梁翼缘断面方向处、梁柱节点附近的柱钢管管壁处.试件BMN1的受拉梁翼缘断面中心部分应变比断面边缘部分应变集中,而受压侧梁翼缘断面边缘部分由于填充混凝土抗压能力的原因出现应变集中;试件BMD1在梁受拉侧以及受压侧的应变都是梁翼缘断面边缘部分比断面中心部分更早达到屈服,并且在梁受拉侧最大拉应变为5.0% ,而受压侧梁翼缘断面边缘部分同样出现了应变集中.由图2可见有限元分析结果与试验结果对应良好.
4.2 柱钢管管壁应变分布
各试件柱钢管管壁应变分布试验结果与有限元结果如图3所示,双向受力试件BMN1与BMD1均给出受拉侧应变结果,有限元结果是节点最大抗拉强度时柱钢管管壁外表面的应变分布.可见在梁翼缘中心线及翼缘边缘处,试件节点受拉侧的柱钢管管壁沿管轴方向V1、V2的表面应变分布在焊脚处呈正弯曲的拉应变,离开焊脚一定距离处渐变为负弯曲的压应变,而梁翼缘边缘处沿柱钢管管周方向H2的表面应变分布总体上表现为拉应变,在接近梁翼缘处达到最大值,有、无横隔板对柱钢管壁应变影响不大.
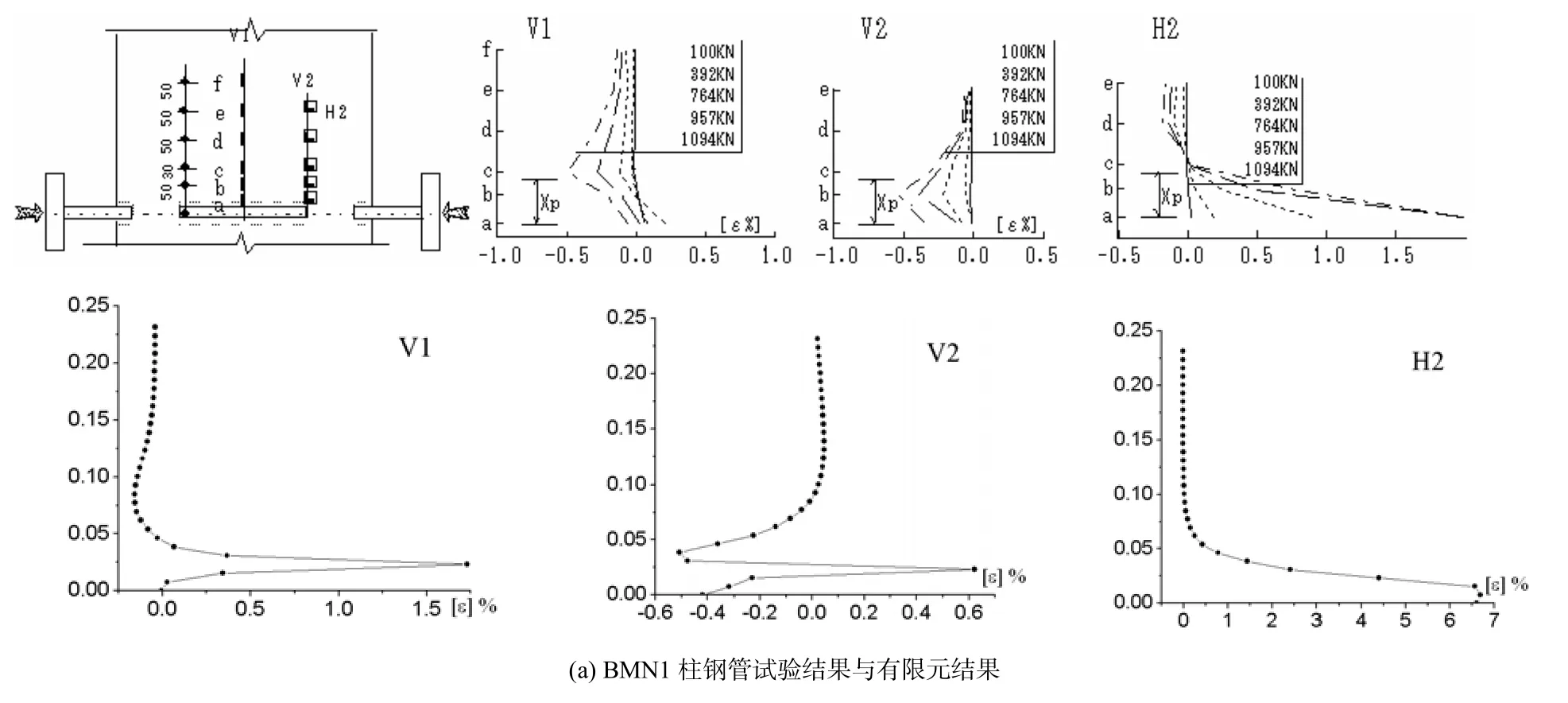
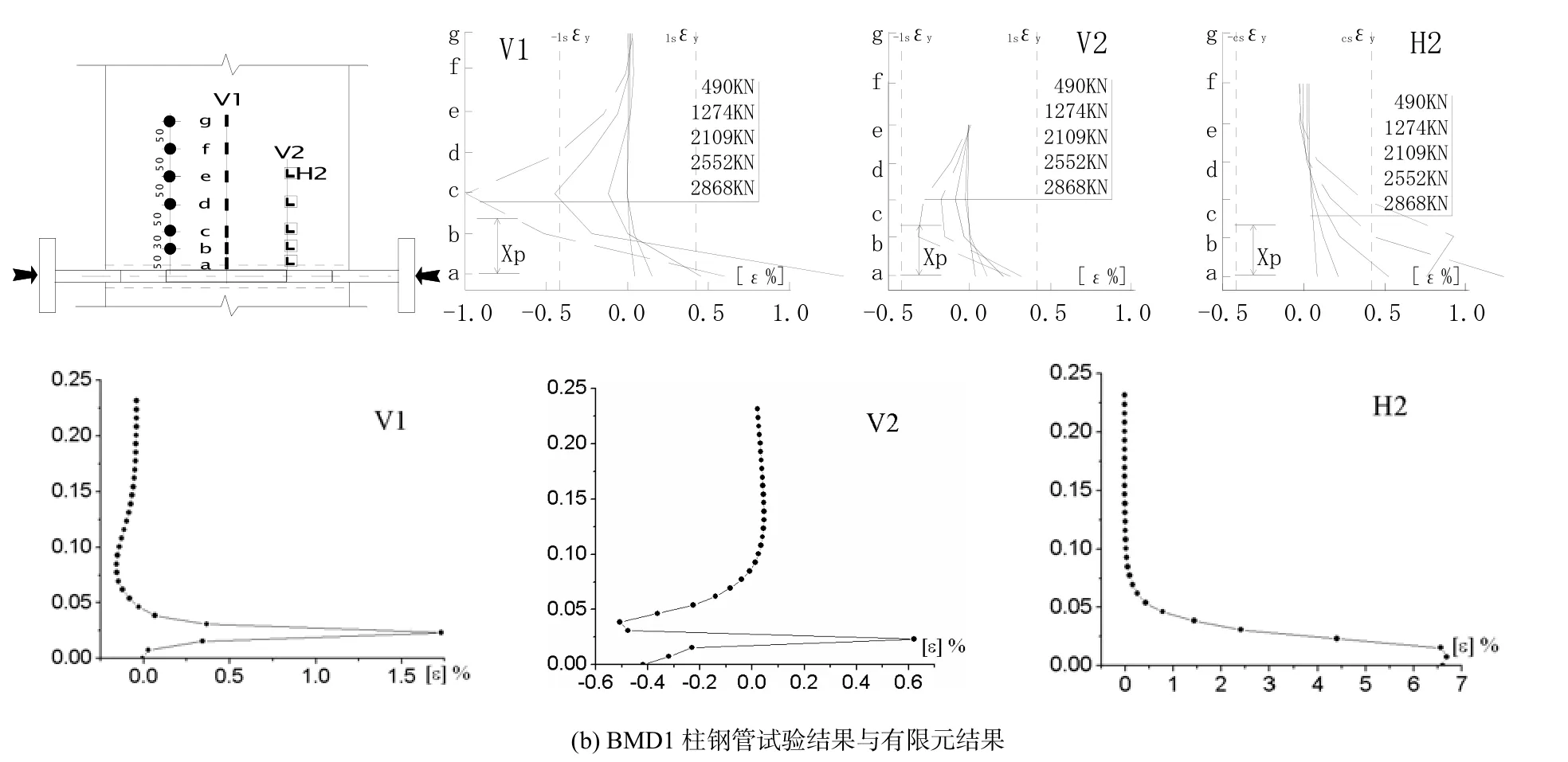
图3 各试件柱钢管管壁应变结果比较
在实验结果中,试件 BMN1试件受拉侧的柱钢管管壁在梁翼缘中心线处及在梁翼缘边缘位置处沿管轴方向的表面应变(如图中 V1和 V2所示)均在焊脚处呈正弯曲的拉应变,在离开焊脚一定距离处呈负弯曲的压应变.在梁翼缘边缘位置处沿管周方向的柱钢管管壁表面应变分布(如图中H2所示)在接近梁翼缘处呈现出较大的拉应变.试件BMD1在受拉侧梁翼缘中心线管轴方向V1焊脚处呈正弯曲的拉应变,离开焊脚一定距离处呈负弯曲的压应变,而在受拉侧梁翼缘边缘部分管轴方向V2位置处,钢管沿管周方向比沿管轴方向更先达到屈服;受拉侧的梁翼缘边缘位置沿管周方向H2的柱钢管管壁表面应变在接近贯通横隔板处呈现出较大的拉应变.试件BMN1与试件BMD1的柱钢管管壁表面应变分布比较一致,并且试验结果与有限元结果对应良好.
在试验中,焊缝附近区域钢管壁应变无法测量,而有限元结果给出了这一范围内柱钢管壁应变分布情况.各应变图中在纵坐标为 0~25mm 范围内是焊缝区域,在此范围内应变片无法布置,从而没有试验结果,但从有限元分析的结果则可以观察到此区域范围内的应变分布情况:在焊缝连接处应力集中、形状也不规则,受力情况相当复杂,不仅应变的绝对值很大,应变的变化也很剧烈,在整个梁翼缘范围内是最先屈服并且达到拉应变峰值的;压应变的峰值则相对较小,而且出现的位置和离开梁翼缘断面中心的距离有关,在梁翼缘断面中心处离焊缝较远,而在梁翼缘边缘位置处则很接近焊缝.
5 结 论
本文用有限元程序对无横隔板和有贯通横隔板加强的圆柱钢管混凝土柱—钢梁节点局部模型进行有限元分析并与试验结果从梁翼缘应变、圆柱钢管管壁应变两个方面进行比较,分析对象取BMN1、BMD1两个双向试件,据此讨论节点的屈服机理,分析了两种节点的梁翼缘及柱钢管壁应变分布规律.由此可知,有限元模拟试验有其可行性、合理性、适用性,可将之做为试验分析的有效补充手段.从数值分析的角度出发,其精确度和正确性可以得到保证,并且可以分析试验中无法测出其应变的复杂部位(如焊缝处),对其受力性能做出定性分析.
[1]任启辉.ANSYS7.0工程分析实例详解[M].北京:人民邮电出版社,2003
[2]叶先磊,史亚杰.ANSYS工程分析软件应用实例[M].北京:清华大学出版社,2003
Nonlinear Finite Element Analysis of Connection Between Steel Beam and Concrete-Filled Circular Column Tube
SONG Bin-bin,GAN Wen-ju
(College of Civil Engineering and Architecture,Hunan Institute of Science and Technology,Yueyang 414006,China)
Based on nonlinear finite element method and FEM analysis,the connection between steel beam flange and concrete-filled circular column tube was discussed.Comparing with the results of experiment,the feasibility of experimental process simulation based on nonlinear analysis was investigated.
concrete filled tube;beam-to-column connection;finite element;nonlinear analysis
TU398
A
1672-5298(2010)04-0072-04
2010-09-07
湖南省教育厅科研基金项目(09C475)
宋彬彬(1976− ),女,湖南岳阳人,湖南理工学院土木建筑工程学院讲师.主要研究方向:结构工程
