一种用于等值线数据重建目标三维模型的算法
2010-09-28李玉潮黄培之
李玉潮,黄培之,陈 玲
(1.郑州测绘学校,河南郑州 450005;2.深圳大学,广东深圳 518060; 3.深圳市腾讯计算机系统有限公司,广东深圳 518057)
一种用于等值线数据重建目标三维模型的算法
李玉潮1,黄培之2,陈 玲3
(1.郑州测绘学校,河南郑州 450005;2.深圳大学,广东深圳 518060; 3.深圳市腾讯计算机系统有限公司,广东深圳 518057)
利用等值线数据重建目标三维模型在实际工程中有着广泛的应用。在研究现有的利用等值线数据重建目标三维模型的方法后,提出一种基于等值线图形形状相似性变换的三维表面重建方法。试验结果表明,该方法比现有的利用等值线数据重建目标三维模型的方法能更好地实现三维表面重建。
等值线;三维模型;相似性;势能场
一、引 言
利用等值线数据重建目标三维模型是计算机图形学的一个研究内容,它在实际工程中有着广泛的应用。如医学图像处理中利用人体器官的 CT图像轮廓线重建该器官的三维模型,以帮助诊断该器官的病变;在测绘工程中利用等高线数据建立数字地面模型(DEM),以帮助规划、设计、军事等部门解决各自领域的问题。
传统的利用等值线数据重建目标三维模型的方法主要包括数据点的采集和内插点的获取两个内容。前者以分析等值线形态变化获取能够描述该等值线形状的特征点作为采样点数据;后者用与内插点相邻近的采样点建立局部函数,获得描述目标表面的局部函数,从而得到内插点数据[1]。分析现有三维目标表面重建内插点获取的算法可以知道,这些内插算法在获取内插点时大多是只采用与该点相邻近的少数采样点进行内插计算,而没有顾及采样点数据的整体特性和内在联系。这样所获得的内插点只能够顾及地形变化的局部规律,而忽略了地形变化的整体规律。它使得重建后的目标三维模型的质量和准确性难以得到保障,甚至有时会出现错误[2]。因此,需要对利用等值线数据重建目标三维模型这一问题进行深入研究。
二、利用等值线数据重建目标三维模型的方法
常用的利用等值线数据重建目标三维模型的方法有不规则三角网方法 (triangulated irregular network,T IN)和局部函数法[1]。
T IN是根据原始等值线上的采样点构建不规则三角网,其实质是将相邻等值线上相近的三点构成最佳三角形,使每个数据点都成为三角形顶点。这样就可以用这些三角形片面拟合相邻等值线之间的三维表面。相邻等值线之间的任意一点 P(Xp, Yp,Zp)的内插值可由式 (1)根据该点所在的三角形片面的 3个三角形顶点的坐标 (Xi,Yi,Zi,i=1,2, 3)计算获得。
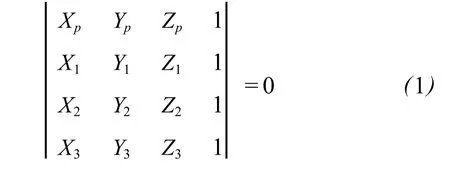
局部函数法是以内插点为中心,用与其相邻的n(n大于局部函数中的待定参数的个数)个采样点拟合一个局部函数,采用最小二乘法原理解求该局部函数的待定参数,然后根据这个局部函数解算出内插点的内插值。移动曲面法是一种常用的局部函数法,它通常采用式 (2)描述的二次多项式来拟合一个局部函数。
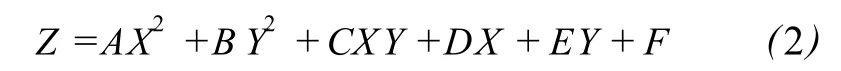
以上两种算法皆为单点解求内插点的内插值,为了提高解求内插点的效率和可靠性,研究人员研究出了整体内插方法[1]。该方法是以规则格网点为内插点,用局部函数建立相邻格网点和该格网点内的采样点之间的数学关系,然后对相邻格网的局部函数进行光滑性约束,建立起相邻局部函数之间的数学关系,最后整体求解出所有内插点 (格网点)的内插值。该方法常用的局部函数有双线性函数(见式 (3))和双三次函数 (见式 (4))。
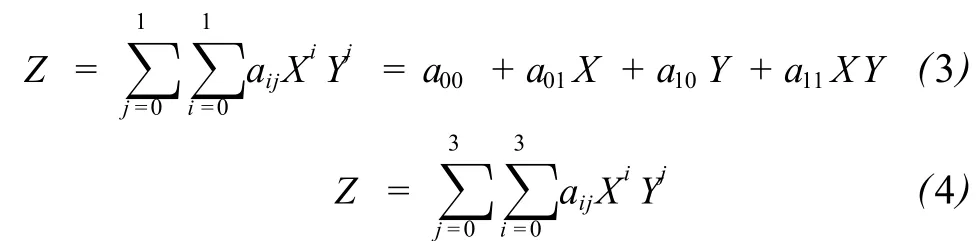
对现有的利用等值线数据获取内插点的算法进行分析可以知道,这些内插算法在获取内插点时大多是只采用与该点相邻近的少数几个采样点进行计算,而没有顾及采样点数据的特性和内在联系。这样所获得的内插点只能够顾及三维表面变化的局部规律,而忽略了三维表面变化的整体规律。它使得重建后的三维表面的质量和准确性难以得到保障,甚至有时会出现错误。
三、基于相邻等值线形状相似性的三维表面重建方法
由于等值线是三维实体目标的外轮廓线与一组平行面的交线的集合,可以证明相邻等值线的形状具有一定的相似性[3]。这种相似性关系与等值线之间的三维表面的变化状况有关,因此它能够间接地反映等值线之间的三维表面的变化状况。现有的利用等值线数据进行三维目标重建的方法在获取内插点时仅仅采用与该内插点较邻近的少数采样点,显然是不合理的。它忽略了相邻等值线间的三维实体目标表面变化的整体规律,这一理论上的缺陷制约了这类算法获取内插点的最终结果的质量和准确性。
为了克服现有的利用等值线数据获取内插点算法的缺陷,建立能够描述相邻等值线形状之间的相似性变化规律的模型具有一定的意义。由物理学原理知道,某些物理场 (重力场、电势能场等)的场强度等值线与产生该物理场的场源形状具有相似性,并且这种相似性随场强度等值线距场源的平面距离的增加 (减少)而单调减少 (或增加)。该种关系反映到场强等值线上就是场强度等值线形状的差异随场强度值的增加 (或减少)而单调减弱(增强)。因此可以借助物理学中的场强度模型来研究分析等值线形状的变化规律[4]。具体方法如下:
设两相邻等值线分别为 c和 c′,若将其视为均匀分布着一定数量电荷的两个带电体,则根据电学知识可以知道,在 c和 c′之间的环形区域可以形成一个电势场。该电势场中任意一点的场强度可由式(5)获得。
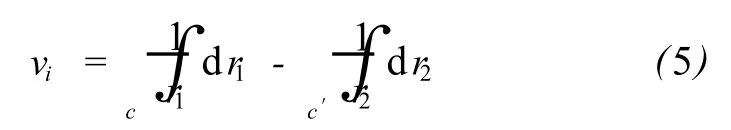
其中,r1、r2分别为电势场中任意一点到场源曲线 c和 c′上点电荷的距离。
分析式 (5)可以知道,由于电势场强度与距场源的距离 r成反比,因此,由式 (5)计算出的电势场强度在距场源的距离 r小于某一阈值 T时,其场强度变化很大;而当距场源距离 r大于该阈值时,其场强度变化较为平缓 (见图 2(c))。显然,直接用电势场强度模型式(5)来模拟目标三维表面变化是不合适的。对电势场强度模型和相邻等值线之间的三维表面变化规律进行研究可以知道,适当地选择式(6)中的随到场源的距离 r而变化的函数 f(r)可以获得与三维实体目标表面变化规律大致相同的场强度模型 (见图 2(d))。
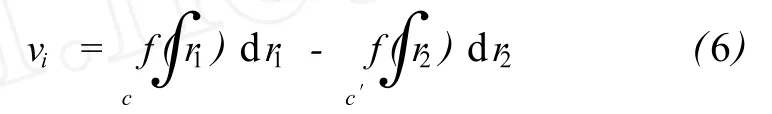
根据上述原理,笔者通过研究得出选择指数函数 f(r)=1/ur(u为常数)可以较好地用来模拟三维实体目标的表面变化规律[3]。
四、试验结果与分析
为了验证和评估本文所述的方法,笔者进行了试验。
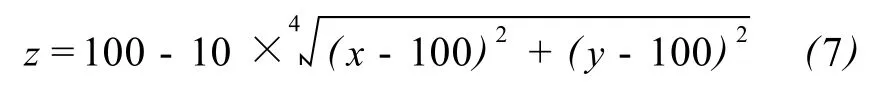
在试验一中,笔者对式 (7)描述的抛物面 (见图 1(a))分别用 z=0、z=50两个水平面截取抛物面得到两条相邻等值线 c′、c(见图 1(b)),其方程为
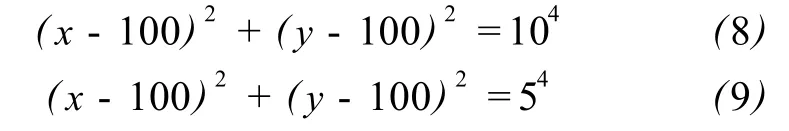
在这两条等值线上各取若干点作为采样点数据进行试验分析,最大试验区域为 200×200(见图 1(b))。
试验一分别用线性内插、三次多项式内插、广义势能场模型、f(r)=1/ur模型 (其中 u=1.03)对图 1(b)所示的等值线数据进行实体目标三维表面重建,图 2是重建结果。用试验结果所得到的目标三维表面数据与由式 (7)计算出的理论值 (见图 1(a))比较可以得到各种方法的误差数据 (见表 1)。从表 1中可以看出用 f(r)=1/ur模型进行三维实体目标表面重建,其中误差、平均误差、最大误差皆为最小。

图1 试验一所用数据

图2 试验一的结果
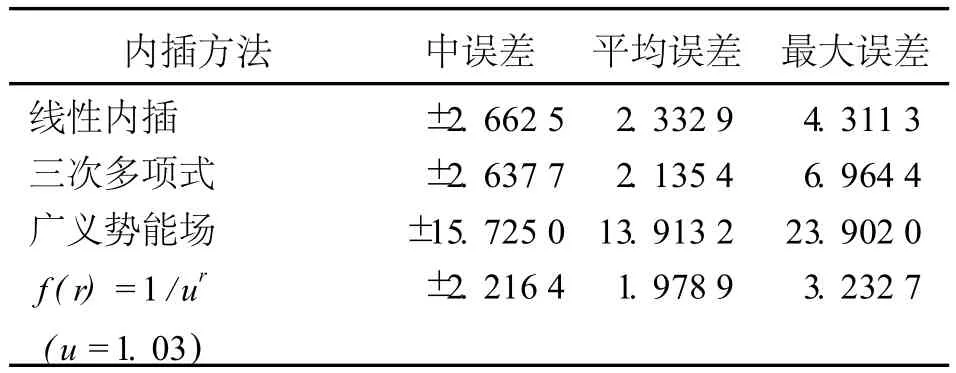
表1 试验一结果统计分析
为了验证 f(r)=1/ur模型的实用性,笔者用两条相邻等值线进行试验 (见图 3),试验结果见图 4。从试验结果图 4可以看出用 f(r)=1/ur模型重建的相邻等高线之间的地形曲面所含地形信息十分丰富,地形细部清楚,能够较好地描述相邻等高线之间的地形变化情况。

图3 试验二所用数据
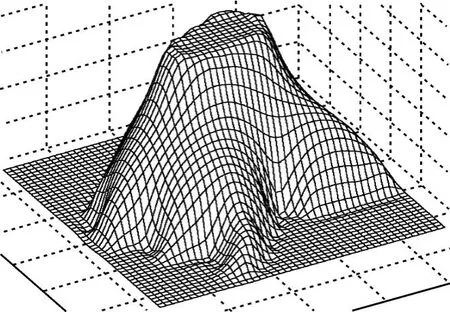
图4 试验二结果
[1] 张祖勋,张剑清.数字摄影测量学[M].武汉:武汉测绘科技大学出版社.1997.
[2] 黄培之.等高线形状变化规律的研究[J],中国图象图形学报,2006,11(1):103-106.
[3] 黄培之.基于等高线特性数据的三维表面重建方法的研究[J].武汉大学学报:信息科学版,2005,30(8):668-672.
[4] LA I POH-CH IN,黄培之.2D几何图形整体内插的一种方法[J].计算机学报,1999,22(2):165-170.
An Algorithm for Three-d imensional Surface Reconstruction from Contour Data
L I Yuchao,HUANG Peizhi,CHEN Ling
0494-0911(2010)08-0015-03
P23
B
2010-07-01
李玉潮(1956—),男,河南南阳人,高级讲师,主要从事摄影测量与遥感、数字制图和地理信息系统方面的教学和研究工作。
