单位四元素法在激光点云坐标转换中的应用
2010-09-28滕志远张爱武
滕志远,张爱武
(首都师范大学资源环境与旅游学院三维信息获取与应用教育部重点实验,北京100048)
单位四元素法在激光点云坐标转换中的应用
滕志远,张爱武
(首都师范大学资源环境与旅游学院三维信息获取与应用教育部重点实验,北京100048)
将点云配准过程中的单位四元素法应用于坐标转换,提出一种在求解坐标转换过程中将旋转矩阵和平移向量转化为求解多元函数极小值的方法,直接解出坐标转换的旋转矩阵和平移向量。与目前常用的一些方法相比,具有适应大旋角、不受平移参数影响、计算简便快速、便于程序实现等优点。最后验证该方法的精度,并用实测数据检验其可行性。
坐标转换;七参数;单位四元素法
一、引 言
随着测量技术的发展,三维激光扫描的应用越来越广泛。三维激光扫描仪受外界环境影响小,能够快速、连续地获取数据,具有精度高、适应性强、应用广泛、操作简便等诸多优点。目前,三维激光扫描技术已在工程测量、地形测量、交通现场勘测、桥梁变形监测、古建筑和文物保护、数字城市等多个领域得到应用,取得了很好的效果[1]。
激光扫描仪获取的数据所采用的坐标系统是它自己定义的局部三维直角坐标系,而不是各种实际中广泛采用的坐标系,如1954北京坐标系[1]。而且在不同的站点,扫描仪的局部坐标系也是不同的。这样既造成各站点的点云需要配准[2],又使其应用范围受到限制。如果能将点云坐标转换为实际中广泛应用的坐标,既能实现点云的配准,又能扩大点云的应用范围。本文提出了一种将三维激光扫描仪的点云数据从其局部坐标系转换到其他三维坐标系的方法。
二、转换模型
传统的三维坐标转换方法,使用的是线性化的布尔沙模型[3]。在该模型中,需要求解3个旋转角度参数,3个平移参数,1个尺度参数,共7个参数[4]。也称为七参数法。转换公式如下


其中XT=[X Y Z]T,为转换后坐标;ΔX=[Δx Δy Δz]T,为平移向量,X=[x y z]T,为待转换坐标;α、β、θ分别为X、Y、Z轴的旋转角度,K为尺度参数。
如果7个参数已知,即可按照布尔莎模型公式,实现坐标的转换。但在实际应用中,这7个参数是未知的,可如果知道3个重合点[5]就可以用最小二乘法拟合出七参数。拟合七参数的过程一般是对旋转矩阵进行线性化后再计算七参数,但这种方法只能针对微小旋转角的情况。当旋转角度较大时,会产生较大的误差,损害坐标转换精度[6]。
为能更精确地求解七参数,科技工作者提出很多方法。如陈宇提出了非线性最小二乘的方法求解七参数,解决了大旋角情况下七参数求解[6]问题;陆珏等提出了基于总体最小二乘的方法求解七参数[7];这些方法都是基于最小二乘拟合的思想,原理比较复杂。
本文借鉴了点云配准中的思想,将配准过程中单位四元素方法应用于坐标转换。
三、单位四元素法
配准的过程是将不同站点点云统一到同一个坐标系下的过程。因而点云配准的过程其实也是点云的三维坐标转换的过程。
单位四元素法的思想[8]如下:
若目标点集A对应于参考点集X,对应点集满足:两个点集中点的个数相等,点集中的点要一一对应。设旋转变换向量为单位四元数

可得到3×3旋转矩阵R(qR)。设平移变换向量为
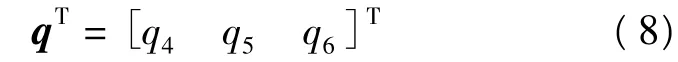
可得完全坐标变换向量q=[qR|qT]。则求对应点集间的最佳坐标变换向量问题可转化为q,即使得函数

最小化的问题。
在单位四元素法中,至少需要知道3对一一对应点的坐标。
算法过程[2]如下:
1)分别求重心:原始点重心为
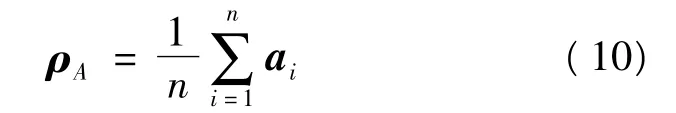
转换后点重心为
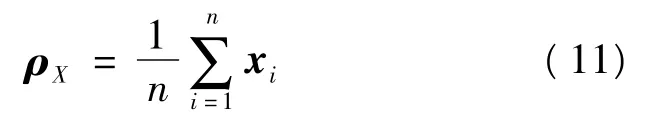
其中,n代表有n对对应点,ai、xi为带有x、y、z坐标的点。
2)构造协方差矩阵为
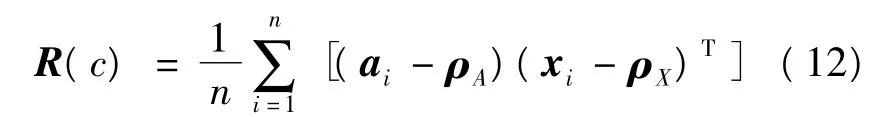
3)构造4×4矩阵为

其中,tr(R(c))是矩阵R(c)的迹;I3是单位3×3单位矩阵;Δ为

其中
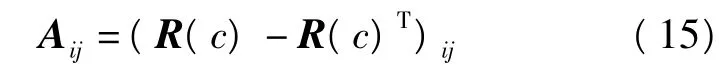
4)计算4×4矩阵R(q)的特征值和特征向量,其中最大特征值对应的特征向量即为单位四元数[q0q1q2q3]T。
5)计算旋转矩阵为

其中,R11=q20+q21-q22-q23;R12=2(q1q2-q0q3);
R13=2(q1q3+q0q2);R21=2(q1q2+q0q3);
R22=q20-q21+q22-q23;R23=2(q2q3-q0q1);
R31=2(q1q3-q0q2);R32=2(q2q3+q0q1);
R33=q20-q21-q22+q23。
6)计算平移矩阵为
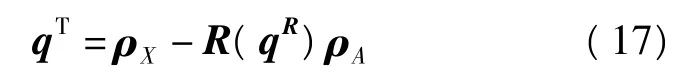
至此,计算出了旋转矩阵和平移向量,即可实现坐标转换。
四、测试试验
本文选取6个点,其中3个点既有在扫描仪下的坐标,又有在转换后坐标系下的坐标。这3个点是用来求旋转矩阵和平移向量的。另外3个点则已知在扫描仪下的坐标。
由于是直角坐标转换,设定尺度参数k=0,1~3号点原始坐标分别为:(32.503,163.608,0.029),(31.534,167.955,-1.164),(25.723,169.838,5.343)。
4~6号点原始坐标分别为:(72.356,163.140,1.948),(65.148,175.564,12.566),(85.720,155.195,20.232)。
表1是模拟测试试验的结果。表1中的理论值是用七参数转换公式,将4~6点坐标和参数代入七参数转换公式算出的值。转换值是4~6号点的原值代入单位四元素法算出的旋转矩阵和平移向量得出的值。此处的旋转矩阵和平移向量是利用1~3号点原坐标值和经七参数转换后的坐标值算出。
如表1所示,在第一组和第二组中,平移向量参数都是确定的,两组数据分别试验了在不同旋角情况下坐标的转换精度。由理论值和转换值的对比可以看出,不论是大旋角还是小旋角,坐标转换的误差都很小,最大的误差也在10-6数量级,可见本文算法在旋角很大的情况下,也有很高的转换精度。
第一组和第三组同样有相同的平移参数,只是三个坐标轴旋角值做了对调。由表中数据可以看出,本文算法对各个坐标轴的旋角大小无特殊要求,不论旋角是大还是小,算法均有很高的转换精度。在第一组和第四组中,有相同旋转参数,不同的平移参数。这种情况下,误差仍然很小,与前面的误差相比没有大的变化,说明平移参数的大小对算法几乎没影响。将第二、三、四组的数据进行对比,在不同的旋角和不同的平移参数下,理论值和转换值的误差依然在10-6数量级。
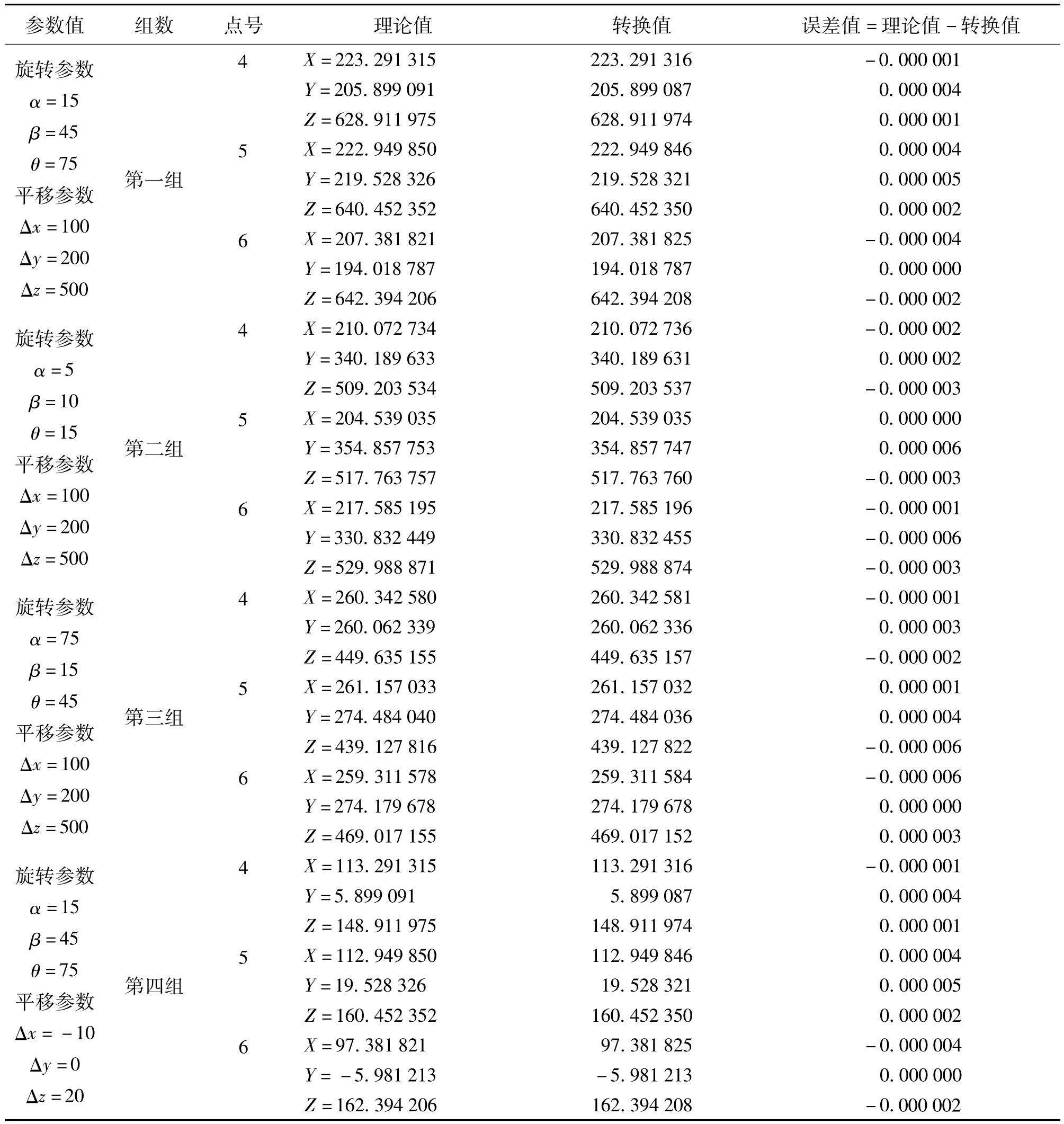
表1 测试试验
综合以上的数据对比可以得出,本文算法在大旋角的情况下依然适用,且保持了很高的精度。旋角的大小和平移向量的大小对算法的精度几乎无影响。
本文的算法编程实现简单易行,运算快速。在CPU为奔腾4,主频为3.0 GHz,内存512 MB的硬件条件下,用VC 6.0编译,实现741 389个点的转换并将结果输出到磁盘上,用时22 s,而实现59 379个的点转换并输出到磁盘仅用时约1 s。
五、实测数据检验
为检测实际效果,我们选取了一组实测数据用来检验算法。实测数据是将一段公路分为两个站点进行扫描。在每一个站点的扫描前,先放置五个靶标。靶标由于反射率较高,在后处理软件中容易识别,并取得该处靶标在扫描仪坐标系下的坐标。每一站扫描完毕,用GPS测出靶标的全局坐标(这里将全局坐标转换为1954北京坐标系)。这样在每站点云数据上,就至少有3对点可用来转换坐标系。
如图1~图2所示的是采用本文的算法转换后的坐标点的图像。图中深灰色的是一站数据,浅灰色的是另一站数据。为了突出显示边缘,前期对获取的未转换的数据进行了裁剪处理。裁剪处理过的点云数据不会影响转换的精度。
由图1可以看出,浅灰色点正确地处在深灰色点的缺口处,两站数据正确地拼接在一起,形成了完整的路面。说明转换后的点具有正确的坐标值。

图1 转换完的两站数据
图2是局部放大效果。由图中的粗线条可以看出,两站数据拼接的效果很好,说明本文算法转换的坐标精度是较高的。

图2 拼接处的放大效果
随着三维激光扫描技术应用范围的日益扩大,传统的逐站点配准点云数据的方法由于需要人工手动选点,效率低,且精度不能保证,故而难以适应多站点、大数据量的配准情况。而采用本文提出的坐标转换方法,既能实现点云的快速配准,又能保证精度,而且可以转换成1954北京坐标等应用范围比较广泛的坐标,也扩大了三维激光点云在实际中的应用。
六、结束语
七参数线性模型无法适用于旋角较大的情况。而本文提出的算法在大旋角的情况下仍然有很高的精度,受平移参数的影响也很小。算法实现快速,在扫描密度不高的情况下能实现实时转换。本算法较适合应用于将激光扫描仪数据进行三维坐标转换的情况。
[1] 杨伟,刘春,刘大杰.激光扫描数据三维坐标转换的精度分析[J].工程勘察,2004(3):61-63.
[2] 戴静兰,陈志杨,叶修梓.ICP算法在点云配准中的应用[J].中国图象图形学报,2007,12(3):517-521.
[3] 卢忠,归友龙,刘勇.基于总体最小二乘法的三维坐标转换参数解算[J].山西建筑,2009,35(36):359-360.
[4] 张宏.布尔莎-沃尔夫转换模型的几何证明[J].测绘与空间地理信息,2006,29(2):46-51.
[5] 柯金朴.空间三维坐标转换原理及实现[J].江西测绘,2008(3):16-20.
[6] 陈宇,白征东.基于非线性最小二乘算法的空间坐标转换[J].大地测量与地球动力学,2010(2):129-132.
[7] 陆珏,陈义,郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,28(5):77-81.
[8] BESL P J,MCKAY N D.A Method for Registration of 3D Shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.
Application of Unit Four Elements Method to Laser Point Cloud Coordinate Transformation
TENG Zhiyuan,ZHANG Aiwu
0494-0911(2010)11-0007-04
P237
B
2010-07-13
滕志远(1984—),男,山东威海人,硕士生,主要研究方向为三维信息获取与应用。
