2E12铝合金的高温塑性变形流变应力行为

黄裕金, 陈志国, 舒 军, 刘瑶琼, 周 娴

(中南大学 材料科学与工程学院，长沙 410083 )

2E12铝合金的高温塑性变形流变应力行为

黄裕金, 陈志国, 舒 军, 刘瑶琼, 周 娴

(中南大学 材料科学与工程学院，长沙 410083 )

通过在Gleeble−l500热模拟试验机上进行等温热压缩试验，研究2E12铝合金在变形温度为300~500 ℃和应变速率为0.0l ~ l0 s−1条件下的流变应力行为，计算、推导出用包含Arrhenius项的Zener-Hollomon参数描述2E12合金高温压缩流变行为的表达式，并分析形变热、变形温度和应变速率等参数对流变应力的影响规律。结果表明：应变速率和变形温度对2E12合金的流变应力影响显著，流变应力随着温度的升高而降低，随着应变速率的提高而增大；在ε˙≥1 s−1时，形变热导致流变应力降低，且幅度随着应变速率的增大而增大，随着变形温度的升高而降低。

2E12铝合金；热变形；流变应力；本构方程

2×24铝合金是耐疲劳损伤航空铝合金的典型代表，主要应用于机身蒙皮、机身框架和翼肋等重要结构材料。为了进一步满足更高的飞机安全性能和使用寿命的要求，美国铝业在2024铝合金的基础上，通过进一步降低Fe、Si杂质元素含量以及适当地限定主合金元素的成分范围，开发出了疲劳性能更优越的2524合金，并在Boeing777和Airbus380 等新型客机上得到广泛的应用[1−4]。与传统的2024-T3相比，2524-T3合金具有良好的室温力学性能及更优越的断裂韧性、抗应力腐蚀性能和抗疲劳性能，是目前飞机蒙皮的首选材料；2E12合金是我国在2524铝合金基础上研制的新型高性能铝合金。目前，有关2E12铝合金的研究主要是探讨其疲劳断裂机理[5−7]、 服役条件对其耐损伤性能的影响[5,8−9]以及热处理制度和合金化[10−13]等方面。

航空航天领域新设计理念[14]的提出，即以整体大构件代替组装小构件，对材料的热成型性能提出了更为苛刻的要求，而金属的热成型性能主要取决于金属热变形流变应力，因此，通过研究2E12铝合金高温塑性变形流变应力行为建立合理的流动应力模型，可以较准确地描述变形温度、变形程度以及变形速率等工艺参数对其流变应力的影响规律，为航空整体大构件热成型工艺的制定提供可靠的理论依据。鉴于此，本文作者在Gleeble−1500 热模拟试验机上对2E12铝合金圆柱试样进行等温压缩实验研究，探讨热变形时的流变应力与变形温度、应变速率的关系，采用一元线性回归法建立模型，并重点分析形变热、变形温度、应变速率等因素对流变应力的影响规律，为优化该合金整体大构件的热加工工艺提供理论依据。

1 实验

试验样品取自东北轻合金有限责任公司提供的半连续铸造扁锭，铸锭经过490 ℃、24 h均匀化退火，加工成尺寸为d10 mm×15 mm，两端带有d9 mm×0.2 mm 凹槽的Rastegaev 的样品，其轴向与铸造厚度方向平行。合金的化学成分(质量分数，%)为0.05Si、0.09Fe、4.45Cu、0.54Mn、1.50Mg，余量为Al。将加工好的试样在Gleeble−1500 材料热模拟试验机上进行等温压缩实验。压缩温度为300~500 ℃，应变速率为0.01~10 s−1，总压缩量为0.51(变形程度为40%)，样品采用热模拟机电阻加热，升温速度为2 ℃/s，压缩前保温3 min，试样两端的凹槽内填充75%石墨+20%机油+5%硝酸三甲苯脂，以减少摩擦对应力的影响。压缩过程中由Gleeble−1500热模拟机的计算机系统自动采集应力、应变、温度等数据，绘制出真应力—真应变曲线。

2 实验结果

2.1 真应力—真应变曲线

图1所示为2E12铝合金热压缩变形时的真应力—真应变关系曲线。由图1可见，在温度为300~500 ℃、应变速率为0.01~10 s−1的变形条件下，合金有明显的稳态流变特征，即在一定的应变速率和变形温度下，当真应变超过一定值后，真应变的增加对真应力变化的影响不大。

图1 2E12铝合金热压缩变形的真应力—真应变曲线Fig.1 True stress—strain curves of 2E12 alloys at different temperatures and strain rates

2E12合金在同一应变速率下，流变应力先随应变的增加迅速升高，但随着应变量的增加，应力—应变曲线的斜率逐渐减小，而且稳态流变应力随着变形温度的升高而降低；在同一变形温度下，流变应力随着应变速率的增大而增大，说明在该实验条件下该合金具有正的应变速率敏感性[15]，即应变速率越大，温度越低，合金达到稳态变形越困难。当应变速率为10 s−1时，合金在400 ℃以上温度变形时的应力—应变曲线上出现单波浪峰，并且随着变形温度的升高，该波浪峰表现得越明显，且当应变速率为0.01 s−1，温度为500 ℃时，应力—应变曲线上出现连续波浪峰。这些现象都与材料发生的动态软化过程有关。

2.2 2E12合金本构方程的建立

Zener和Hollomon的有关研究[15−18]表明，材料在高温塑性变形时，应变速率受热激活过程的控制，应力与应变速率之间的关系可用一项Z参数，即Zener-Hollomon参数表示：

式中：∆H为激活焓；R为摩尔气体常数；T为热力学温度；

研究[16]表明，在低应力水平的条件下，稳态流变应力(σ) 和应变速率(ε˙)之间的关系接近指数关系：

在高应力水平下，稳态流变应力和应变速率之间的关系接近幂指数关系：

SELLARS和TEGART[18]提出材料高温塑性变形在所有应力水平下的流变应力、应变速率和温度之间的关系可用包含变形激活能 (Q) 和温度 (T) 的双曲正弦形式修正的Arrhenius关系：

式中：A1，A2，A，α，n1,β和n分别为与温度无关的常数，且满足α=β/n1的关系；Q为变形激活能，通常与激活焓∆H相等，结合式(1)和(4)，可得：

分别对式(2)和(3)取对数，可知当温度一定时，n1和β分别为ln—lnσ和ln—σ曲线的斜率，采用一元线性回归处理，可得到ln—lnσ和ln—σ的关系曲线，且这2种线形关系的相关系数均大于0.99，如图2所示。将图2中曲线一元线性回归得到不同温度下的斜率n1和β，可算出不同温度下参数α。

图2 应变速率与流变应力的关系Fig.2 Relationship between strain rate and flow stress: (a) lnε˙—lnσ; (b) lnε˙—σ

对式(4)两边取自然对数的偏微分可得到：

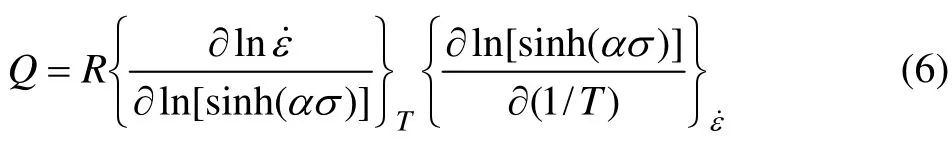
图3 流变应力与应变速率、变形温度的关系Fig.3 Relationships among deformation temperature, flow stress (a) and strain rate (b)

对式(5)两边取自然对数可以得到：

将所求的变形激活能、不同变形条件下的Z值、相对应的稳态流变应力σ和α一起代入式(7)，绘出lnZ与ln[sinh(ασ)]之间的关系曲线，如图4所示。可知温度补偿应变速率Z的自然对数和流变应力σ的双曲正弦项的自然对数间满足线性关系，说明可用包含Arrhenius项的Z参数来描述2E12合金在高温压缩变形时的流变应力行为，对图中数据进行一元线性回归分析，可求得A=2.151×1011s−1。综上所述，2E12合金材料常数的求解结果：变形激活能Q=154.8 kJ/mol，应力指数n=6.006，应力水平参数α=9.879×10−3MPa−1，结构因子A=2.151×1011s−1。将Q，α，n，A等材料参数值代入式(4)，得到2E12合金热压缩时的Arrhenius方程如下：

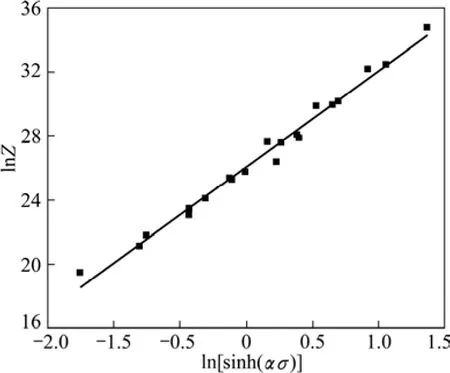
图4 流变应力与Z参数的关系Fig.4 Relationship between Zener-Hollomon parameter and flow stress

3 分析与讨论

3.1 温度对流变应力的影响

从真应力—真应变曲线中可以看出，温度的变化会对流变应力产生很大的影响。然而，金属在塑性变形时所消耗的大量能量，绝大部分转化为热能，小部分以储能的形式保留在金属中[20]。特别是当应变速率较大时，变形过程中产生的热量来不及散失，使试样的温度持续升高，很难保持恒温；在低应变速率条件下，大部分变形热通过夹具散失到环境中，产生的热量可以忽略。

DEVADAS等[21]的研究结果表明，温度变化对合金流变应力的影响可表示为

式中：Q=154.8 kJ/mol；R为摩尔气体常数；T为热力学温度；n、α为材料常数，分别取值为6.006、9.879×10−3MPa−1。

由变形热而引起的温度变化则可表示为

式中：ρ为合金密度；c为合金比热容；为实测的真应力—应变曲线下的面积，可表示为

以变形温度为400 ℃的情况为例，应变速率对试样温度的影响如图5所示。图5中应变速率低于1 s−1时的温度直接由计算机系统自动测定，而当应变速率为10 s−1时，由于变形时间短，受热电偶灵敏度的限制，采集的温度数据有限，且出现数据滞后现象，不能真实反映温升情况，此时温升通过理论计算得出。

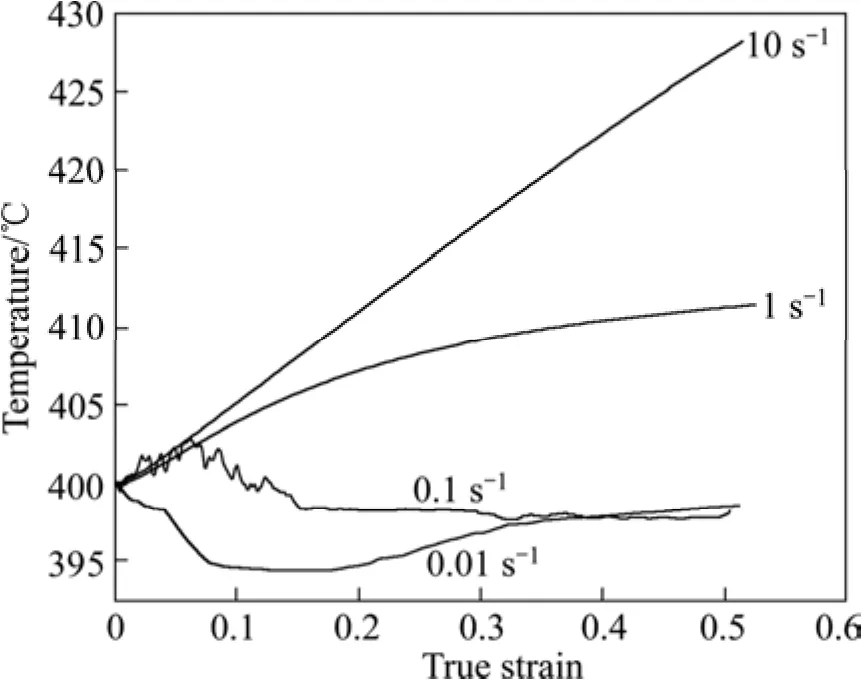
图5 预设温度为400 ℃时不同应变速率下热压缩过程中试样的测试温度Fig.5 Testing temperatures for specimens during compression tests at pre-set temperature of 400 ℃ and different strain rates

从图5 可以看出，在400 ℃变形时，随着应变速率的增大，温度升高越来越明显；当应变速率为10 s−1时，温度几乎随应变线性上升，当应变量达到0.5 时，温度达到428 ℃左右，比预设温度400 ℃高出28 ℃。而当应变速率在0.1 s−1以下时，温度的变化可由热模拟机的加热系统予以补偿，变形温度维持在400 ℃左右，基本为等温压缩。

图6所示为应变速率为10 s−1时，不同测试温度对试样最大温升的影响。从图6可以看出，测试温度越高，形变热对温度的影响越小，接近线性变化。这是由于测试温度越低，其流变应力越大，在相同的应变下所消耗的能量就越多，产生的热量越多，即温度升高越显著。

图6 测试温度与最大温升的关系Fig.6 Dependence of maximum increase of temperature on testing temperature during deformation

图7 预设温度为400 ℃时不同应变速率下2E12 铝合金修正前后的真应力—真应变曲线对比Fig.7 Comparison between corrected and uncorrected true stress—true strain curves for 2E12 aluminum alloys at preset temperature of 400 ℃ and different strain rates

表1 测试温度不同时修正前、后的流变应力最大差值Table 1 Maximum difference between uncorrected and corrected flow stress values at different testing temperatures

3.2 应变速率对流变应力的影响

从图1可以看出，在相同的变形温度下，流变应力随着应变速率的增大不断增大。这实质上与变形体内的位错密度紧密相关，许多学者认为这是变形引起的位错密度增加速率和动态回复导致的位错密度降低速率两者共同作用的结果，可用下式表示[22−24]：

式中：U为不可动位错的形成速率，与应变速率的关系较弱[21]；Ω为不可动位错的回复概率；ρ为位错密度。

对式(12)积分可得：

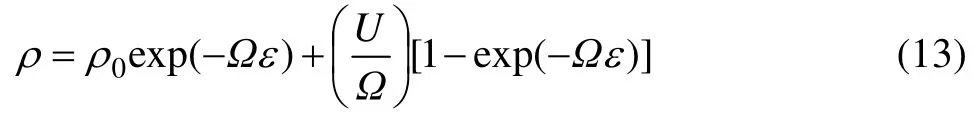
式中：ρ0为初始位错密度。当时，(其中ρs为加工硬化过程外延的饱和位错密度，对应的饱和应力为同时，引入经典应力—位错关系，可以得到下式[21]：

或

式中：σ0为初始应力，

由式(14)和(15)可知，流变应力随着Ω的增大而降低；随着U的增大而增大。在相同的测试温度条件下，基体内位错的增殖速率随着应变速率的增大而增大，而不可动位错回复概率不仅与应变速率有关，且与变形温度也有密切的关系。

利用式(15)对修正后的真应力—真应变曲线进行非线性拟合，即可得到一组有关Ω的经验值，如图8所示。从图8可以看出，Ω随着应变速率的增加而降低，且幅度随着变形温度的升高而增大，即在相同的测试温度条件下，不可动位错回复概率随着应变速率的增大而降低。

图8Ω与测试温度和应变速率的关系Fig.8 Dependence ofΩon testing temperature and strain rate

4 结论

1) 2E12铝合金经历过渡变形与稳态变形阶段，表现出稳态流变特征，应变速率和变形温度对合金的流变应力有显著影响，且合金的稳态流变应力随着变形温度的升高而降低；随着应变速率的增加而升高。

2) 在热变形条件下2E12铝合金的流变应力σ、应变速率ε˙与变形温度T满足关系式：

3) 在热变形过程中，尤其是快速、大应变条件下，由于形变热效应而使变形温度升高，导致流变应力下降，且这种效应随着测试温度的降低而增大。

REFERENCES

[1]WOJCIECHOWSKI S. New trends in the development of mechanical engineering materials[J]. Journal of Materials Processing Technology, 2000, 106: 230−235.

[2]SRIVATSAN T S, KOLAR D, MAGNUSEN P. The cyclic fatigue and final fracture behavior of aluminum alloy 2524[J]. Materials and Design, 2002, 23: 129−139.

[3]陈 文. 先进铝合金在A380上的应用[J]. 航空维修与工程, 2005(2): 41−42. CHEN Wen. Application of advanced aluminum alloys in A380 structures[J]. Aviation Maintenance and Engineering, 2005(2): 41−42.

[4]WARNER T. Recently-developed aluminum solutions for aerospace applications[J]. Materials Science Forum, 2006, 519/521: 1271−1278.

[5]SRIVATSAN T S, KOLAR D, MAGNUSEN P. Influence of temperature on cyclic stress response, strain resistance, and fracture behavior of aluminum alloy 2524[J]. Materials Science and Engineering A, 2001, 314: 118−130.

[6]DEBARTOLO E A, HILLBERRY B M. A model of initial flaw sizes in aluminum alloys[J]. International Journal of Fatigue, 2001, 23: 79−86.

[7]GOLDEN P J, JR GRANDT A F, BRAY G H. A comparison of fatigue crack formation at holes in 2024-T3 and 2524-T3 aluminum alloy specimens[J]. International Journal of Fatigue, 1999, 21: 211−219.

[8]杨 胜, 易丹青, 姚素娟, 钟 利. 温度对2E12铝合金疲劳性能与断裂机制的影响[J]. 航空材料学报, 2007, 27(6): 9−13. YANG Sheng, YI Dan-qing, YAO Su-juan, ZHONG Li. Effect of temperature on cyclic fatigue and final fracture mechanism of2E12 aluminum alloy[J]. Journal of Aeronautical Materials, 2007, 27(6): 9−13.

[9]杨 胜, 易丹青, 姚素娟, 钟 利. 腐蚀环境下2E12 航空铝合金疲劳裂纹扩展行为研究[J]. 材料工程, 2007(12): 26−34. YANG Sheng, YI Dan-qing, YAO Su-juan, ZHONG Li. Effect of corrosive environment on fatigue crack propagation of 2E12 aerospace aluminum alloy[J]. Journal of Materials Engineering, 2007(12): 26−34.

[10]杨 胜, 易丹青, 姚素娟, 钟 利. 热处理对2E12铝合金耐腐蚀性及力学性能的影响[J]. 金属热处理, 2007, 32(9): 9−13. YANG Sheng, YI Dan-qing, YAO Su-juan, ZHONG Li. Effect of heat treatment on corrosion resistance and mechanical properties of 2E12 aluminum alloy[J]. Heat Treatment of Metals, 2007, 32(9): 9−13.

[11]孙晓旭, 郑子樵, 陈圆圆, 李世晨, 魏修宇. 含Zr Al-Cu-Mg合金的微观组织与疲劳行为[J]. 中国有色金属学报, 2009, 19(1): 50−55. SUN Xiao-xu, ZHENG Zi-qiao, CHEN Yuan-yuan, LI Shi-chen, WEI Xiu-yu. Microstructures and fatigue behavior of Al-Cu-Mg alloy containing Zr[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(1): 50−55.

[12]李 海, 郑子樵, 魏修宇, 王芝秀. 时效析出对2E12铝合金疲劳断裂行为的影响[J]. 中国有色金属学报, 2008, 18(4): 589−594. LI Hai, ZHENG Zi-qiao, WEI Xiu-yu, WANG Zhi-xiu. Effect of ageing precipitation characteristics on fatigue fracture behavior of 2E12 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(4): 589−594.

[13]李 海, 王芝秀, 魏修宇, 郑子樵. 固溶处理时间对2E12铝合金组织和疲劳性能的影响[J]. 航空学报, 2009, 30(1): 148−152. LI Hai, WANG Zhi-xiu, WEI Xiu-yu, ZHENG Zi-qiao. Effect of solution treatment time on microstructures and fatigue properties of aluminum alloy 2E12[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(1): 148−152.

[14]HEINZ A, HASLER A, KEIDEL C, MOLDENHAUER S, BENEDICTUS R, MILLER W S. Recent development in aluminum alloys for aerospace applications[J]. Materials Science and Engineering A, 2000, 280: 102−107.

[15]蔡一鸣, 李慧中, 梁霄鹏, 汤国建. 7039 铝合金高温的热变形行为[J]. 中国有色金属学报, 2008, 18(10): 1775−1780. CAI Yi-ming, LI Hui-zhong, LIANG Xiao-peng, TANG Guo-jian. Thermal deformation behavior for 7039 aluminum alloy at elevated temperature[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(10): 1775−1780.

[16]WANG Y, LIN D L, LAW C C. A correlation between tensile flow stress and Zenner-Hollomon factor in TiAl alloys at high temperatures[J]. Journal of Materials Science Letters, 2000, 19(13): 1185−1188.

[17]吴文祥, 孙德勤, 曹春艳, 王战锋, 张 辉. 5083 铝合金热压缩变形流变应力行为[J]. 中国有色金属学报, 2007, 17(10): 1667−1671. WU Wen-xiang, SUN De-qing, CAO Chun-yan, WANG Zhan-feng, ZHANG Hui. Flow stress behavior of 5083 aluminium alloy under hot compression deformation[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(10): 1667−1671.

[18]SELLARS C M, TEGART W J. Hot workability[J]. International Metallurgical Reviews, 1972, 17(1): 1−24.

[19]李俊鹏, 沈 健, 许小静, 闫晓东, 毛柏平. 7050高强铝合金高温塑性变形的流变应力研究[J]. 稀有金属, 2009, 33(3): 318−322. LI Jun-peng, SHEN Jian, XU Xiao-jing, YAN Xiao-dong, MAO Bai-ping. Flow stress of 7050 high strength aluminum alloy during high temperature plastic deformation[J]. Chinese Journal of Rare Metals, 2009, 33(3): 318−322.

[20]MURTY S V S N, RAO B N, KASHYAP B P. Instability criteria for hot deformation of materials[J]. International Materials Reviews, 2000, 45(1): 15−26.

[21]DEVADAS C, BARAGAR D, RUDDLE G, SAMARASEKERA I V, HAWBOLT E B. The thermal and metallurgical state of steel strip during hot rolling: Part Ⅱ, factors influencing rolling loads[J]. Metallurgical Transactions A, 1991, 22: 321−333.

[22]BERGSTROM Y. A dislocation model for the stress—strain behavior of polycrystallineα-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations[J]. Material Science and Engineering, 1970, 5: 193−200.

[23]LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperatures and strain rates[J]. Metallurgical Transactions A, 1991, 22: 1545−1558.

[24]王 进, 陈 军, 张 斌, 赵 震, 阮雪榆. 35CrMo结构钢热塑性变形流动应力模型[J]. 上海交通大学学报, 2005, 39(1): 1784−1786. WANG Jin, CHEN Jun, ZHANG Bin, ZHAO Zhen, RUAN Xue-yu. The flow stress model of 35CrMo structural steel during hot forming[J]. Journal of Shanghai Jiao Tong University, 2005, 39(1): 1784−1786.

(编辑 杨 华)

Flow stress behavior of 2E12 aluminum alloy during hot plastic deformation at high temperature

HUANG Yu-jin, CHEN Zhi-guo, SHU Jun, LIU Yao-qiong, ZHOU Xian
(School of Materials Science and Engineering, Central South University, Changsha 410083, China)

The flow stress behavior of a hot compressed 2E12 aluminum alloy was investigated by compression tests performed on Gleeble−1500 tester at strain rates ranging from 0.01 s−1to 10 s−1and temperatures ranging from 300 ℃ to 500 ℃. The expression for describing the rheological behavior of 2E12 alloy during hot compression process by Zener-Hollomon parameter including Arrhenius term was deduced. The influence of temperature rise caused by deformation, testing temperature and strain rate on the flow stress was analyzed. The results show that the flow stress of 2E12 alloy is greatly affected by strain rate and temperature. The flow stress of 2E12 alloy decreases with increasing the temperature and rises with increasing the strain rate. At ε˙≥1 s−1, temperature rise caused by deformation results in reduced flow stress. The decrease of flow stress increases with increasing the strain rate and decreases with increasing the deformation temperature.

2E12 aluminum alloy; hot deformation; flow stress; constitutive equation

TG 146.2

A

国家重点基础研究发展计划资助项目(2005CB623705); 国家自然科学基金资助项目(50871123)

2009-12-14；

2010-04-12

陈志国, 教授, 博士; 电话: 0731-88830270; E-mail: hngary@163.com

1004-0609(2010)11-2094-07