基于刚柔结合建模技术的道岔区轮轨动力学仿真分析
2010-09-25罗雁云谭大正施董燕
罗雁云 谭大正 施董燕
(同济大学铁道与城市轨道交通研究院,201804,上海∥第一作者,教授、副院长)
道岔是轨道交通设备中的重要组成部分,同时也是轨道交通中最薄弱的环节之一。道岔区轨下不平顺会加剧列车过岔时的轮轨相互作用,降低列车运行的平顺性,从而导致道岔使用寿命的缩短。因此,为了提高列车过岔安全,改善列车运行的平顺性,有必要开展对道岔结构的动力学研究,而仿真分析是其中重要的技术手段之一。
过去在对车辆-轨道耦合系统进行动力学分析时,通常把车辆和轨道假设为刚性体,在此前提下建立的多刚体运动模型具有局限性,与实际情况有较大差异。事实上,钢轨本身的材料和结构具有弹性。在耦合系统中,钢轨一方面绕固定坐标系运动,另一方面相对自身局部坐标系做弹性变形运动,具有柔性体的特性。本文将主要研究对象道岔区的钢轨视作柔性体,次要对象车辆视为刚性体,利用耦合技术进行系统动力学仿真;目的是反映轨道结构柔性结构特征对整个车辆-道岔系统的影响,同时保留车辆为刚体,以减少求解难度、简化模型、提高仿真结果的精度。
1 车辆-道岔刚柔结合系统模型
1.1 刚柔体结合理论原理
运用有限元软件和多体动力学软件联合仿真创建刚柔结合系统模型。即在系统中将所关心的对象柔性化,以有限元方式创建一个仿真模型,然后将其模态分析结果与刚体模型集成。
通常采用两个坐标系描述多体系统中柔体的运动:一是惯性坐标系,另一是固定于柔性体上的局部坐标系。因此柔体中任意点P的运动为:

其中:r(t)和c是刚体运动矢量;u(c,t)是变形矢量,其Ritz近似为[1-2]:

其中:u(c,t)是模态振型uj(c)与模态坐标qj(t)加权的线性组合。模态振型 uj(c)可由有限元软件计算的固有特征振型与在静态载荷和约束作用下的静变形-静态振型内插得到,即:

为满足MBS(多体系统)方程的要求,需把柔体通过式(2)转化为弹性体运动方程:

式中:
b——加速度向量;
ω——旋转加速度;
q——变形加速度;
r——柔体上某单元相对局部坐标系原点的位置矢量;
M——惯性(质量)矩阵;
Kω(ω,q,q◦)— —阻尼向量阵;
K(q)——刚度向量阵;
h(r,q,…)——广义力向量阵。
其中加速度向量b由平动加速度a、旋转加速度 ω和变形加速度q三部分构成。因此产生的MBS方程所要求的柔体数据是必须计算的质量阵、阻尼阵和刚度阵。这些数据可预先进行计算,形成相应的标准输入数据文件以备使用。弹性体运动方程中的系数矩阵通过标准输入数据文件被传递给多体程序。也正是该文件提供的弹性体数据以及模态计算结果,才可以执行后续的整个运动方程的建立及进行多体系统仿真分析。
1.2 计算模型
本文以12号道岔为例,其辙叉区如图1所示。

图1 12号道岔可动心轨辙叉区结构示意图
在有限元软件和多体动力软件中,所创建的车辆-道岔耦合系统主要包括以下三部分:道岔区的轨道模型、车辆模型、轮轨接触模型。通过导入不平顺激扰模型,分析动荷载作用下轨道动力特性及轨下动刚度分布规律。
首先在PATRAN软件中创建道岔区的轨道模型,将其假定为均匀变截面梁(钢轨截面模拟为工字梁,如图2所示);计算模型的各阶固有频率,得到柔性体模态中性文件(*.mnf文件)。本文采用输出自由模态200阶,将结果导入ADAMS软件后发现同样受力方式下模型的变形与在PAT RAN软件中的变形能够很好地吻合,符合计算精度要求。

图2 变截面钢轨有限元模型
在ADAMS软件中建立车辆-道岔系统模型,车辆简化为带单个转向架的半车模型,包括车体、转向架、轮对、一系悬挂系统、二系悬挂系统。导入已生成的钢轨模态中性文件,生成道岔区轨道柔性体模型。
在刚柔结合模型中,如何处理刚性体和柔性体的接触问题是关键技术之一。在本文模型中,通过引入虚构件来解决。虚构件是一种质量和转动惯量都为零的刚体,没有任何质量信息,不会对模型的计算结果带来影响,但是可以解决ADAMS软件中柔性体和刚性体之间不能进行柔性连接的模型问题。本模型运用车轮与虚构件接触连接、虚构件与轨道单元固结的方式,简化了轮轨接触方式。接触形式使用碰撞函数Impact表示,非线性弹簧参数k=1×1012N/m,阻尼参数 cmax=1×104N。
1.3 道岔辙叉区轨下不平顺
研究在不平顺激扰下车辆通过道岔区时的轨道动力特性。不平顺在模型中是否恰当表达,对最后结果的输出分析有直接的影响。道岔区存在不平顺主要是指复杂的结构造成的几何不平顺以及轨下刚度不平顺。几何不平顺在道岔心轨区较为明显。根据《道岔设计手册》,将在竖直面上出现的几何不平顺在模型中采用纵向L=0.8 m、竖向h=3 mm的三角体来模拟,如图3所示。
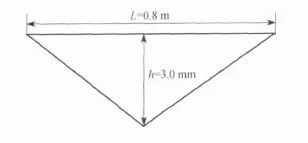
图3 几何不平顺简化模型
道岔辙叉区轨道刚度不平顺是指轨道竖向刚度大且沿纵向分布不均匀,在辙叉、心轨等部位的轨道刚度呈跳跃性变化。随着列车速度的提高,道岔辙叉区轨道刚度的严重不均匀加重了道床及道岔部件的损伤。根据轨道刚度分布规律[3],道岔中的连接轨主要有三个刚度突变点,最大值达256 kN/mm。本文采取弹性元件阻尼器的刚度输入法来模拟刚度不平顺,不仅能直观地输入轨道竖向刚度值,而且通过设置移动特性的横向和纵向刚度最大值、转动特性的三向刚度最大值,而使轨道在动力仿真过程中保持横向、纵向和转动的稳定性,为研究道岔竖向刚度不平顺对整个轮轨系统的动力特性提供了条件。
2 动力学仿真及结果
2.1 不同速度通过道岔辙叉区对系统动力特性的影响
图4和图5分别为车辆以200 km/h的速度直向通过道岔时,心轨尖端轮下钢轨竖向振动和竖向位移。图4、5中的两个峰值,分别是两对车轮前后通过心轨尖端所产生的轨道振动和位移。可见心轨尖端轮下钢轨最大振动加速度为948 m/s2,竖向位移为0.95 mm。由此可知,车辆通过道岔时,由于心轨尖端刚度大且存在几何不平顺,振动比较剧烈,在设计中,应保证此处的竖向稳定性,防止钢轨倾覆。
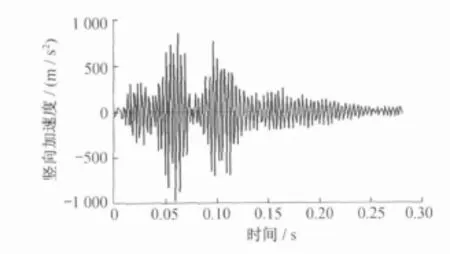
图4 道岔心轨尖端处轮下钢轨竖向振动加速度
表1所示为该模型在列车 120、160、200、250 km/h速度下直向过岔时,基本轨、连接轨和心轨尖端的竖向位移和竖向加速度的最大值。比较同一速度下基本轨和连接轨的最大加速度,基本轨的最大竖向位移大于连接轨的最大竖向位移,基本轨的最大竖向加速度小于连接轨的最大竖向加速度。当列车直向过岔速度为200 km/h时,连接轨加速度比基本轨竖向加速度高出4.5%。从图6和图7也可以看出,随着车辆过岔速度的增大,基本轨、心轨尖端的竖向加速度接近于连接轨最大竖向加速度。当过岔速度为250 km/h时,基本轨最大竖向加速度比200 km/h时增大约40%,连接轨最大竖向加速度约增大42%,心轨尖端最大竖向加速度增大约38%。连接轨和心轨尖端的最大竖向位移在250 km/h速度时,比200 km/h速度时增加 0.3%,基本轨的最大竖向位移随着速度而变化,但变化较小。
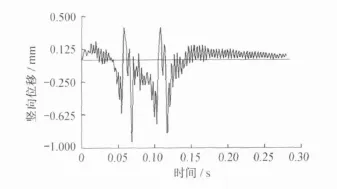
图5 道岔心轨尖端处轮下钢轨竖向位移
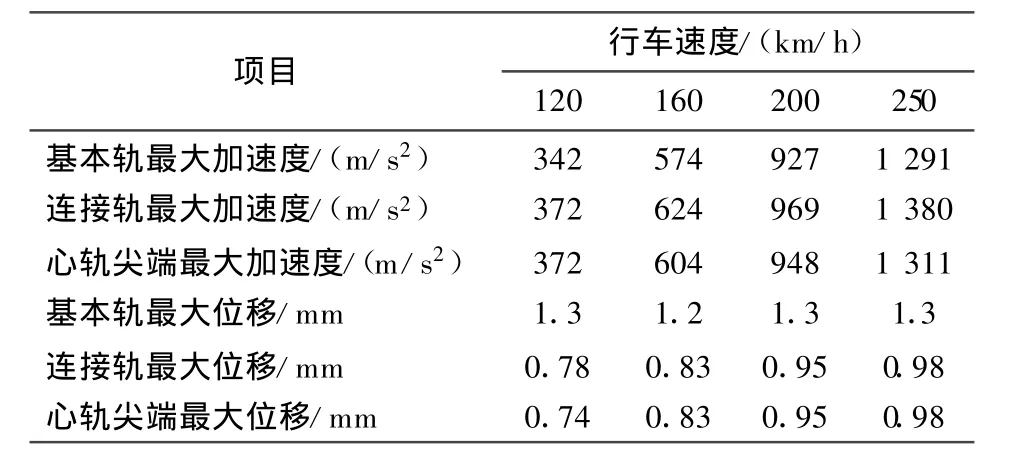
表1 不同速度下道岔不同部位轮下钢轨竖向加速度和竖向位移最大值
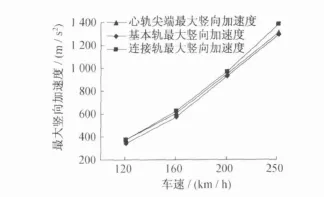
图6 轮下钢轨竖向加速度随车辆通过速度的变化

图7 轮下钢轨竖向位移随车辆通过速度的变化
2.2 几何不平顺对道岔辙叉区轮轨动力特性的影响
计算结果表明,车辆以200 km/h速度通过时,道岔辙叉区存在几何不平顺的情况下,车体在心轨尖端处产生竖向加速度和竖向位移的峰值;不考虑几何不平顺时,车体在同样位置不产生竖向加速度和竖向位移的峰值,而且此时轮下钢轨竖向位移要比有几何不平顺时的位移小50%,轮下钢轨竖向加速度要减小84%(如图8所示)。这说明几何不平顺是系统振动的激励源之一。
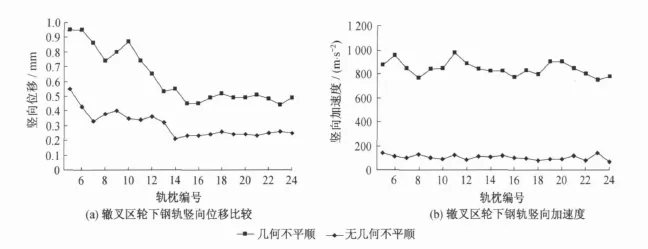
图8 车辆以200 km/h速度通过时道岔辙叉区轮下钢轨竖向位移和竖向加速度比较
2.3 刚度不平顺对道岔辙叉区轮轨动力特性的影响
文献[3]采用改变连接轨轨下胶垫刚度,按照一定规律将道岔轨下刚度分布进行了优化,以达到改善道岔轨下刚度的均匀分布。模型参考该优化方案,分析了刚度平顺性优化前后道岔辙叉区轨下刚度改变对轮轨动力特性的影响(详见表2)。从表2可以看出,轨下刚度平顺性优化前后,车辆的轮对、转向架和车体的竖向加速度有所减小(车体约减小7%,转向架约减小2%,轮对约减小1%)。这说明轨下刚度的合理设置,有助于减小车辆主要部件的振动,对车辆运行平顺性的提高有一定的帮助。而对道岔的基本轨、连接轨和心轨尖端的竖向加速度有所减小(减小幅度在3%~5%左右)。由于平顺性优化前后基本轨轨下刚度不变,基本轨除了磨耗产生的不平顺外,没有像心轨处那样明显的集中性不平顺,故其最大竖位移不变;而平顺性优化后的连接轨、心轨尖端处的轨下刚度减小,使最大位移略有增大。

表2 轨下刚度平顺性优化前后车辆-轨道动力特性比较
2.4 道岔辙叉区动刚度分布规律
轨道竖向动刚度是指作用在钢轨上某点的竖向激振力幅值与该点钢轨竖向动位移幅值之比。它反映了某一瞬态受迫振动下的轨道刚度特性。本文是基于刚柔结合建模的多体系统,仿真中考虑了钢轨的弹性特征,计算得出的动应变和动应力结果也为研究道岔辙叉区轨道动刚度分布规律提供了可能。
现按照动刚度的计算方法(即作用力幅值与动位移幅值之比),在考虑几何不平顺和刚度不平顺的4种组合工况下,比较道岔辙叉轨道动刚度与静刚度大小(如图9所示)。
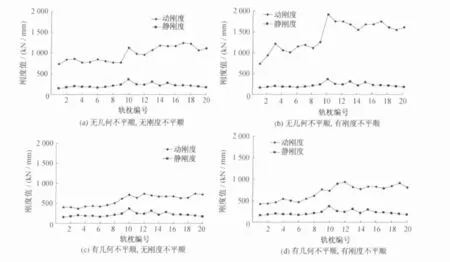
图9 道岔辙叉在不同工况下轨道动刚度与静刚度的比较
由图9可见,在不同工况下动刚度是变化的,其变化幅度也会不同。道岔辙叉区的轨下刚度不平顺严重,则轨道动刚度与静刚度之比就有较大的偏差,因此轨道动刚度参数反映了轨道不平顺对其有较大的影响。
3 结语
基于刚柔结合建模,建立了把道岔辙叉区轨道视为弹性体、车体视为刚性体的车辆-道岔耦合系统模型,分析在道岔辙叉区轨道几何不平顺及刚度不平顺状态下的轮轨系统动力特性。通过PATRAN与ADAMS软件的联合仿真,计算了道岔辙叉区在各种不平顺条件下车体和轨道的动应变及动应力。结果表明,道岔辙叉区几何不平顺是车体振动的激励源之一,轨下刚度分布是否均匀也直接关系到高速运行下列车的稳定性和旅客的舒适性。
通过对仿真结果的分析,发现将轨道视为弹性体比过去视为刚性体的计算结果偏小,但基本反映了在车辆通过道岔辙叉区时的轮轨振动规律;进而还分析了在4种工况下道岔辙叉区轨道动刚度的分布规律。可以看出,道岔辙叉区的静刚度不平顺分布对轨道瞬时动刚度也会产生较大的影响;道岔辙叉区轨道静刚度不平顺严重,则相应的轨道动刚度与静刚度之比也有较大的差异。因此,在道岔轨下刚度平顺化设计中,只考虑静刚度是不够的;动刚度分布规律为道岔辙叉区轨道刚度的优化提供了参考依据。
[1]Dietz S,Hippmann G,Schupp G.Interaction ofvehiclesand fiexible tracks by co-simulation of multibody vehicle sy stems and finite element track models[J].Vehicle Sy stem Dynamics Supplement,2003,37:372.
[2]Andersson C,Abrahamsson T.Simulation of interaction between a train in general motion and a track[J].Vehicle System Dynamics,2002,38(6):433.
[3]Wallrapp O.Flexible bodies in multibody sy stem codes[J].Vehicle System Dy namics,1998,30(3):237.
[4]金新灿,孙守光,陈光雄.车辆通过道岔时转向架结构系统振动特性研究[J].工程力学,2007,24(1):179.
[5]王平.道岔区轮轨系统动力学的研究[D].成都:西南交通大学博士学位论文,1997.
[6]谭晓春.道岔轨下刚度平顺性与动态特性关系研究[D].上海:同济大学硕士学位论文,2008.
[7]谭晓春,罗雁云.轨道交通列车过岔振动特征研究[J].城市轨道交通研究,2008(1):28.
[8]朱剑月,顾福民,罗雁云.道岔尖轨轨下刚度改变对轮轨动力性能的影响[J].同济大学学报,2002,30(2):198.
