型钢混凝土框架振动台试验的有限元模拟

熊爱国，季 静，2

（1.华南理工大学 土木与交通学院，广东 广州 510640；2.亚热带建筑科学国家重点实验室，广东 广州 510640）

型钢混凝土框架振动台试验的有限元模拟

熊爱国1，季 静1，2

（1.华南理工大学 土木与交通学院，广东 广州 510640；2.亚热带建筑科学国家重点实验室，广东 广州 510640）

基于纤维模型和动力相似理论，利用ETABS和PERFORM-3D分析软件对一缩尺比例为1/8的平面三层型钢混凝土框架结构进行了整体结构弹性、弹塑性分析和推覆分析。将所得动力响应值与振动台试验实测结果进行对比，验证了8度小震、中震、大震作用下结构的抗震能力，研究结果表明型钢混凝土结构具有较大的水平抗侧刚度及弹塑性分析软件PERFORM-3D适用于模拟振动台结构模型的抗震性能分析。

纤维单元；弹塑性时程分析；型钢混凝土框架；振动台试验

引言

现代工程界普遍采用的有限元数值模拟分析和设计建筑结构过程中，主要利用塑性铰模型和纤维模型来模拟结构和构件的非线性属性。一般通用的有限元软件 （如ETABS、SAP2000）采用的是塑性铰模型，塑性铰模型需要输入由构件材料属性和几何特性决定的力-位移等形式的关键数值点，但一个整体结构因为建筑功能和造价大小等因素的影响往往导致构件的截面和材性组成等形式变化多样，特别是对于复杂高层结构和特殊结构，造成了塑性铰模型运用的不方便。大多数工程需要的情况下，为了统一而选择有限元软件默认的塑性铰，对于实际结构构件模拟并没有达到真正的同一性。纤维模型从单轴材料本构关系出发，实现了结构构件之间的真正同一性，能精确模拟结构和构件的非线性响应，在工程分析和设计中已经应用并逐渐推广。

1 纤维模型理论

1.1 概念

所谓纤维单元模型又称截面离散单元[1]（Discretized-Section Model），就是将构件截面划分成沿着长度方向的若干纤维，每根纤维均为单轴受力，并用材料单轴应力-应变关系来描述该纤维材料的受力特性，只适用于几何线性小变形理论，纤维间的变形协调则采用平截面假定。

1.2 基本特点和假定

对于长细比较大的杆系结构，纤维模型具有以下特点[2]：（1）纤维模型将构件截面划分为若干混凝土纤维和钢筋纤维，用户可自定义每根纤维的截面位置、面积和材料的单轴本构关系，适用于各种截面形状；（2）纤维模型可以准确考虑轴力和 （单向和双向）弯矩的相互关系；（3）由于纤维模型将截面分割，因而同一截面的不同纤维可以有不同的单轴本构关系，这样就可以采用更加符合构件受力状态的单轴本构关系，如可模拟构件截面不同部分受到侧向约束作用 （如箍筋、钢管或外包碳纤维布）时的受力性能。

基于杆系结构力学和一维材料本构的纤维模型[3]，是分析混凝土框架结构非线性行为较好的数值模拟方法，应用范围较广，但纤维模型单元的应用也是建立在下列假定条件基础上的：（1）基于几何线性小变形假定；（2）满足平截面假定；（3）一个梁单元划分为若干个积分段，在每段内截面形式以及截面上各个纤维的本构关系保持一致；（4）忽略粘结滑移和剪切滑移影响；（5）认为扭转是弹性的且与弯矩，轴力不耦合。

2 缩尺振动台试验模型

2.1 动力相似理论

在对结构进行抗震性能研究的振动台试验中，需要模拟原型结构的惯性力、恢复力和重力三种力，为了更好反应结构原型的动力特性，模型的设计应该依据动力相似理论[4]。相似条件包括平衡、相容性、边界和初始条件，然而在实际振动台模型试验中并不能完全满足上述相似条件，但从研究结构的整体抗震性能来考虑的话，应侧重于模型与原型结构抗侧力构件的相似。

为了达到模型与原型结构相似的目的，模型设计必须满足下列公式 （1）动力相似平衡方程，由于模型缩尺比例已知，即SL：尺寸相似系数，则式中有三个主要相似控制参数。SE：弹性模量相似系数，Sa：加速度相似系数，Sρ：材料密度相似系数。根据材料法则的相似性要求，模型与原型应具有相同的应力应变关系，即模型与原型结构的竖向压应变相似常数Sε=1或SE=Sσ。故要求模型材料必须与原型一样，或两者具有如图1所示的应力-应变曲线关系[5]。

图1 相似材料应力-应变曲线Fig.1 Stress-strain relationship of similar material

2.2 试验模型

本文的研究背景是西安建筑科技大学赵鸿铁、薛建阳等人在单向电液伺服振动台上进行的型钢混凝土框架结构地震模拟振动台试验，试验数据是从论文［6］［7］上获取。试件为两跨三层的平面型钢砼框架，缩尺比例为1/8，抗震设防烈度为8度，场地类别为Ⅱ类，试件结构荷载和构造等要求按照相关结构设计和抗震设计规范[8]进行，具体参照上述文献。

2.2.1 试件材料和尺寸

试件平面和主要试件结构构件截面的几何尺寸如图2所示，钢骨由焊接钢板构成，纵向钢筋和箍筋分别由14#和18#镀锌钢丝替代，梁端和柱端箍筋加密。混凝土采用细石混凝土，试验前实测立方体抗压强度为33.6 MPa，相关材料材性试验结果和性能参数如表1所示。

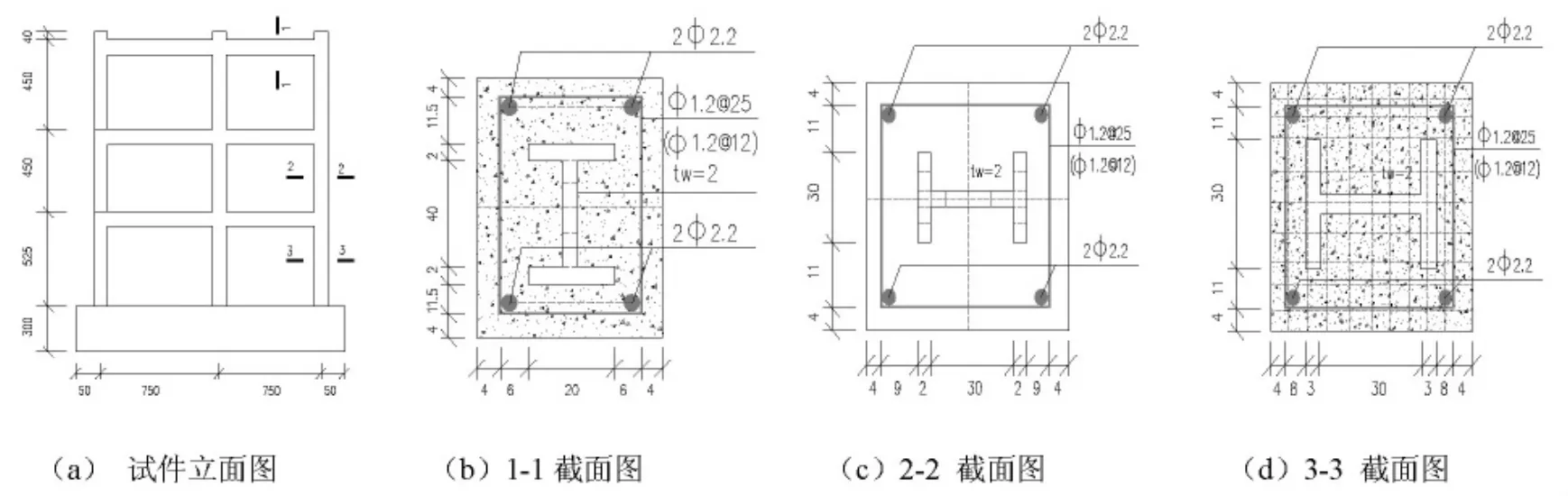
图2 试件立面和构件截面图Fig.2 Elevation drawing of test specimen and section drawing of components

表 1 材料材性参数Table 1 Parameters of material characteristics

2.2.2 相似系数

由于振动台的台面承载能力和试验可操作性，试件模型只能选择欠质量配重模型［9］，所加配重值为原设计相似配重的64%，为了满足模型试验的相似关系，地震动加速度时程波的时间轴相似比为1/3.6，根据量纲分析理论，结合参考论文和相关文献［10］［11］推导了模型与原型的主要相似关系，如表2所示。

2.2.3 试验过程

试验选择输入的地震动加速度时程为EL-Centro波，其主要强震部分持续时间大约26 s，记录全部波形长54 s，原始记录离散加速度时间间隔为0.02 s，选择输入的N-S分量加速度峰值为341.7 gal。在输入振动台地震波之前，为了获得试件模型的模态动力特性，进行了顶点敲击试验。根据时间相似比例关系和地震波的强震记录情况，对输入的时程波进行压缩[12]，时间间隔为0.006 s，输入地震记录长度为4.02 s。依据地震设防烈度和加速度相似比关系，按照逐级加载的方式，分别输入的加速度峰值为0.16 g、0.31 g（规范设计加速度峰值X加速度相似系数，中震）、0.53 g、0.61 g（规范设计加速度峰值X加速度相似系数，大震），实测了结构在弹性和弹塑性阶段的动力响应值。

3 数值模拟分析和试验结果

3.1 分析软件

PERFORM-3D软件与一般通用有限元软件ETABS相比，具有较好的三维结构弹塑性分析能力，专门用于工程抗震设计和研究，适用于对整体结构进行动力弹性、弹塑性分析和推覆分析。文章 ［13］［14］中选取纤维模型的塑性区单元，利用PERFORM-3D对带有型钢构件的复杂高层结构模型进行建模和分析，并指出纤维模型相对于塑性铰模型在模拟结构阻尼过程中的一个优点：基于多折线材料本构的纤维模型在构件变形的全过程中，随着纤维的开裂，屈服及破坏，附加阻尼自动计算。

PERFORM-3D可以根据实测结果输入钢材和混凝土等材料的应力-应变关系曲线，取用的钢材和混凝土本构曲线模型是无下降段的三折线应力-应变关系曲线，如图3所示。模型中型钢梁和柱的钢骨、钢筋及混凝土等材料都是独立地通过纤维截面，以水平和竖向坐标为定位及单个纤维面积整体输入，具体划分方式见上图2中的虚线，但由于简化计算时间和考虑到有足够计算精度的前提下，截面的纤维数目有一定限制。

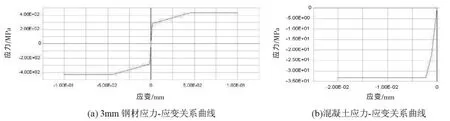
图3 PERFORM-3D材料应力-应变关系曲线Fig.3 Stress-strain relationship of materials in PERFORM-3D program

为了合理模拟型钢框架结构的地震响应，选取一维纤维单元模拟梁，二维纤维单元模拟柱，典型的非线性梁柱单元组成如图4所示。考虑到型钢框架的节点区连接构造和强节点的设计原则，且在试验过程中试件的节点设置了加强角钢，故在梁柱单元端部设置了自动刚性区域。参照型钢构件塑性区长度Lp[15]计算公式 （2），利用弹塑性截面分析软件XTRACT计算型钢梁柱构件的截面屈服弯矩和极限弯矩等推导出构件的塑性区长度Lp，其中以底柱截面为例计算结果如图5所示。

图 4非线性构件示意图Fig.4 Schematic map of nonlinear components

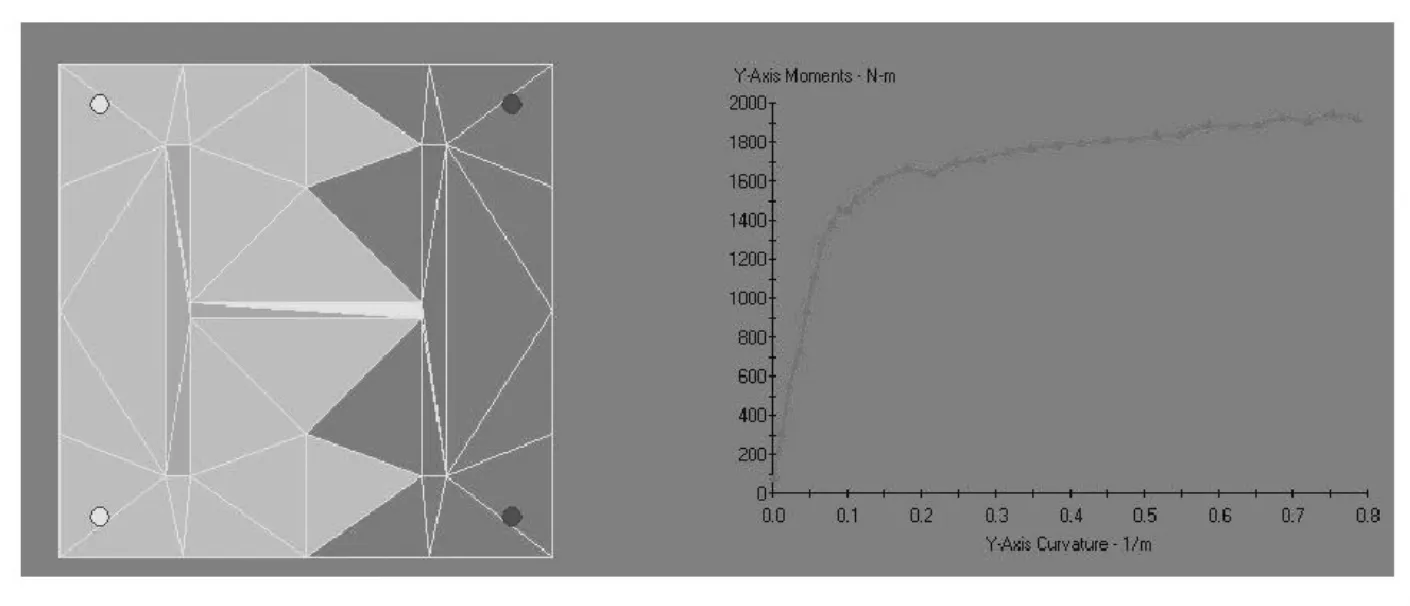
图5 截面弯矩-曲率曲线Fig 5 Moment-curvature curve of section

其中Mmax，My分别是截面的极限弯矩，屈服弯矩；Z是极限状态下杆端截面到反弯点的距离。

3.2 模态分析

首先用软件PERFORM-3D和ETABS分别建模并进行模态分析，所得的结果与试件模型的实测模态动力特性进行比较，由于在振动台敲击试验当中的高频信号较弱，只能获取到前两阶模态特性值，如表3所示。由表可知，主要结果比较吻合，结构模型合理可靠。

表 3 模态分析结果比较Table 3 Comparison of modal frequency analysis

3.3 弹性分析

由PERFORM-3D软件分析时程荷载作用下的能量图，如图6所示，整个试件模型随着时程荷载的逐级输入，可以清楚看到模型整体结构从弹性向弹塑性发展的过程。另外为了进一步验证模型的合理性，同时也为了解结构模型在弹性阶段小震作用下的动力响应特性，利用软件ETABS和PERFORM-3D分别对所建模型补充进行了整体结构小震作用下的弹性时程分析，输入时程波的加速度峰值为0.12 g（小震），顶部位移反应时程对比如图7所示，其中在ETABS中钢骨截面是通过section-builder设置的。

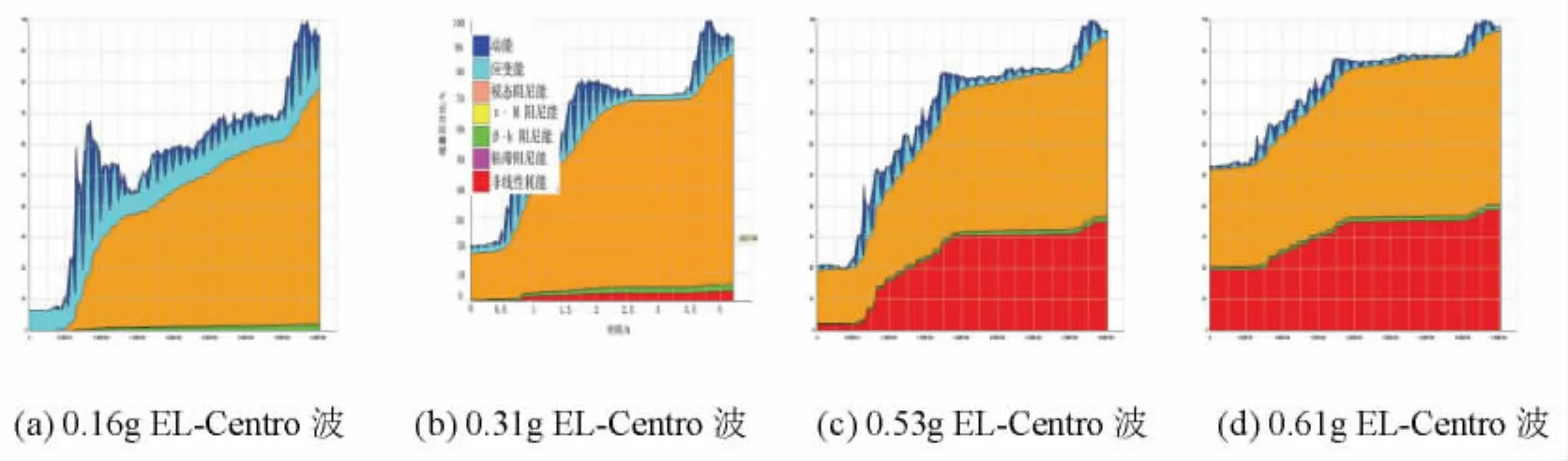
图6 PERFORM-3D模型结构能量耗散时程图Fig.6 Energy dissipation response form time-history analysis in PERFORM-3D program

图7 PERFORM-3D与ETABS弹性时程分析对比Fig.7 Comparison of elastic time-history analysis results from PERFORM-3D program and ETABS program

由上述整体结构模型分析的能量耗散时程图可推知，小震作用下 （0.12 g）结构完全处于弹性状态。小震作用下结构顶点最大位移值为1.02 mm，即所求层间位移角1/1 425远小于抗震设计规范对普通框架结构弹性层间位移角1/550的限值，说明型钢混凝土框架结构具有很好的水平抗侧刚度和变形能力。

3.4 弹塑性分析

该型钢混凝土框架试件模型利用PERFORM-3D软件进行动力弹塑性分析，数值模型采用瑞利阻尼，可以考虑阻尼比在结构高阶模态的变大，目前系数α、β如何取值并不明确，但通过常数阻尼比和模态周期可以计算出来，即输入结构实测第一振型阻尼比0.03，并设置Tb=0.9T1，Ta=0.2T1。由能量耗散时程图可知，整体结构模型从输入加速度峰值0.31 g的EL-Centro压缩波开始进入弹塑性阶段，即中震作用下开始出现了塑性变形 （能量图中红色），且随着加速度峰值的逐级输入，塑性变形耗散能量所占百分比越来越大。为了能得到与试验值相吻合的理论分析结果，在数值模拟分析过程中考虑到了构件的P-Δ效应，将整个加载过程中的楼层顶点最大加速度理论值与实测值进行了比较，如表4所示。

表4 PERFORM-3D分析与实测顶层加速度最大值对比Table 4 Comparison of the top layer's maximum acceleration of PERFORM-3D program and shaking table test

由上表可知，PERFORM-3D模型分析值与实测顶点最大加速度值较接近，整体结构模型在弹性向弹塑性发展的过程中，顶层的加速度最大值是逐渐增大，但动力放大系数是逐渐减小，这是材料的非线性和构件破坏的发展，整体结构刚度退化和阻尼比增大的结果，说明了所建模型可靠合理。分析误差在弹性阶段较大，而在弹塑性阶段与实测值相近，原因是软件分析的开始阶段没有模拟试验开始阶段为了得到结构模态特性的敲击模态试验过程及造成整体结构的累积损伤误差，当整体结构进入弹塑性阶段以后损伤误差值相对较小，可以忽略不计。

中震 （0.31 g）和0.53 g EL-Centro时程波作用下，将PERFORM-3D模型计算分析的楼层整体位移和楼层剪力分别与试验结果进行对比，如图8所示，且楼层剪力试验值是根据实测各层最大加速度反应乘以相应层的质量叠加后得到的。同时将PERFORM-3D模型在0.53 g EL-Centro时程波作用下计算分析的楼层顶点最大位移时程曲线与实测位移时程曲线对比，如图9所示。

图8 PERFORM-3D弹塑性时程分析与试验值对比Fig.8 Comparison of elastic time-history analysis results from PERFORM-3D program and shaking table test

图9 PERFORM-3D弹塑性位移时程分析与试验值对比Table.4 Comparison of elastic-plastic time-history analysis displacements of PERFORM-3D program and in shaking table test

从对比结果可知，图形变化趋势一致，数值模拟与试验值基本吻合，楼层整体位移和顶点时程位移的分析值与实测值之间误差都小于8%，楼层剪力的平均误差也都小于15%，综合考虑整个试验的过程和数值模拟分析的方法，出现误差的主要原因如下：（1）试验和数值模拟分析过程中，实际都存在并考虑了结构的重力二阶效应，但在计算模型与原型相似系数时取用的是忽略重力影响的计算公式；（2）在对输入时程波进行压缩和数值点取样的过程中有差异，导致分析或试验过程中出现个别奇异峰值点，产生了共振现象；（3）由于数值模拟分析过程中模型构件是软件默认的连接方式，而在试验过程中采取了对试件构件连接部位加强的措施。但总的来说，中震作用下的数值模拟分析结果是可以接受的。

大震 （0.61 g EL-Centro波）作用下，由于试验过程中实测数据缺省，故为了验证大震作用下PERFORM-3D时程分析结果的有效性，基于该弹塑性分析模型，在倒三角形荷载作用下进行了推覆分析作为弹塑性时程分析的参考，结构模型正X方向推覆变形和能力谱验算结果分别如图10、11所示。能力曲线与需求谱曲线的交点 （性能点）坐标：20 869N，20.8 mm；需求层间位移角：1/69；与需求点相对应的加载步/总加载步：14/20。大震作用下结构整体弹塑性时程分析与推覆分析性能点时刻的层间位移角对比，如图12所示。

图10 正X方向推覆变形图Fig.10 The overthrust deformation in normal X direction

图11 正X方向推覆能力谱验算图Fig.11 The curve of overthrust ablility in positive X direction

图12 结构层间位移角曲线图Fig.12 The angle of displacement curve of structural model

分析结果表明大震作用下的结构变形性能满足需求谱需求，层间位移角小于混凝土框架结构弹塑性限值1/50，结构达到了大震作用下抗倒塌的性能目标，结构在推覆分析和弹塑性时程分析下的层间位移角的整体变化趋势一致且对应数值相近，即大震作用下的结构整体弹塑性时程分析结果是可信的。

4 结论

通过基于纤维模型的抗震设计与分析研究软件PERFORM-3D对缩尺型钢混凝土框架结构振动台试验的动力响应进行数值模拟，采用相似强度模型，对结构的整体弹性和弹塑性能进行了分析研究。为了更好理解目标模拟分析型钢混凝土框架结构的抗震性能，结合现行设计规范对模型结构在8度小震、中震及大震时程荷载作用下的整体动力响应与试验实测值比较分析研究，可以得到以下结论：

（1）PERFORM-3D软件适用于对型钢混凝土框架振动台试件数值模拟，在几何尺寸、材料属性、边界条件、荷载大小和质量分布等方面都能满足试验要求，另外软件的整体分析步骤简单且结果输出容易，具有实际工程应用意义。

（2）基于纤维模型单元和相似理论的弹塑性分析方法可以准确模拟缩尺模型结构构件的弹塑性行为，能快速完成对整体结构的抗震性能分析，能量耗散时程图可以反映出整体结构从弹性向弹塑性阶段发展的全过程。

（3）小震作用下的弹性时程分析和部分模态动力特性的比较结果表明，所建模型合理可靠，结构层间位移角远小于结构规范对混凝土框架结构的限值，故型钢混凝土框架具有很好的水平抗侧刚度和变形能力。中震和大震作用下的弹塑性时程分析，从所得结果与试验实测值及推覆分析值的对比，可以看出模型结构的整体弹塑性分析结果是可信的。

［1］吕西林,卢文生.纤维墙元模型在剪力墙结构非线性分析中的应用 ［J］.力学季刊,2005,26(1)：72-80.

［2］韩小雷,陈学伟,林生逸.基于宏观单元的结构非线性分析方法、算例及工程应用 ［J］.工程力学,27 (S1)：59-67.

［3］韩小雷,陈学伟,郑宜,等.足尺钢框架振动台试验及动力弹塑性数值模拟 ［J］.地震工程与工程振动, 2008,28(6)：134-141.

［4］杨旭东.振动台模型试验若干问题的研究 ［D］.北京:中国建筑科学研究院,2005.

［5］Xilin Lu,Ying Zhou,Wensheng Lu.Shaking Table Model Test and Numerical Analysis of a Complex Highrise Building［J］.The Structural Design of Tall and Special Buildings,2007,16：131-164.

［6］薛建阳,赵鸿铁.型钢钢筋混凝土框架振动台试验及弹塑性动力分析 ［J］.土木工程学报,2000,33(2)：30-34.

［7］薛建阳,赵鸿铁.型钢混凝土框架弹塑性地震反应试验研究 ［J］.西安建筑科技大学学报：自然科学版, 1997,29(4)：361-363.

［8］GB50011-2001,建筑抗震设计规范 ［S］.北京:中国建筑工业出版社,2001.

［9］孟庆利.地震模拟模型实验中RC结构非线性性态模拟研究 ［J］.地震工程与工程振动,2008,28(6)：97-105.

［10］吕西林,李培振,陈跃庆.12层钢筋混凝土标准框架振动台试验的完整数据 ［R］.上海：同济大学土木工程防灾国家重点实验室,2004.

［11］黄维平,邬瑞锋,张前国.配重不足时的动力试验模型与原型相似关系问题的探讨 ［J］.地震工程与工程振动,1994,14(4)：64-71.

［12］宗周红,林东欣,房贞故.两层钢管混凝土组合框架结构抗震性能试验研究 ［J］.建筑结构学报,2002, 23(2)：27-35.

［13］韩小雷,唐建秋,黄艺燕,等.钢管混凝土巨型斜交网格筒体结构非线性分析 ［J］.地震工程与工程振动, 2009,29(4)：77-84.

［14］韩小雷,陈学伟,林生逸等.基于纤维模型的超高层钢筋混凝土结构弹塑性时程分析 ［J］.建筑结构，2010，40（2）：13-16.

［15］白国良,楚留声,朱丽华.型钢混凝土框架静力非线性分析塑性铰参数研究 ［J］.西安建筑科技大学学报：自然科学版,2007,39(6)：756-761.

Abstract：Based on fiber element model and the law of dynamic similarity,the SRC-frame model,a three-story plane model with the scale factor of 1/8,was created by ETABS and PERFORM-3D software.Analysis of the whole structure model,which included elastic time history analysis,elastic-plastic time history analysis and push-over analysis,was applied by the ETABS and PERFORM-3D software.This paper compared dynamic response of different earthquake actions between the numerical simulatation analysis results and the experimental results of shaking table test.The comparison confirmed the seismic capacity of the structure model under frequent,moderate and rare earthquake in this paper.So the study indicated that the SRC-frame had a large horizontal level stiffness and PERFORM-3D software was suitable to simulate the seismic performance analysis of model of shaking table test.

Keywords：Fiber element;Elastic-plastic time history analysis;SRC-frame;Shaking table test

Finite Element Simulation of Steel Reinforced Concrete Frame Model of Shaking Table Test

XIONG Aiguo1,JI Jing1,2
(1.School of Civil Engineering and Transportation,South China University of Technology, Guangzhou 510640,China;2.State Key Laboratory of Subtropical Building Science, South China University of Technology,Guangzhou 510640,China)

P315.924

A

1001-8662（2010）04-0017-11

2010-05-06

国家 “十一五”科技支撑计划课题 (2006BAJ04A12)

熊爱国，男，1984年生，硕士研究生.主要从事钢筋混凝土结构抗震性能研究. E-mail：kp20082008@163.com.