复杂网络同步理论在公交调度中的应用

刘兴伟, 张仲荣, 张建刚

(兰州交通大学 数理与软件工程学院,兰州 730070)

复杂网络同步理论在公交调度中的应用

刘兴伟, 张仲荣, 张建刚

(兰州交通大学 数理与软件工程学院,兰州 730070)

针对传统方法优化公交调度难以保证运营效率达到最优的实际情况,基于城市空间结构与交通系统的内在运行机制,构造了城市公交网络模型,利用 N个等同节点的时滞非线性耦合状态方程的同步理论,使公交调度网络系统达到渐进稳定,即各线路乘客达到一种均衡状态。以兰州市公交系统的部分线路为例,验证了该模型及方法的有效性。

公交调度;时滞;复杂网络同步;城市公共交通网络

Abstract:Aimed at seeking an alternative to the conventionalwaywhich fails to ensure bus schedulingwith opt imal operational efficiency,this paper dealswith the development of the urban public transport scheduling network model,based on the urban spatial structure and the transport system of internal operatingmechani sms.The paper introduces the use of the nonlinear simultaneous equation of the coupling state by the same nodeNto realize the asymptotic stability of the entire public transport scheduling ne twork,namely an equilibrium state available for the passengersof the whole bus lines.The paper highlights the part of bus systems which verifies the optional routes of the traveling and the effectiveness of transfer in Lanzhou.

Key words:public transit scheduling;t ime delay;complex ne twork synchronization;urban public traffic network

0 引 言

复杂系统与复杂性研究已成为 21世纪的核心科学问题之一,复杂网络是复杂系统的高度抽象[1]。在复杂网络的同步研究中,汪小帆和陈关荣等[2-3]提出了一个简单的动力学网络模型,还给出了无界区域的同步条件,引起了人们的广泛关注。该模型中各节点相互线性耦合且耦合强度一致,很多学者对其做了进一步地修改和扩展,取得了大量成果[4-5]。

复杂网络理论在交通网络中的应用也有了很大发展,高自友等[6]研究了城市公交网络的无标度特性及度分布指数,以北京市公交网络为例完成了实证分析,并提出了一些今后关于城市交通网络复杂性问题的研究方向[7]。目前,公交调度的研究多集中在车辆的静态调度分析,研究方法主要有数学解析法、概率方法、经验模型、模拟仿真和运筹学等。随着城市规模的不断扩大,这些传统方法遇到了很大的困难而且得不到精确的解。笔者利用时滞复杂网络的同步理论对城市常规公交进行调度,以期达到更优的调度效果。

1 城市公交网络模型构造

城市公交网络由公交站点和公交线路两个基本要素组成,公交线路由若干沿线公交站点连接而成。在实际公交站点中根据线路的拓扑结构可以分为环形线路和直线延伸形线路两种。环形线路的起始与公交站点是同一个站点,一般位于城市的繁华地段,便于换乘;而直线形线路呈直线状,延伸到城市的各个角度。从城市公交网络的公交站点、公交线路和公交换乘的角度考虑,可以构建三种城市公交网络模型。

1.1 公交站点网络模型

公交站点网络模型是以现实的城市公交线路中公交站点之间实际拓扑模型构建的,该模型中公交站点是网络模型的顶点,如果有公交线路 L连接 A点和 B点,且 L沿线的 A、B点中不存在其他的公交站点,则A和B点间有一条边。该模型中顶点的度是通过这一顶点的公交线路的数目,顶点度越大,该顶点越重要,即所谓的枢纽点和换乘站点。

1.2 公交换乘网络模型

评价公交网络的可达性的一个重要指标就是换乘次数。在公交换乘模型中,公交站点是网络的顶点,按照公交线路的走向把线路沿线的站点连接起来。假设在同一条线路上,所有公交站点是全连通的。网络中任一一个站点换乘次数为其之间距离减一。

1.3 公交线路网络模型

公交线路网络模型是以公交线路为顶点,如果两条公交线路之间有部分相同的站点,则这两个顶点之间有一条边连接,如果有多条线路在这两个站点之间相交或部分重合,则这两个顶点之间的权值表示重合线路的数目。网络中权值大的边,在实际网络中就是干线和市区的繁华路段。两点中的O-D流大,就要设置多条公交线路通过。文中利用常规公交线路网络模型建立了时滞常规公交线路调度网络模型。

2 时滞公交网络模型及同步判据

在城市公交系统中,假设该城市有 N条公交线路且不考虑每条线路运行中的交通事故、堵车及车自身等问题。将这N条公交线路抽象成网络中的N个点,这N个点组成一个统一的网络系统。通过对公交网络拓扑结构的分析可得公交网络符合小世界网络的特性[8],由 N个等同节点非线性耦合时滞复杂动态网络模型动力学方程[1]为

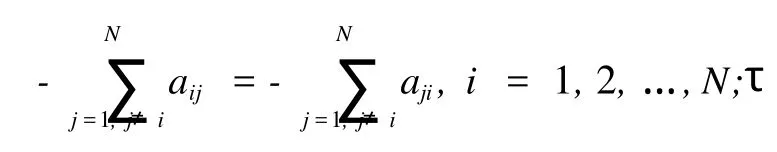
为了判断整个时滞公交网络模型的同步下面介绍一些引理及同步定理[9]。

引理 1式 (1)中定义的不可约分耦合矩阵A=(aij)n×n∈Rn×n,存在一个酉矩阵Φ =(φ1,φ2,…,φN),使得 ATφk=λkφk,k=1,2,…,N成立。式中:λi(i=1,2,…,N)为矩阵 A的特征值。

引理 2假设 H、E和 F为适当维数的实矩阵,且满足 FTF≤I,则对任意标量ε>0,有 H FE+ETFTHT<εHHT+ε-1ETE。如果当 t→∞时,有

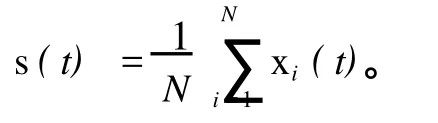
定理 1考虑耦合时滞动态网络系统 (1),设0=λ1>λ2≥λ3≥…≥λN,为耦合矩阵 A的特征值。如果一下N个 n维线性时滞延迟系统关于 0解是渐进稳定的 :η·(t)=(F+ΔF)η (t)+cλkΓ η(tτ),k=1,2,…,N,那么同步状态 (2)是渐进稳定的。

证明 这里令

由引理 1可知,存在一个非奇异矩阵Φ =(φ1,φ2,…,φN)∈Rn×n,使得 ATΦ =Φ Λ,其中Λ =diag(λ1,λ2,…,λN)。因此,使用非奇异转换矩阵 e(t)Φ =η(t)=(η1(t),η2(t), …,ηN(t)) ∈Rn×N,结合式(4)有

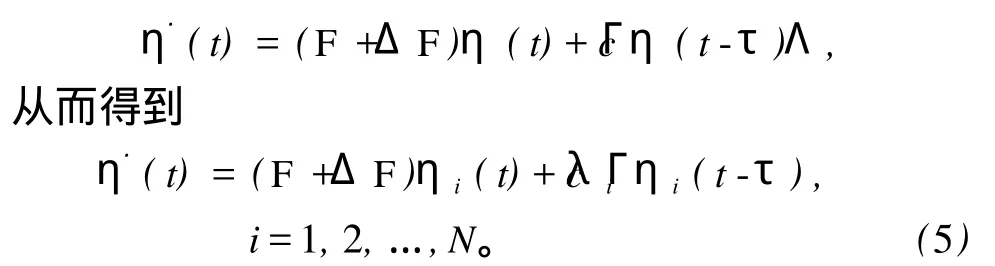
至此,把同步状态 (2)的稳定问题转化为了式 (5)中N个系统的稳定问题,也就是当式 (5)是渐进稳定的,那么 e(t)将渐进趋于零,即同步状态 (2)是渐进稳定的。

3 实证分析

截至 2010年 6月兰州市共有公交线路 104条,423个停靠站点,2 293条连边。数据选取说明:假设在某条线路中,A点可以通达B点,则B点可以通达A点。假设网络中所有公交线路的服务开始时间和结束时间一致而且票价一样。现实中有很多的站点名称相近,在构建的模型中站点名称不一样,即视为不同站点,只要站点名称一致,都视为同一个站点,不论站点距离相近与否。

以兰州市西关什字公交网络为例进行实证分析。经过西关什字的公交线路有 45条,取其中的140、103、138、82四条起始点都在西关什字的线路为研究对象。文中将运用具有时滞的超混沌的Chen系统和 Lü系统对其研究。

这四条公交线路的模型为:

将方程 (6)作为驱动系统,方程 (7)作为响应系统,可以得到时间延迟的误差系统:

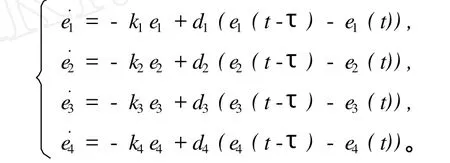
取误差系统中的常数 k1=1,k2=2,k3=3,k4=4,d1=d2=d3=d4=1,当该系统的耦合强度 c为 0.5,时滞τ分别为 5和 10时的同步误差曲线如图 1所示。

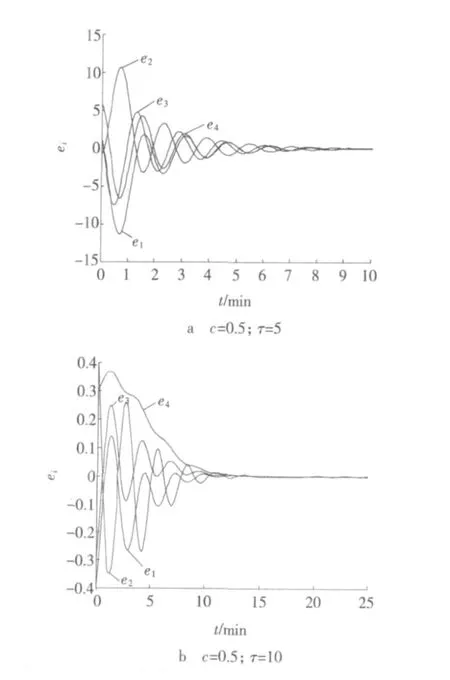
图 1 同步误差曲线Fig.1 Synchron ization error curves

由图 1可知,当时滞τ为 5时,整个系统达到同步速度比τ为 10时快,也就是当调度时间为 5 min时乘客的滞留比较少。

4 结束语

笔者在整个公交网络系统的基础上提出了一种新的公交调度方法,即运用含有时滞的复杂网络的同步理论对城市常规公交进行调度,构造了城市公交调度网络模型。选取非线性的具有时滞的超混沌的 Chen系统和Lü系统对以兰州市西关什字为始发站的四条公交线路进行调度。实证分析证明该方法正确有效,具有广泛的应用前景。

[1] 周 涛,柏文洁,汪秉宏,等.复杂网络研究概述[J].物理,2005,34(1):31-36.

[2] WANG X F,CHEN G R.Synchronization in small-world dynamical networks[J].Int.J of Bifurcation and Chaos,2002,12(1):187-192.

[3] WANG X F,CHEN G R.Synchronization in scale-free dynamical networks:Robustness and fragility[J].IEEE Transon Circuit System,2002,49(1):54-62.

[4] L IC G,CHEN G R.Synchronization in general complex dynamical networks with coupling delays[J].Physical A,2004,343(15):263-278.

[5] ZHOU J,CHEN T.Synchronization in general complex delayed dynamical networks[J].IEEE Transon Circuit System,2006,53(3):733-744.

[6] 高自友,吴建军,毛保华,等.交通运输网络复杂性及其相关问题的研究[J].交通运输系统工程与信息,2005,5(2):79-84.

[7] 高自友,赵小梅,黄海军,等.复杂网络理论与城市交通复杂性问题的相关研究[J].交通运输系统工程与信息,2006,6(3):41-47.

[8] 张 晨,张 宁.上海市公交网络拓扑性质研究[J].上海理工大学学报,2006,28(5):489-494.

[9] WANGQ Y,CHEN G R,LU Q S,et al.Novel criteria of synchronization stability in complex networks with coupling delays[J].PhysicalA,2007,378(2):527-536.

(编辑 王 冬)

Application of complex networks synchronization theory in public transit scheduling

L IU X ingwei, ZHANG Zhongrong, ZHANG Jian’gang
(School ofMathematics,Physics&Software Engineering,Lanzhou JiaotongUniversity,Lanzhou 730070,China)

O231.2;U491.1

A

1671-0118(2010)05-0376-03

2010-07-02

甘肃省自然科学基金项目(3ZS-042-B25-049);甘肃省省属高校基本科研业务费专项项目(620004)

刘兴伟 (1981-),男,河南省开封人,硕士,研究方向:复杂网络理论在交通运输中的应用,E-mail:liuxingwei0001@126.com。