关于不定方程++++=0的一点注记

管训贵

(泰州师范高等专科学校数理系,江苏泰州225300)

管训贵

(泰州师范高等专科学校数理系,江苏泰州225300)

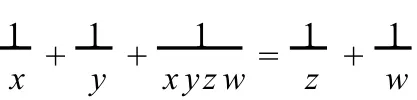
不定方程;正整数解;整除;互素

1 引言及主要结论

L.J.M ordell[1]曾经问:不定方程

的整数解怎样?文[2]根据正负号的讨论,把(1)化为如下三个求正整数解的方程:

并给出了(2)的全部正整数解的表达式.

下面给出定理1、定理2.

定理1 不定方程(3)的全部正整数解可表为

其中n,k,d为正整数,满足

定理2 不定方程(4)的全部正整数解可表为

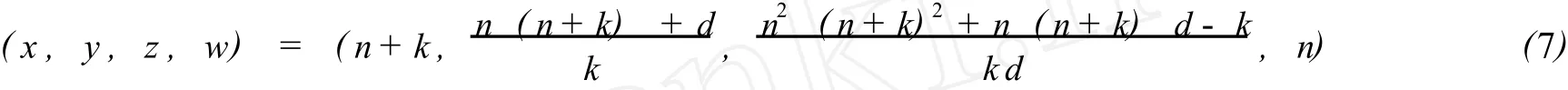
其中n,k,d为正整数,满足

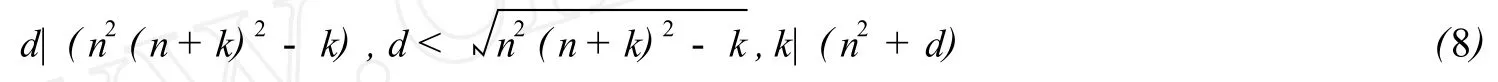
2 定理证明

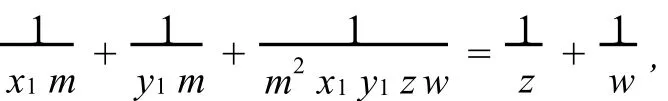
先证定理1.

设w=n,x=n+k,z=y+t,则n,k,t均为正整数.代入方程(3)得

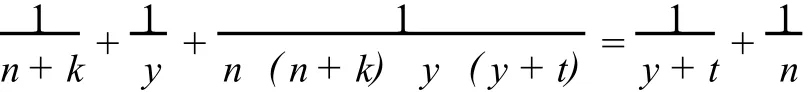
即

要使关于y的二次方程(9)有整数解,其判别式Δ必须是完全平方数.令

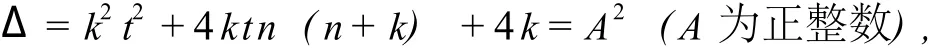
则

因正整数d|(n2(n+k)2-k),所以由(10)式[3-5]有

即

也为正整数.

反之,(5)满足(3),故(5)是(3)的全部正整数解.

再证定理2.

设w=n,x=n+k,z=y+t,则n,k,t均为正整数.代入方程(4)得

即

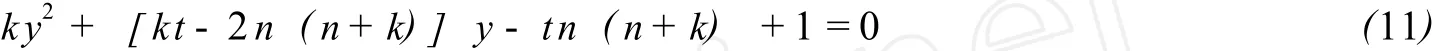
要使关于y的二次方程(11)有整数解,其判别式Δ必须是完全平方数.令

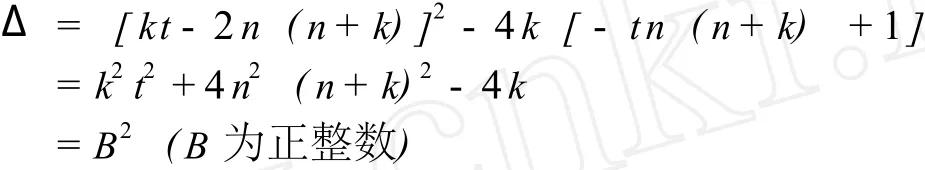
则

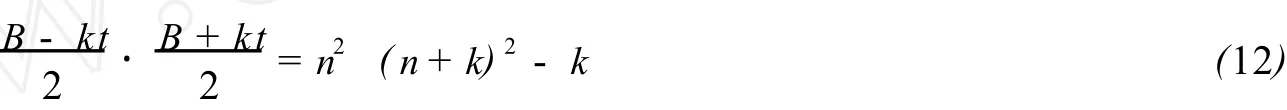
因正整数d|(n2(n+k)2-k),所以由(12)式[3-5]有

即

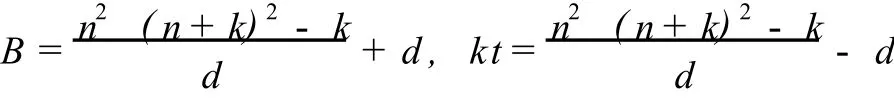
由k|(n2+d)知y为正整数.因此

也为正整数.

证毕.反之,(7)满足(4),故(7)是(4)的全部正整数解.

3 应用举例

若w,x给定,则很容易根据公式(5)、(7)分别求出(3)、(4)的全部正整数解.

例 已知w=11,x=13,试分别求出(3)、(4)的全部正整数解.

解 由n=11,n+k=13知,k=2.因为

所以适合(6)的d只可能是1,7,23,127.代入(5)可得(3)的全部正整数解为(x,y,z, w)=(13,71,10152,11),(13,68,1389,11),(13,60,373,11),(13,8,9,11).又适合(8)的d只可能是1,7,23,127.代入(7)可得(4)的全部正整数解为(x,y,z,w)=(13,72, 10295,11),(13,75,1532,11),(13,83,516,11),(13,135,152,11).

[1]MordellLT.ResearchProblemb[J].CanadMathBull,1973,(17):149

[2]曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989:77-79

[3]管训贵.关于不定方程z2+2(2xy)2=(x2-y2+2xy)2[J].河北北方学院学报:自然科学版,2009,25(01): 14-15

[4]管训贵.不定方程x2-py2=z2的正整数解[J].河北北方学院学报:自然科学版,2009,25(05):5-7

[5]管训贵.关于不定方程x2+(p-1)y2=pz2[J].河北北方学院学报:自然科学版,2010,26(01):12-14

[责任编辑:刘守义]

A Note on Indefin ite Equation++++=0

GUAN Xun-gui
(Department of Mathematics&Physics,Taizhou No rmal College,Taizhou 225300,Jiangsu,China)

indefinite equation;positive integral solution;exact dividing;p rime to each other

O 156.7

A

1673-1492(2010)04-0011-03

来稿日期:2 01 0-0 3-24

管训贵(1963-),男,江苏兴化人,泰州师范高等专科学校数理系副教授.