空气动力对弓网接触压力影响的研究

宋 伟，徐海东

0 引言

近年来，舒适化、高速化是铁路的发展方向。具有高效、重载和对环境污染小等优点的电气化铁路[1]是高速铁路发展的重要途径之一。然而，随着列车运行速度的不断提高，不仅导致列车空气阻力急剧增大、能耗急剧增加，还出现了一系列危及行车安全、降低旅客舒适度和影响周围环境的列车空气动力学方面的问题。

列车在高速运行时，高速气流产生的空气动力影响到高速铁路中受电弓-接触网的受流质量，弓网间的接触压力是评价受流质量和安全运营的重要指标。因此，研究空气动力对弓网接触压力的影响具有重要的实际意义。

本文利用 Matlab软件对动力学模型进行数值仿真，研究了不同运行速度下的空气动力对弓网接触压力的影响，为进一步提高受电弓空气动力性能可采取的措施提供了仿真手段和理论研究基础。

1 受电弓的空气动力学研究

高速列车是在以空气为介质的空间运行，其研究对象可归纳为研究空气流体及在空气流体中的刚体间相互作用力的问题，于是引入了空气动力学理论。

在空气动力学理论中，忽略流体系的分子结构，将流体看作是连续介质，称之为连续性假设或流体介质密度稠度性假设。由于流体的连续性可将运动流体的运动学上的各个基本量（如速度、压力等）看作是某些物理量（如时间、空间坐标）的连续函数，即可对建立在连续函数基础上的数学模型求解空气动力学问题。

按照空气动力学原理[2，3]，受电弓受到的空气动力可分为空气压差力F和空气摩擦力R两大项。前者是受电弓沿运行方向的前后两面所受的空气压力差，这与受电弓前后两面空气的流动有关。后者是由于空气具有粘性，在受电弓滑板和框架的外表面上，因粘附着一层空气阻碍其运动而引起的阻力，称为空气摩擦力。

2 受电弓空气抬升力计算

受电弓在高速运行时，由于受电弓拉杆、推杆和铰链等构件迎风面较小，作用在其上的空气动力也相对较小，所以在计算时仅考虑具有较大迎风面的受电弓上、下臂杆和滑板上的空气抬升力，受电弓为双滑板，上臂按双臂杆计算。

先对受电弓弓头，上臂和下臂进行x，z方向上的空气动力分析，再对整个受电弓进行受力分析。根据列车空气动力学的定义，在通常研究中，定义空气动力系数为Cx，可有：

式中，Fx为受电弓受到的压差力；ν为列车速度；ρ为空气质量密度；A为车头正面投影面积。

对于空气流程中受电弓空气摩擦力大小，可由儒可夫斯基定理求得

式中，Γ为附着涡的强度，V∞为空气来流速度。

2.1 受电弓上下臂杆空气抬升力计算

根据式（1）计算出受电弓上、下臂杆的空气压差力后，得出受电弓运行时作用在受电弓上、下臂杆垂直方向上的空气压差升力（符号上部分表示顺弓；下部分表示逆弓）

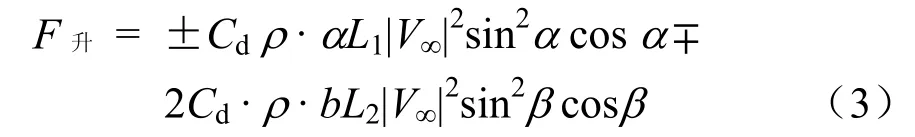
根据式（2）受电弓运行时，作用在受电弓上、下臂杆垂直方向上的空气摩擦升力（符号上部分表示顺弓；下部分表示逆弓）

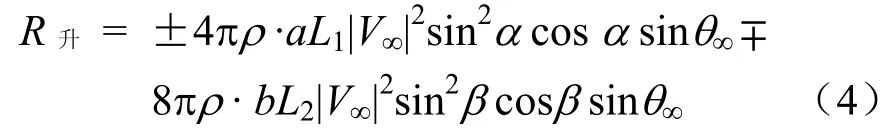
根据公式的计算，得到受电弓运行时，作用在上、下臂杆上的空气抬升力

式（3）—式（5）中，L1为下臂杆的长度，a为上臂杆截面半径，L2为上臂杆的长度，b为下臂杆截面半径，α为下臂杆倾斜角，β为上臂杆倾斜角，θ∞为空气来流的弓角。

2.2 受电弓滑板空气抬升力计算

受电弓滑板在进行绕流计算时，根据文献[2]按平板绕流体处理。由式（1）求得受电弓滑板在垂直方向上的空气压差升力

由式（2）求得受电弓滑板在垂直方向上的摩擦升力

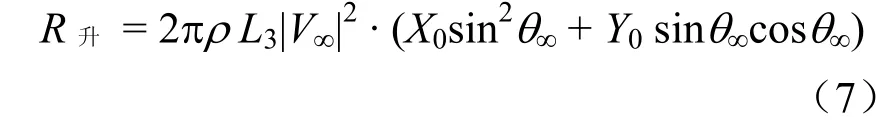
由式（6）和式（7）得到受电弓滑板空气抬升力

式（6）—式（7）中，X0为滑板的宽度，Y0为滑板的厚度，L3为滑板的长度。

3 空气抬升力仿真计算

3.1 受电弓上、下臂杆空气抬升力仿真计算

对于式（3）、式（4），通过在受电弓正下方的机车顶部安装的风向和风速传感器可以测到V∞和θ∞。取L1= 1.5 m、a= 0.025 m、α= 30°，L2=2 m、b= 0.015 m、β= 30°，ρ= 1.293 kg/m3，θ∞在10°左右波动，Cd取 0.7[4]。V∞分别取 70，100 m/s，分别对顺弓和逆弓时受电弓上、下臂杆的空气抬升力进行仿真计算，得到抬升力的波形如图1，图2所示。

由图1可以看出，受电弓在顺弓（闭口）运行时，随着来流速度的增加，受电弓上、下臂杆的空气抬升力会不断增大。当来流速度为70 m/s时，受电弓上、下臂杆的空气抬升力在2 N左右波动，方向向上；当来流速度达到100 m/s时，空气抬升力将达到4.5 N左右，方向向上。

由图2可以看出，受电弓在逆弓（开口）运行时，随着来流速度的增加，受电弓上、下臂杆的空气抬升力会不断增大。当来流速度为70 m/s时，受电弓上、下臂杆的空气抬升力在1.7 N左右波动，方向向下；当来流速度达到100 m/s时，空气抬升力将达到3.6 N左右，方向向下。

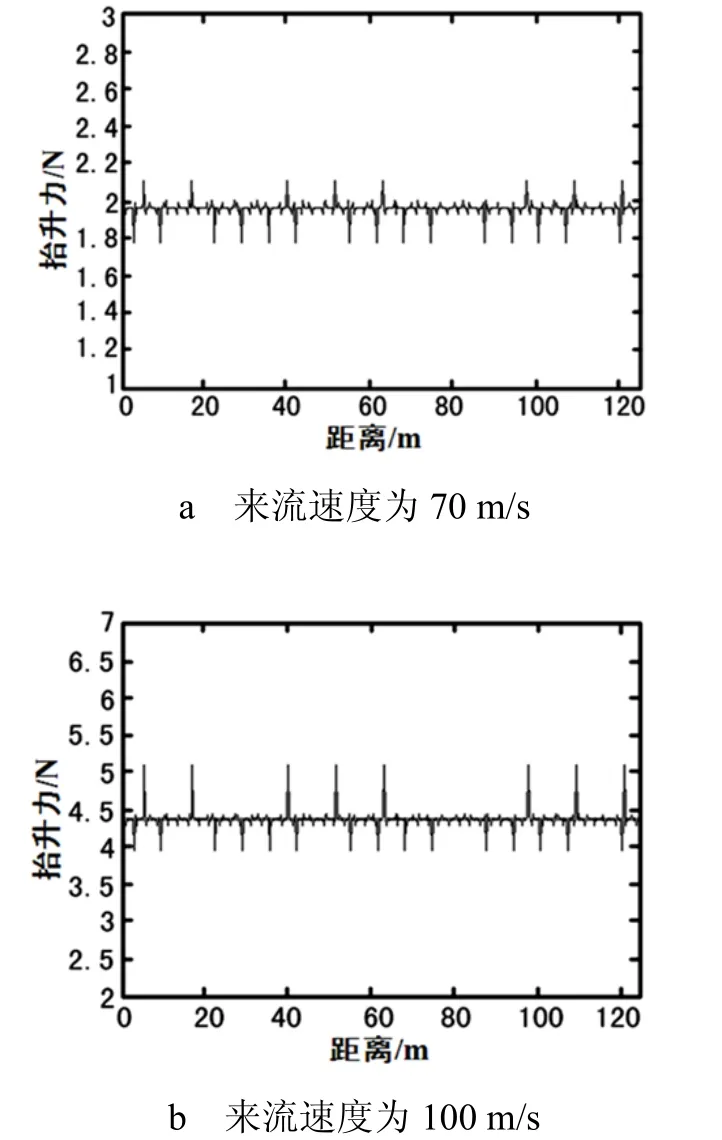
图1 受电弓顺弓（闭口）上下臂杆空气抬升力波形图

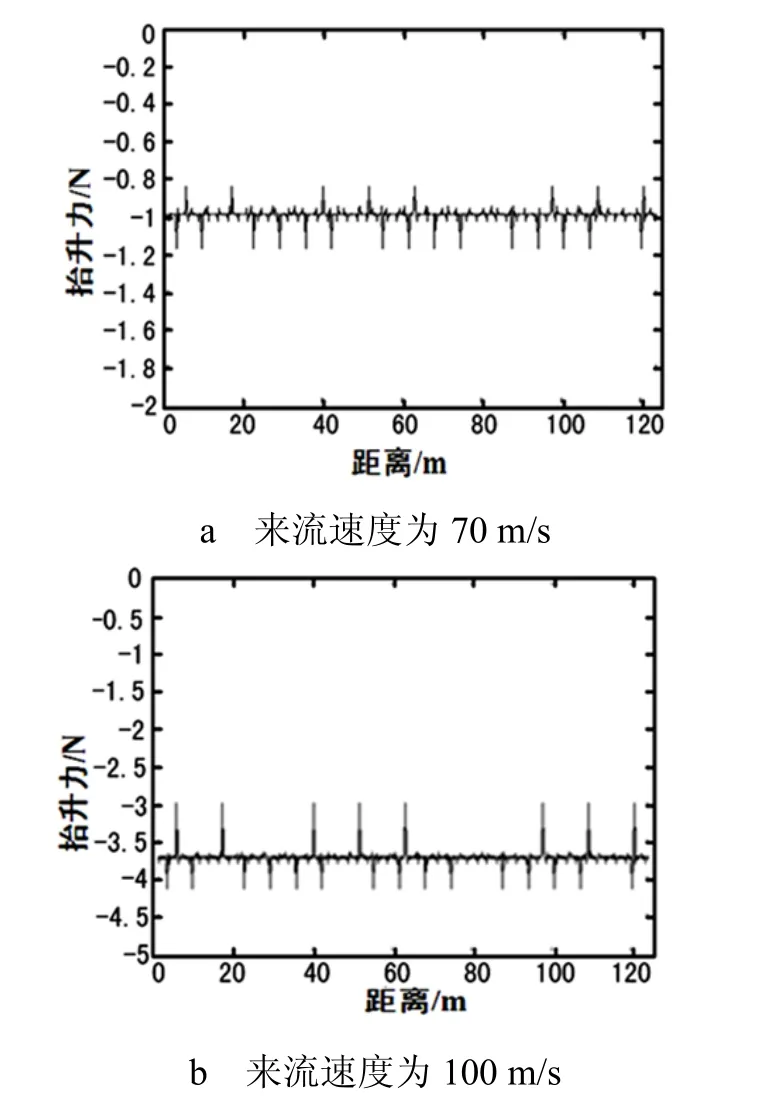
图2 受电弓逆弓（开口）上下臂杆空气抬升力波形图

3.2 受电弓滑板空气抬升力仿真计算

对于式（6）、式（7），取L3= 1.95 m，ρ=1.293 kg/m3，Cd= 0.7[4]，X0= 0.075 m，Y0= 0.075，θ∞在 10°左右波动，V∞分别取 70，100 m/s，用 Matlab软件进行仿真得到抬升力的波形如图 3和图 4所示。

由图3、图4可以看出，随着来流速度的增加，受电弓滑板的空气抬升力会不断增大。当来流速度为70 m/s时，受电弓滑板的空气抬升力在4.1 N左右波动，方向向上；但当来流速度达到较高的100 m/s时，受电弓滑板的空气抬升力将达到8.4 N左右，方向向上。

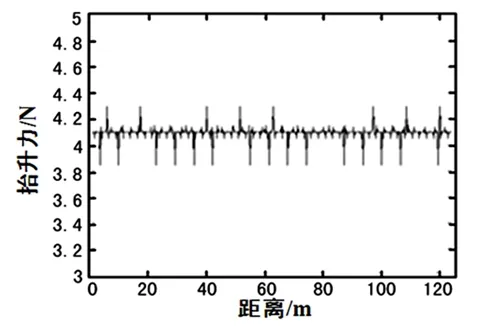
图3 滑板的空气抬升力（70 m/s）波形图

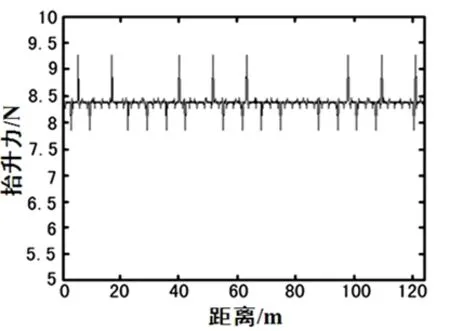
图4 滑板的空气抬升力（100 m/s）波形图

4 结论

本文利用计算机软件对不同运行速度下的空气抬升力进行了仿真及对比分析，得出：

（1）列车高速运行时，受电弓空气抬升力60%～70%作用在受电弓的滑板上，其余部分作用在受电弓的框架结构上。

（2）随着列车运行速度的增加，受电弓空气抬升力增大，与速度的平方成正比，而且随着来流弓角的变化而发生变化。

（3）空气抬升力对弓网接触压力的影响：受电弓逆弓（开口）运行时小于受电弓顺弓（闭口）运行时。

因此，在改善受电弓的空气动力性能时，可以从两方面进行考虑：①减小空气抬升力可在受电弓装有能随上臂杆和弓架间角度变化的导风板。②可装别的零件以承担滑板上的空气阻力；或使受电弓结构更紧凑、减少连接部件数目、杆臂剖面采用流线化设计以及尽量减小迎风面积等气动减阻措施，从而使受电弓滑板始终保持水平位置，并能够减小空气抬升力对接触压力的影响。

[1]于万聚.高速电气化铁路接触网[M].成都：西南交通大学出版社，2003.

[2]易中，吴萱，周丽珍.低速空气动力学[M].北京：冶金工业出版社，2005.

[3]吴子牛，王兵，周睿.空气动力学[M].北京：清华大学出版社，2007.

[4]张弘，于正平.吴鸿标.受电弓空气动力学模型及风洞试验研究[J].中国铁道科学，1995，16（1）：37-49.