基于遗传算法的核电站蒸发器高阶水位模型的降阶方法
2010-09-21谷俊杰米克嵩徐培培
谷俊杰, 米克嵩, 徐培培
(华北电力大学电站设备状态监测与控制教育部重点实验室,保定071003)
对于核电站蒸汽发生器的水位系统,在不影响系统稳定性、响应速度和控制精度等基本要求的前提下,为得到其在特定负载条件下的一般解析式,人们通常使用数学的方法求出较低阶数的模型来近似代替复杂的高阶模型,这对于系统控制参数的选取具有非常重要的理论及现实意义.
大多数实际系统具有时滞特性,用传递函数模型近似实际系统时,辨识出的近似模型一般比原始系统的模型阶次高.如果在降阶模型中人为地引入时滞环节,则可以获得比较满意的降阶模型,但随着模型阶次的变动,待估计参数的个数也发生变化,传统的系统辨识方法并不能较好地适应这种变化,且难以确定系统的时滞[1].核电站蒸发器水位系统是典型的无自平衡线性延迟系统,研究该类系统的有效降阶方法对核电站的仿真试验及模型控制具有一定的现实意义.笔者对本文中的高阶水位模型进行降阶时所采用的遗传算法是一种模拟自然界进化而形成的简单、高效的全局优化算法,在实现高阶线性系统降阶中具有重要的意义.
1 蒸汽发生器的简化数学模型
在对U形管蒸汽发生器进行动态研究时,首先针对文献[2]中的蒸汽发生器简化数学模型(图1)进行仿真.模型参数随负荷变化的对应关系见表1[2].

图1 蒸汽发生器的简化数学模型Fig.1 Simplified mathem aticalmodel of steam generator
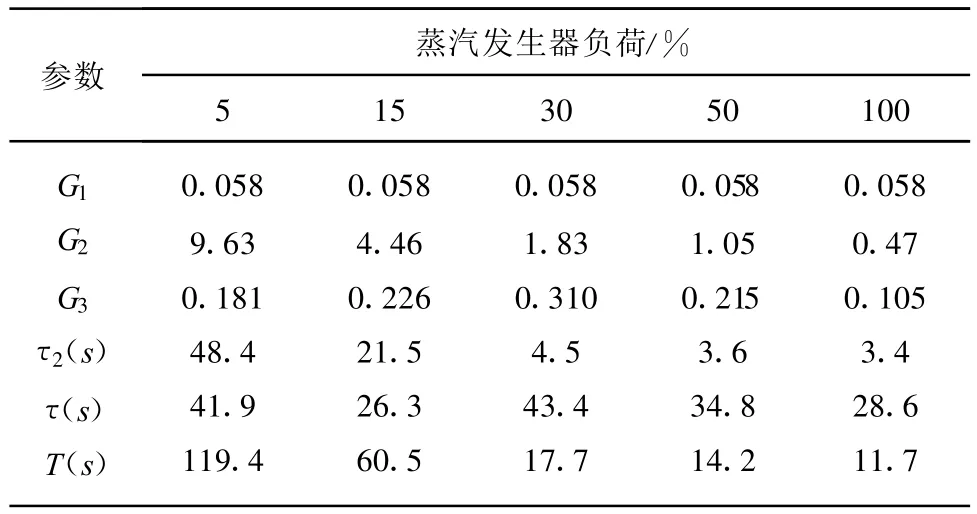
表1 蒸汽发生器模型参数随负荷的变化Tab.1 Steam generatormodel parameters on different loads
图2和图3分别给出了15%负荷和100%负荷下水位的输出曲线.由图2和图3可知,此蒸汽发生器的水位系统为带有惯性延迟环节的无自平衡系统,系统模型为非线性时变模型.
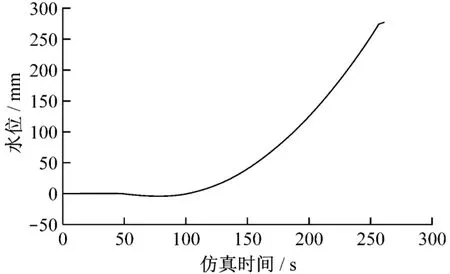
图2 15%负荷下水位的输出曲线Fig.2 The output w ater cu rve on 15%load

图3 100%负荷下水位的输出曲线Fig.3 The ou tputw ater curve on 100%load
2 次最优模型降阶算法
利用次最优化算法进行模型降阶,首先由误差信号e(t)(图4)定义目标函数为J ISE=然后通过参数最优化的方式寻优,找出降阶模型.对目标函数还可以进一步处理,如对误差信号进行加权,引入新的误差信号h(t)=ω(t)e(t),则可以定义新的ISE指标.
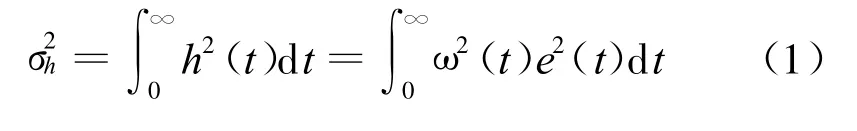
若h(t)为稳定的有理函数,则目标函数的值可以由Åström算法递推或由Lyapuunov方程求解.如果降阶模型或原始模型中含有时间延迟项,则用Åström算法不能直接求解,需要对延迟项采用Padé近似.因为对延迟系统采用近似的最优化算法来求解,所以称之为次最优降阶算法[3].定义待定参数向量 θ=(α1,…,αm,β1,…,βr+1,…,τ),则对一类给定输入信号可以定义出降阶模型的误差信号ê(t,θ),其中误差信号被显式地写成 θ的函数,这样可以定义出一个次最优降阶的目标函数:
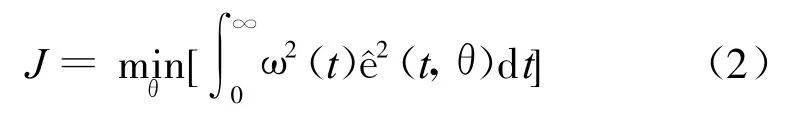

图4 模型降阶误差信号Fig.4 The error signal ofmodel reduction
3 基于遗传算法的模型优化
将遗传算法应用于模型降阶,在一定程度上能够克服传统降阶方法的缺陷,可以较好地实现对降阶模型的优化.
3.1 适应度函数的确定
适应度比例法(又称轮转法)将种群所有的染色体适应度的总和看作一个轮子的圆周,而每个染色体按其适应度在总和中的比例占据轮子的一个扇区.每次染色体的选择可看作轮子的一次随机转动,轮子转到哪个扇区停下来,则该扇区对应的染色体就被选中,尽管这种选择方法是随机的,但它与各染色体适应度成比例.种群中第i个染色体被选中的概率为:

式中:xi代表种群中第i个染色体;f(xi)为第i个染色体的适应度;∑f(xi)为种群中所有染色体的适应度之和.
3.2 优化算法的确定
变异运算用来模拟生物在自然的遗传环境中由于各种偶然因素引起的基因突变,它以很小的概率随机地改变遗传基因的值.在染色体以二进制编码的系统中,变异运算随机地将染色体的某一个基因由1变0或由0变1.若只有选择和交换,则无法在初始基因以外的空间进行搜索,使进化过程在早期就陷入局部解而终止,从而使解的质量受到很大限制.通过变异操作,可以确保遗传基因的多样性,使搜索在尽可能大的空间里进行,避免搜索中失去有用的遗传信息而陷入局部解,从而获得质量较高的优化解[4].
3.3 算法的实现
由于问题比较具体,采用当前在数值计算领域比较流行的Matlab作为编程语言来实现优化算法.
4 仿真结果及分析
文献[2]中15%负荷和100%负荷下蒸汽发生器水位系统的原始传递函数G1(s)、G2(s)为:
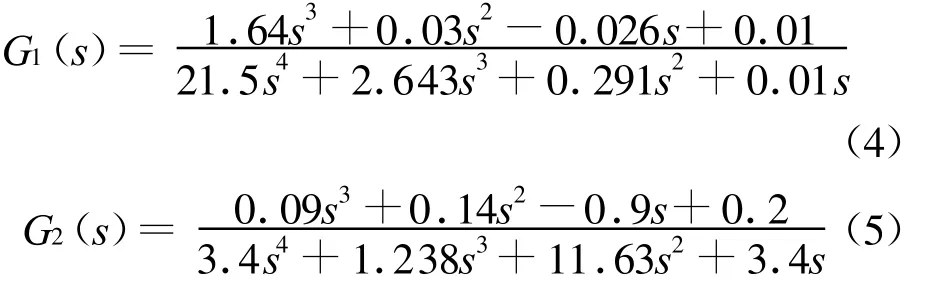
用传统降阶方法得到的二阶近似模型的传递函数 T1(s)、T2(s)为 :

用次最优降阶算法及遗传算法优化后所得的二阶近似模型的传递函数Q1(s)、Q2(s)为:

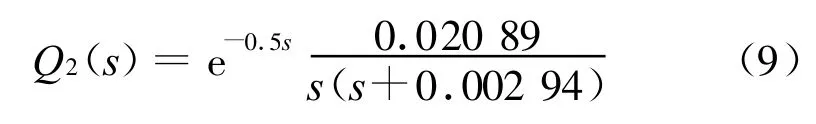
在M atlab平台上分别对上述2种降阶方法得到的传递函数进行阶跃响应仿真,并与原始模型的仿真曲线进行比较.在15%负荷和100%负荷下的仿真曲线分别见图5和图6.

图5 15%负荷下传统算法、遗传算法的降阶曲线与原始曲线的比较Fig.5 Comparison of the traditional algorithm,geneticalgorithm redu ced-order cu rve with the o rginal cu rve on 15%load

图6 100%负荷下传统算法、遗传算法的降阶曲线与原始曲线的比较Fig.6 Comparison of the traditional algorithm,genetic algorithm redu ced-order cu rve with the o rginal cu rve on 100%load
由图5和图6可以看出,2种降阶方法的阶跃响应差别比较明显,传统降阶方法的模型响应与原始模型响应的误差比较大,而基于遗传算法的模型响应误差始终比传统降阶方法的响应误差小,仿真结果表明本文提出的方案可取得较好的效果.
5 结 论
综合使用次最优降阶算法及遗传算法实现了在逐代进化中对模型对象进行全局优化的目的.仿真结果表明:采用次最优降阶算法及遗传算法相结合的方法对高阶系统模型进行降阶,可取得很好的优化结果,对控制系统中控制器设计参数的选取起到很好的参考作用,能够达到工程应用的要求.
[1] 田立国,赵泳.基于遗传算法的高阶控制系统模型降阶方法[J].天津职业技术师范学院学报,2004,14(2):14-16.
[2] 滕树杰,张乃尧,崔震华.核动力装置蒸汽发生器水位的分层模糊自适应控制[J].控制与决策,2002,17(6):933-936.
[3] 薛定宇.控制系统计算机辅助设计——M ATLAB语言与应用[M].北京:清华大学出版社,2006.
[4] 刘福国.双人工神经网络建模及约束条件下的遗传算法优化[J].动力工程,2007,27(3):357-361.
