多类支持向量机在语音识别中的应用

刘潇营, 郑郁正, 李国良

（成都信息工程学院,四川成都 610225）

语音识别是研究如何使机器能够准确地听懂人所说的话,实质就是一种模式识别。是近20年来发展起来的一门新兴学科,是人机通信的自然媒介,具有重要的应用价值。目前,语音识别的方法主要有以下两种:（1）隐马尔可夫模型（HMM）识别算法,这是当前使用较广且发展较成熟的算法,算法通过对大量声音数据进行数据统计,建立识别条的统计模型,然后从待识别声音中提取特征,与这些模型匹配,通过比较匹配分数以获得识别结果。但统计模型的建立需要依赖一个较大的声音库。这在实际工作中占有很大的工作量。且模型需要的存储量和匹配计算的运算量相对较大。（2）神经网络。神经网络是模仿人类大脑神经元所设计的智能系统,具有很强的分类能力。但是由于神经网络具有训练时间过长,训练时容易陷入局部最优化,泛化能力差等缺点,很难转化到实际应用中。[1]

支持向量机（support vector machine）是基于统计学理论发展起来的新的机器学习方法,由Vapnik等人提出[2,3]。支持向量机针对有限的小样本,寻找最少的支持向量,最大化分类间隔,确定最优的分类线等方法提高了泛化能力,减小了经验风险。支持向量机最初是为了解决二分类的问题而设计的。而在实际中很多时候面临的是一个多分类的问题。如何将支持向量机推广到多分类的情况中,很多文献都提出了不同的方法[4]。多类（M-ary）支持向量机[5]即为其中一种,它是多个二分类支持向量机的组合,具有使用向量机数目少,速度快等优点,尤其适用于语音识别实时性的要求。

1 支持向量机的基本原理

支持向量机的原理如图1所示,图中黑白圆圈分别表示两种不同类别。带有斜杠线的圆圈为支持向量。其中H为分类线,在二维空间中,存在多条这种分类线,其中,最优分类线的条件是距离两类样本之间的间隙保持最大,在多维空间中,如果存在一个超平面能够将两类样本准确地分开,且样本距离平面的间隙保持最大,则该平面为最优超平面。H1,H2分别为两类中离H最近的样本且平行于H的直线,它们之间的距离为分类间隔[6]。

设有 n个样本:（xi,yi）,yi∈{-1,1},i=1,2,…,n

当线性可分,对于所有样本存在超平面w◦x+b=0,满足

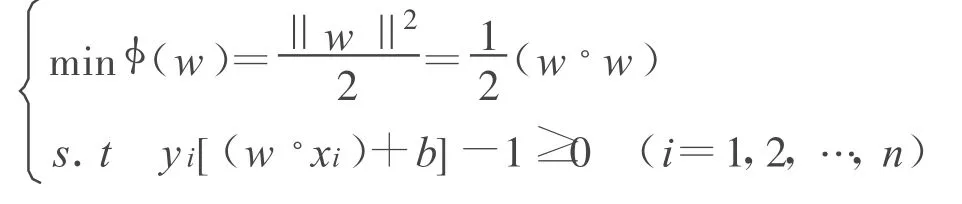
图1 支持向量机原理图

当线性不可分,则需引入松弛变量ζ,满足

C为惩罚因子,为＞0的正数。

K（xi,xj）为核函数。当非线性不可分时,通常将低维空间的数据通过非线性的函数映射到高维空间,再在高维空间内解决分类的问题。如果选取的非线性函数恰当,那么在输入空间内的线性不可分问题可转化为线性可分问题,因此,通常在高维空间的运算中,用核函数取代线性空间中的内积。

决策函数为:

常用的核函数:

（1）线性核函数（linear） K（x,xi）=x◦xi

（2）多项式核函数（poly） K（x,xi）=[（x◦xi）+1]p,p为多项式的阶数。

2 M-ary支持向量机

M-ary支持向量机由Sebald和Buchlew等人在2000年提出。支持向量机多分类使用较多的算法有“一对一”或者是“一对多”[7]。这两种算法的缺点是存在多少种类别就得构建多少个支持向量机,增加了训练的时间,耗费了系统较多的资源。M-ary支持向量机也是由多个二分类器组合而成,从文献[5,8]中得知,在处理 k类问题时,只需要构造log2k个M-ary子分类器。M-ary支持向量机的结构如图2所示。

M-ary支持向量机按照以下规则构造子分类器:

上式中k为分类器的个数,S={1,2,3,…,k}。则原本k分类的问题即转换成log2k类问题。样本集按上式规则分为+1,-1两类。设样本 xi对应的第k个子分类器的输出为y＾k,则样本的最终类别通过以下方程来计算:

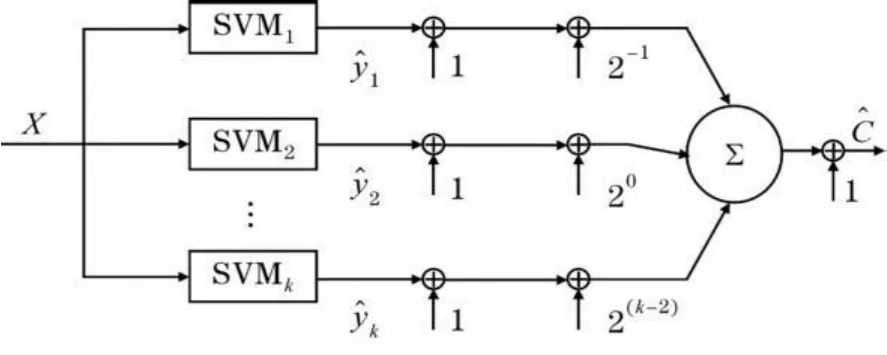
图2 M-ary支持向量机构造图

3 语音特征的提取

要构成一个完整的语音识别系统,除了具备一个优良的识别算法,还需要有相应的前端处理部分才能够进行有效的工作。

从图3得知,要对语音信号进行识别,首先从信号中提取出表征其特征的参数,特征参数的好坏直接影响识别的效果。语音信号是一种时变的非平稳信号,它的频谱特性随着时间的改变而改变,但传统的线性预测倒谱系数（LPC）,美尔倒谱系数（MFCC）都是利用语音信号的短时非平稳特性提取参数,因此,这些方法对于提取有效的语音特征有一定的局限性。

图3 语音识别系统框图

近年来,小波理论发展迅速,被广泛应用于信号的处理与分析中。小波变换能够很好的表征以低频信息为主的信号,但是对于高频信息较多的信号,不能很好地分析其细节信息。小波包理论是一种非平稳信号的分析方法,是小波分析的推广,继承了小波变换多分辨率的思想,非均匀的划分时频空间,对频带进行多层划分,将小波变换没有细分的高频部分进行更为详细的分解,更有利于对包含大量中、高频信息的信号进行时频局部化的分析。这些特点使小波包分析方法有别于传统的语音处理中的短时傅立叶分析方法。

由于人耳对语音信号的感知是非线性的,比较敏感的区域集中分布在24个频带,称为临界频带[9]。MFCC参数的提取就是根据这24个频带构建了24个带通滤波器,将其输出的对数能量再进行DCT变换得到。小波包提取信号特征参数也是根据相同的原理,在小波包分解结束后,选取处于这24个频带上的小波包频带结点,计算其对数能量再进行DCT变换。

小波包提取特征参数的过程如下:

（1）对语音信号进行预加重,消噪,分帧,加窗。分帧是为了提高特征参数的精度。

（2）对每帧信号进行小波包分解,并且计算对应临界频带的结点小波系数的对数能量。

其中 WPXk,m为第k个子带的第m个小波系数,Nk为第k个子带的小波系数的个数,K为所选频带的频带编号。

（3）对Sk进行DCT变换,得到新的特征参数

p为特征参数的维数。

4 仿真结果

实验的语音数据均由11250Hz采样,16bit量化,在实验室环境下录取5位男生和5位女生的声音,分别读取10个单词,每个单词阅读10遍,总共采集1000个样本。其中500组作为训练样本,500组作为验证样本。数据按照帧长256点,帧移128点分帧。采用小波包提取出特征系数,小波函数为‘DB6'。进入M-ary支持向量机进行处理,支持向量机的核函数分别选取‘linear',‘poly',‘rbf'核函数进行比较。

为了使语音识别系统显得直观、实用,实验在MATLAB环境下构建了GUI界面,如图4、5所示,方便查看识别效果。

通过该GUI界面分为训练和识别两部分,训练部分主要是将训练集的特征参数输入至M-ary支持向量机中,寻找支持向量,求取拉格朗日乘子,将训练结果保存为.mat文件。识别部分通过load.mat文件的方式获取训练后的数据,再将此数据应用于需要进行识别的声音,判定其所表征的含义。使用者可以自由的选定训练模板的个数,在识别部分也可以选择需要比较的模板的范围。这样可以提高识别效率,减少识别时间,提高系统的实时性。

为了选取最佳核函数,分别对‘linear',‘poly',‘rbf'的分类结果进行了比较,结果见表1。

图4 训练界面

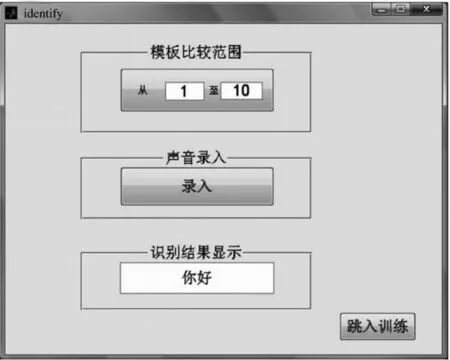
图5 识别界面

表1 分类结果比较图

从表1中得知,‘rbf'核函数的分类效果最佳,‘linear'函数分类效果较差。因为‘rbf'核函数具有较强的非线性的特性,将低维空间的数据能够更好地转换到高维空间进行线性划分。在接下来的实验中,M-ary支持向量机都选定‘rbf'为其核函数。

为了比较识别效果,分别运用了BP网络、SVM、M-ary SVM 进行语音实验,实验结果见表2。

表2 实验结果1

从表2可以看出M-ary支持向量机的识别效果最好,SVM居中,BP网络效果最差,且M-ary SVM所用的训练时长最短,比SVM快了一半,那是因为与SVM 相比,M-ary的子分类器个数大为减少,所以训练时间最少,而且精度也最高。为了充分验证M-ary支持向量机的抗噪能力,即强健性。在训练样本中混入零均值的高斯白噪声,测试样本不变,此时信噪比为30dB。重新训练支持向量机,此时这3种识别方法的抗噪测试比较结果见表3。

表3 实验结果2

从表3可看出混入高斯白噪声后,对训练的时长影响不大,但对识别率都有一定的作用。BP网络受噪声干扰的影响最大,而SVM和M-ary SVM受的影响较小,识别率改变的幅度不大。这是因为SVM采用的是将数据从低维空间映射到高维空间的思想,由支持向量来决定最优分割线,由于噪声的能量不大,加入的高斯白噪声在低-高维转换时,能起决定性影响的数据大量减少,所以,支持向量机的抗噪声能力优于BP网络,并且性能稳定。M-ary SVM的识别率和抗噪能力都是最优的。

5 结束语

介绍了M-ary SVM在语音识别系统上的应用,并引入BP网络和标准SVM对其分类效果进行比较。从仿真结果看,M-ary SVM具有较为理想的分类能力,其抗噪能力也优于BP网络和标准的SVM。但是M-ary SVM的识别正确率受样本选取的影响较大,具有一定的局限性,希望在今后的研究中会得到进一步的改进与优化。

[1] 詹新明,黄南山,杨灿.语音识别技术研究进展[J].现代计算机,2008,（9）:43-45.

[2] 张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26（1）:32-42.

[3] Vapnik.The nature of statistical learning theory[M].New York:Spinger-verlag,1995.

[4] 张宏烈.支持向量机在字符识别中的应用研究[J].微计算机信息,2006,11:245-247.

[5] Daniel J Sebald,James A Bucklew.Support Vector Machines and the Multiple Hypothesis Test Problem[J].IEEE TRANSACTIONS ON SIGNAL PROCESSING,2001,49（11）:2865-2872.

[6] 肖健华.智能模式识别方法[M].广州:华南理工大学出版社,2006:148-155.

[7] 余辉,赵辉.支持向量机多类分类算法新研究[J].计算机工程与应用,2008,44（7）:185-189.

[8] 肖燕彩,陈秀海.改进的M-ary支持向量机模型及其在变压器故障诊断中的应用[J].上海交通大学学报,2008,42（12）:2033-2036.

[9] 韩纪庆,张磊,郑铁然.语音信号处理[M].北京:清华大学出版社,2004:25-31.

[10] 飞思科技.小波分析理论与MATLAB7实现[M].北京:电子工业出版社,2005.