PSO-BP组合人工神经网络算法研究
2010-09-20高峰
高峰
(山西大同大学工学院,山西大同037003)
PSO-BP组合人工神经网络算法研究
高峰
(山西大同大学工学院,山西大同037003)
基于梯度下降的BP人工神经网络应用广泛,但网络目标函数误差曲面极其复杂,网络初始值的选取对网络训练结果影响很大,导致收敛速度慢,容易陷入局部极小等问题.基于粒子群算法(pso)的训练方法能够摆脱陷入局部最优的困扰,但粒子群算法局部搜索能力不够,影响网络的训练效果,在充分研究两种算法特点的基础上,提出一种新的组合训练方法,建立了PSO-BP组合人工神经网络模型.
组合人工神经网络 BP算法 PSO算法 算法设计
人工神经网络(ANN)以大脑生理研究成果为基础,模拟生物神经网络信息处理的网络,是传统工程系统与人工智能领域处理技术的混合,通过学习、记忆,采用类似黑箱方法拟合输入变量与输出变量间的非线性关系[1,2],具有自学习、自组织、自适应能力和非局域性、非定常性、非凸性、非线性动态处理等特点,宜于表现多影响因子间的复杂因果规律,是求解非线性问题的常用方法.传统BP网络初始权值、阈值随机设定,初值选取不当直接影响网络收敛性能和最终稳定状态,网络学习易陷入局部极小,存在收敛速度慢、训练时间长等问题,不能保证所优选权值为全局最优.
自然界中单个自然生物通常不是智能的,但却有一定的群体行为,即整个群体表现出处理复杂问题的能力.基于对鸟群捕食行为研究和演化计算理论[4]的粒子群优化算法(PSO),就是模拟自然生物行为的优化技术,具有记忆粒子最佳位置的能力和粒子间信息共享的机制,通过种群间内个体合作与竞争可实现优化问题求解.为克服传统BP神经网络缺陷,本文将PSO算法与BP神经网络结合,建立PSO-BP组合人工神经网络模型,以充分发挥PSO算法全局寻优能力和BP算法局部搜索优势,缩短训练时间,克服连接权值随机问题.
1 BP-ANN理论
人工神经网络(ANN)理论[1,2]是上世纪80年代中后期发展起来的非线性科学,在大脑神经网络认识的基础上,人工构造的能实现某种功能的神经网络,是理论化的人脑神经网络数学模型.ANN由许多神经元组成并行分布结构的信息处理网络,显示出人脑的某些基本特征,是传统工程系统与人工智能领域处理技术的混合;它可从积累的工作经验中学习知识,在数据含噪音、缺项或缺乏认知时能获得较为满意的结果,对于多变量系统,泛化能力强,能逼近任意非线性映射;高度并行计算能力使得容错能力更高.
ANN模型结构是决定网络特性的第二大因素,大量神经元按一定规则连接形成一定的拓扑结构,根据神经元连接方式与内部信息传递方向的不同,可分为前馈型神经网络和反馈型神经网络.ANN能进行复杂的逻辑操作和非线性映射,依赖于神经元间的相互作用,知识或信息存储表现为网络元件之间的分布式的物理联系.生物神经元信息传递特性的数学表达式为:

式中,xi-输入信号;wi-连接权值;Σ-信号累加;θ-神经元阈值;f-传递函数;Yi-输出信号.
传递函数是神经元、神经网络的核心,反映神经元输出与激活状态间的关系,决定了神经网络求解问题的能力与效率,可分为阈值型传递函数、分段线性传递函数、非线性传递函数,见图1.
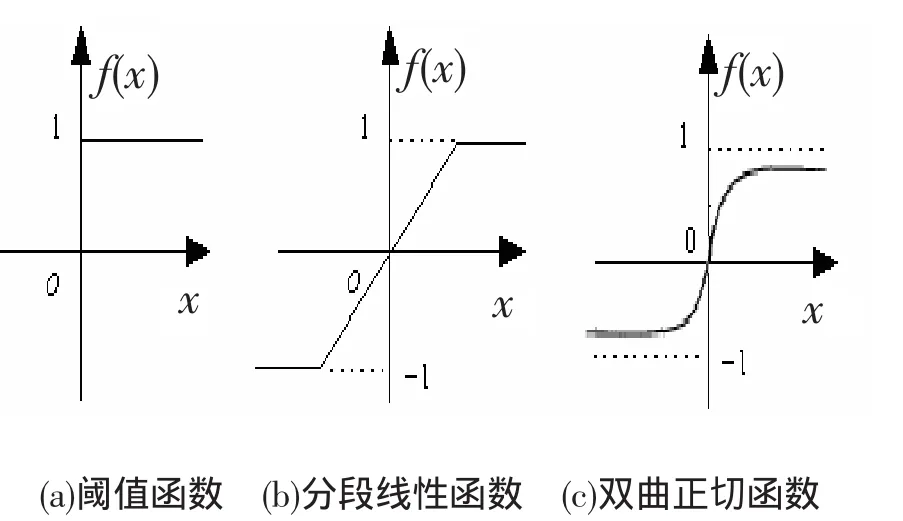
图1 人工神经元中的传递函数
1.1 BP神经网络原理
Ramelhart等提出的误差反传训练(BP)算法[1,2]由正向计算和误差反传两部分组成.BP神经网络包含一个输入层、一个输出层及至少一个隐含层,见图2.在网络的正向计算中,输入信息从输入经隐含层逐层处理,并传向输出层,在正向传播的过程中,每一层神经网络的状态只影响其下一层神经元的状态.若输出层不能得到期望的输出,则转入反向传播,将输出误差沿原来的连接通路返回,通过修改各层神经元的权重,使最终的输出误差达到最小.
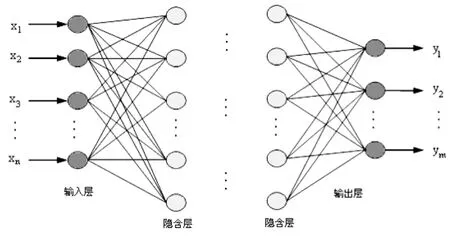
图2 BP人工神经网络模型结构
隐含层神经网络是一组从输入节点到输出节点的高度非线性映射,BP累积误差反向传播算法步骤:①确定BP神经网络结构;②设置权值、阈值矩阵、学习速率和动量因子;③学习训练,直到误差足够小.BP算法数学意义明确、步骤分明,并具有中间隐含层和有相应的学习规则可循,使得它具有对非线性模式的识别能力,已成为工程应用最多、最成熟的方法之一.
1.2 BP人工神经网络参数
1)神经网络层数
Kolmogorov定理:任意连续函数f∶RT→Rm,f可以精确地用三层前馈网络来实现.选择合适神经元,神经网络可任意精度逼近任一连续函数.增加层数可降低误差、提高精度,但网络趋于复杂,从而增加了网络训练时间[3],见图3.因此,BP神经网络设计时,一般设置一个隐层,先考虑增加隐含层神经元数,当节点数很多仍不能改善网络性能时,才考虑增加隐层.
2)隐含层神经元数
较小规模网络学习比较困难,适当增加神经元数目可提高误差精度,训练效果易于观察和调整.但隐层节点数过多,节点冗余增加网络训练时间,模型泛化性能降低.通常可采用构造法、进化法、删除法等确定隐层神经元数目.
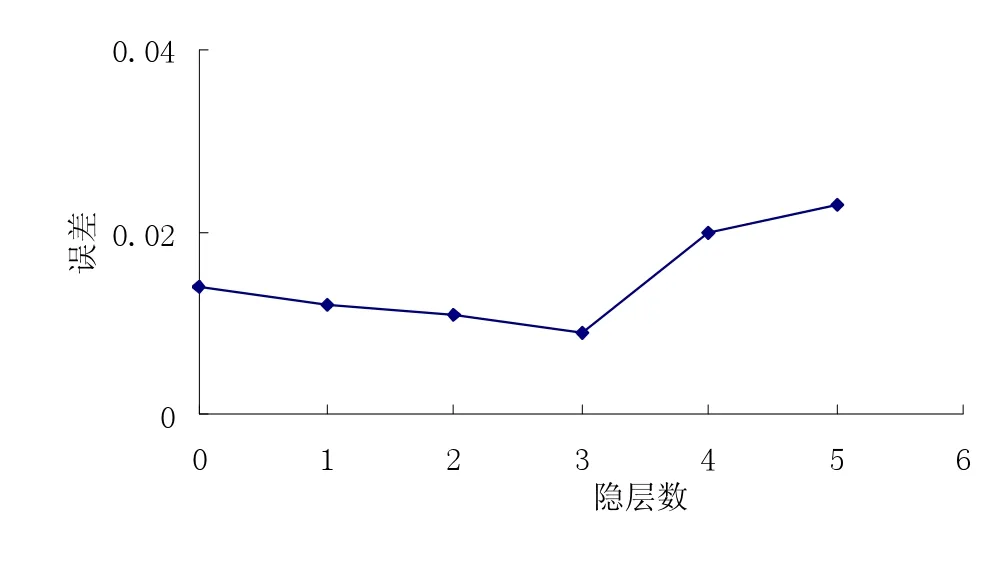
图3 系统误差-网络隐层数变化曲线
3)初始权值
初始权值决定了非线性系统的收敛性及收敛速度.初值太大,使得加权后的输入、输出值落在S型传递函数饱和区,导数太小,导致计算权重修正值趋于0,从而使得调节过程几乎停顿下来.因此,初始加权的神经元输出值应近于零,以保证神经元权值在传递函数变化最大处调节,常取(-1,1)间的随机数.
4)学习速率
学习速率决定每一循环训练中权值变化量,值过大可导致系统不稳定,值过小虽能保证跳出网络误差表面低谷,趋于误差最小值,但收敛速度慢,效率低.一般在[0.1,0.8]之间取值即可保证系统稳定性和精度要求.
2 粒子群优化算法
Reynolds研究鸟群飞行发现,鸟仅追踪它有限数量的邻居,但最终结果是整个鸟群好像在一个中心的控制下,即复杂的全局行为是由简单规则的相互作用引起.一群鸟在随机搜寻食物,若某区域里只有一块食物,那么找到食物最简单有效的策略就是搜寻目前离食物最近的鸟的周围区域.
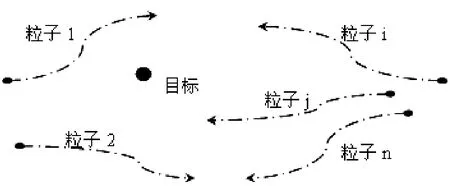
图4 粒子群算法原理示意图
Eberhart和Kennedy从中得到启示,将鸟类寻找食物与特定问题寻找最优解联系起来,用粒子(质量、体积忽略不记)来代替飞鸟,并为粒子制定类似于鸟类运动的简单行为规则,从而使整个粒子群的运动表现出鸟类觅食的特性,即粒子最终能够飞向解空间的最优解处[4-6],见图4.
PSO求解优化问题时,解空间初始化为一群随机粒子,每一粒子都有自己的位置、速度以决定飞行方向、距离,还有一个由被优化函数决定的适应值.各粒子记忆、追踪当前的最优粒子,在解空间中搜索.在每次迭代中,粒子通过跟踪个体极值、全局极值更新自己的速度、位置.粒子速度和位置更新方程为:
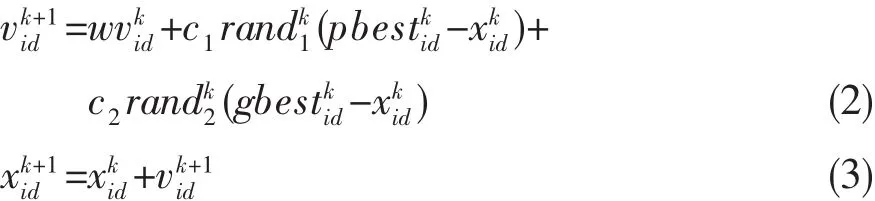
PSO算法采用速度-位移模型,避免了复杂的遗传操作,特有的记忆使算法可动态跟踪当前的搜索情况来调整其搜索策略,算法简单有效,应用领域已扩展到多元函数与参数优化、模式识别、聚类分析、神经网络等[4].
3 PSO-BP组合人工神经网络算法
3.1 BP神经网络与PSO融合
BP模型不需精确数学表达式,只要用已知模式对网络加以训练,网络就具有输入-输出间的映射能力;理论基础坚实、推导过程严谨、物理概念清晰、通用性强,广泛应用于模式匹配、分类、自动控制等领域.但BP算法基于梯度下降算法,本质上属局部寻优算法.复杂网络的误差曲面是一高维空间中的曲面,非常复杂和不规则,局部极小点多,见图5,一旦陷入就很难逃脱出来,学习效果变差.
PSO算法以生物群体内通过个体间的合作与竞争所产生的群体智能为核心理论体系,属于全局优化算法,具有收敛速度快,操作简单、易于编程实现,是一种良好的优化算法.因此,引入粒子群算法对BP网络初始权值和阈值等参数优化,可产生一种新的组合人工神经网络模型.
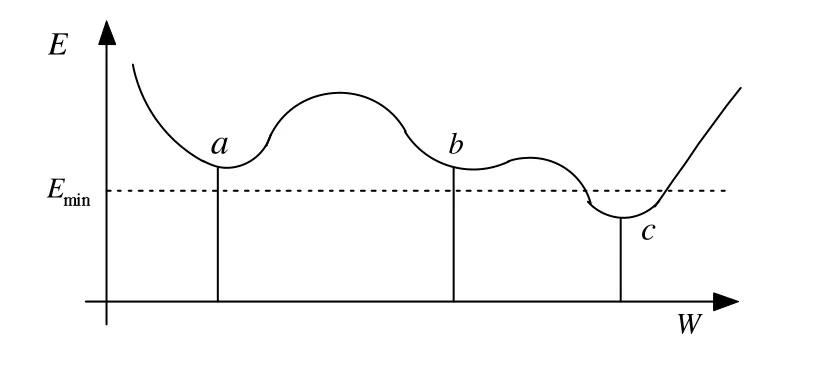
图5 单权值调整过程中的局部极小点
PSO-BP神经网络基本原理是,先将神经元间所有连接权值编码成实数向量以表示种群中个体,随机生成向量群体,迭代中新生成的个体向量还原为神经网络权值,将训练中产生的均方误差作为评价个体的适应度函数,此时训练转化为寻找一组使均方误差最小的最佳联接权值优化问题.若均方误差小于系统设定值或迭代次数大于最大迭代次数,则训练过程停止;否则,迭代继续进行,直至最大迭代次数,此时参数组合已较接近于最佳组合.然后,采用BP算法进一步精确优化上面得到的网络参数,直至网络参数最优.这样既提高了神经网络的学习能力,又增强了神经网络泛化性能和预测能力.
3.2 PSO-BP组合人工神经网络算法流程
PSO-BP组合神经网络算法流程如下:
1)初始化BP神经网络结构,设定网络的输入层、输出层的神经元个数,设置网络参数,通过试算确定最佳隐含层神经元个数.
2)初始化粒子群的规模、维度D以及每个粒子的初始速度、位置.种群规模一般取为10~40间的数值,复杂问题大于100;初始速度、位置可随机赋值.问题解空间维度D计算公式:

式中,m、n、p、q分别为输出层-隐含层连接权值个数、隐含层-输出层连接权值个数、隐含层阈值个数、输出层阈值个数.
3)根据适应度函数计算每个粒子的适应度方差,步骤为:
①按当前网络结构和权值、阈值计算出每个样本的输出值.
②计算每个训练样本的输出值的误差.
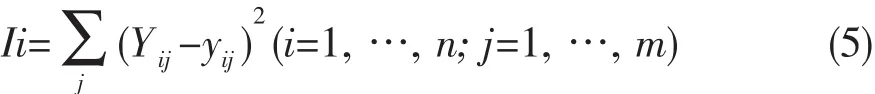
式中,n-训练集样本总数;m-输出层神经元个数;Yij-实际输出值;yij-理想输出值.
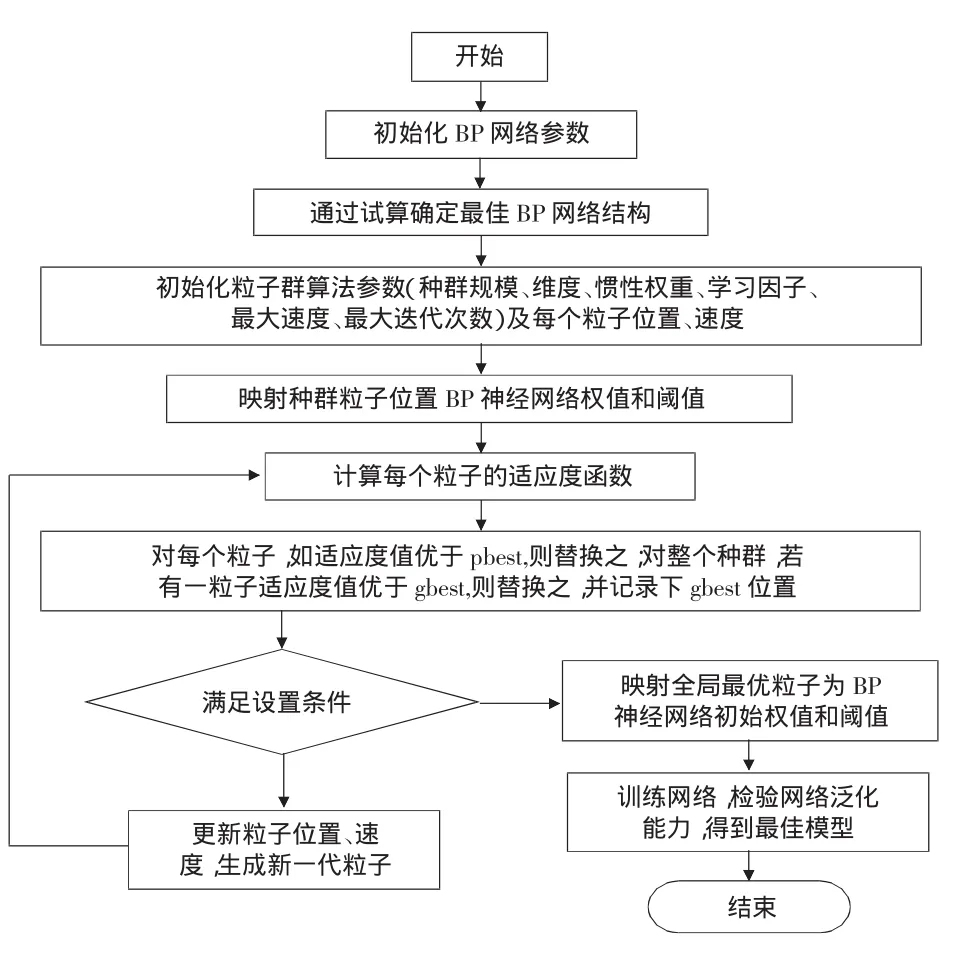
图6 PSO-BP组合神经网络运算流程
③计算出该粒子的适应度方差.

4)更新每一个粒子的个体极值、全局极值,生成下一代粒子.惯性因子w设计为随迭代次数递减,按照式(7)进行自适应调解.
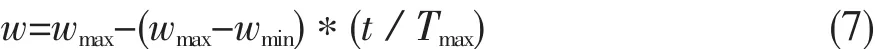
式中,wmax-最大惯性权重;wmin-最小惯性权重;t-当前迭代次数;Tmax-最大迭代次数.
5)检查粒子适应度方差和当前最大迭代次数,若误差大于系统设定值或迭代次数小于最大迭代次数,继续步骤(3)进行下一代粒子计算;否则,退出迭代计算,将全局最优粒子位置映射为网络初始权值和阈值,见图6.
4 结论
BP算法非线性模式识别能力强大,但存在网络学习易陷入局部极小,收敛速度慢、训练时间长等问题.PSO算法以群体智能为核心理论体系,收敛速度快,操作简单、易于编程实现,是一种很好的全局优化算法.基于粒子群算法建立的PSO-BP组合人工神经网络模型,充分利用神经网络的学习能力,发掘数据内隐藏的规律,为进一步拓展人工神经网络应用领域开辟了一条新的途径.
[1]张良均,曹晶,蒋世忠.神经网络实用教程[M].北京:机械工业出版社,2008:12-45.
[2]徐秉铮,张百灵,韦岗.神经网络理论与应用[M].广州:华南理工大学出版社,1994:2-16.
[3]冯夏庭.智能岩石力学导论[M].北京:科学出版社,2000:102-145.
[4]Bonabean E,Dorigo M,Theraulaz G.Inspiration for optinization from social insect behavior[J].Nature,2000,406(6):39-42.
[5]曾建潮,介倩,崔志华.微粒群算法[M].科学出版社,2004:52-85.
[6]杨威,李岐强.粒子群优化算法综述[J].中国工程科学,2004,6(5):87-90.
Abstract:BP artificial neural network based on gradient algorithm method is widely applied,but because the error surface of object function is extramly complex and the choose of initial value effects network training results,convergence rate is slow and local minimum is likely to fall into.Paticle swarm optimization algorithm has better global searching ability to get rid the puzzles of falling into local minimum.By adequately studying on the two algorithms'characteristics,a new type of combined artificial neural network training method is put forward,and PSO-BP ann model is successfully built.
Key words:combined artificial neural network;bp algorithm;pso algorithm;algorithm design
〔编辑 石白云〕
Research of PSO-BP Combined Artificial Neural Network Method
GAO Feng
(School of Engineering,Shanxi Datong University,Datong Shanxi,037003)
TP183;TU452
A
1674-0874(2010)03-0066-04
2010-04-12
高峰(1977-),男,山东泰安人,讲师,博士,研究方向:工程力学与岩土工程.
