水下航行器纵向运动的非线性自适应反演控制＊

张 宁

（西北工业大学航海学院，西安 710072）

0 引言

水下航行器的空间运动模型具有多变量、高度非线性、强耦合等特点，其流体动力学参数很难精确测得，要求控制系统必须具有一定的鲁棒性和自适应能力［1］。滑模控制是提高水下航行器控制系统鲁棒性的重要方法，但在未知参数的情况下，滑模控制需要施加较大的控制输入以克服参数不确定性，对舵机的动态性能有较高要求。

反演设计方法是一种基于Lyapunov稳定性理论的非线性控制递推设计方法［2］，针对具有严格反馈形式的非线性系统，从系统的输出向控制输入“反演”，得到一系列系统化的反馈控制律和相应的Lyapunov函数，实现系统的全局渐近稳定控制。针对含有参数不确定性的系统，通过引入参数自适应机制，在线估计未知参数，构成自适应反演控制，保证了控制的稳定性和对未知参数的自适应性。

文中针对水下航行器纵向运动控制中的参数不确定问题，采用自适应反演设计方法，在线估计未知参数，理论分析和仿真研究验证了该控制器的稳定性和自适应性。

1 水下航行器纵向运动模型

水下航行器纵向运动三阶非线性运动模型［3］可以表示为：

其中：z为水下航行器的航行深度，u为前向速度，w为垂向速度，θ为俯仰角，q为俯仰角速度，Iy为绕y轴的转动惯量，M˙q＜0为流体附加转动惯量，Mqq＜0为流体二次阻尼系数，Mδ为水平舵的俯仰力矩系数，G为重力，xG为重心到载体坐标系原点的距离。

对模型（1）作如下假设：

假设1：状态变量z、θ、q及u、w均可以测量，并且考虑到u和w 的慢变特性，假定˙u＝˙w＝0。

假设2：u cosθ＋w sinθ＞0。

一般情况下，对于巡航式水下航行器有u≫w，θ为一小角，假设2是成立的。

将式（1）中的第3式写为标准形式：

2 自适应反演纵向运动控制器设计

纵向运动控制的目标是：给定常值参考深度信号zd，设计跟踪控制器，使深度跟踪误差z－zd渐近收敛到零，并对俯仰角动态特性中的未知模型参数具有自适应性。

定义新的状态变量｛z1，z2，z3｝：

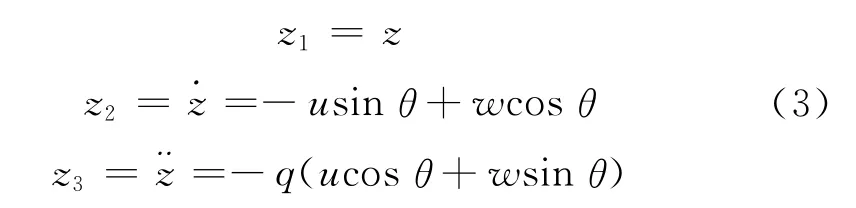
于是方程（1）转换为：

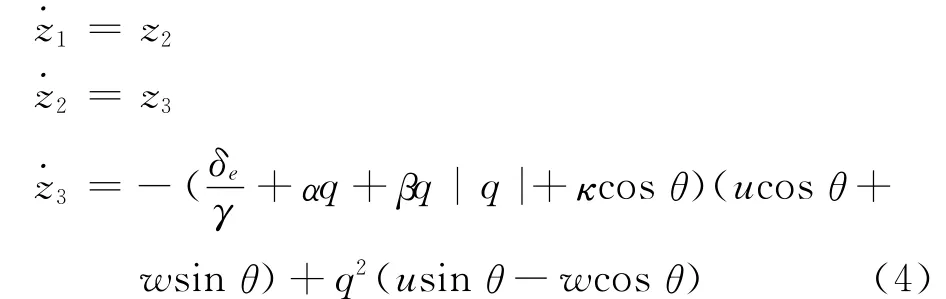
首先定义深度跟踪误差：

zd为常值深度指令，有：

以z2为虚拟控制量，由定义（3）显然有考虑到速度的有界性，其参考轨迹即镇定函数必须具有饱和特性，满足z2的幅值限制［4］，这里取：

其中，λ1＞0、1≥μ＞0为设计参数。定义跟踪误差：

为了使深度跟踪误差e1在后面的反演设计过程中的交叉项影响是有界的，避免对控制输入产生较大的影响，定义Lyapunov函数：

其中，λ2＞0为设计参数。定义跟踪误差e3＝z3－α2，代入式（13）有：

其中，W2（e1，e2）＝W1（e1）＋λ2e22≥0，正定。

定义第三个Lyapunov函数：

以z3为虚拟控制，取镇定函数：

其导数为：

考虑到参数γ、α、β、κ的不确定性，取控制输入：

其导数为：

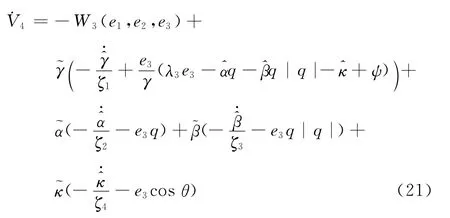
为消除参数估计误差对系统稳定性的影响，设计如下自适应律：

其中，ζ1、ζ2、ζ3、ζ4为自适应参数。代入式（21）得到：

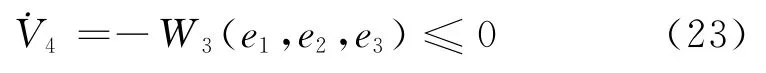
由于V4≥0，信号均有界，根据Barbalat引理，有：

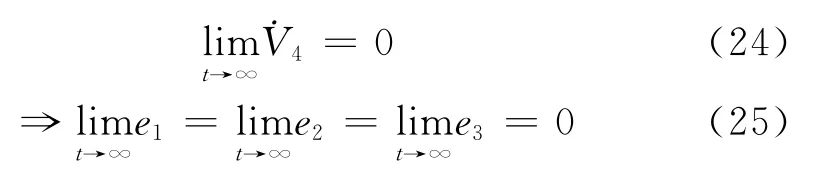
于是得到下面的结论：

定理：在控制器式（18）和自适应律式（22）的作用下，由式（3）描述的水下航行器纵向运动的深度跟踪误差全局渐近收敛到零，且对未知模型参数具有自适应性。

3 仿真研究

为验证文中提出的自适应反演控制器式（18）和式（22）的有效性，采用REMUS水下航行器的衡重参数和流体力学参数［5］进行数学仿真研究。控制参数和自适应参数为：

初始深度为0m，深度指令为20m。仿真结果如图1～图2所示。

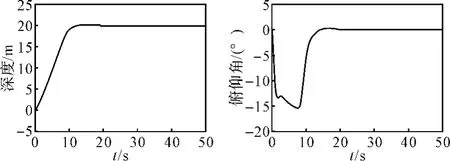
图1 深度仿真曲线 图2 俯仰角仿真曲线

从仿真结果可以看出，深度跟踪误差收敛到零，控制性能良好，并且对未知参数具有自适应性。

4 总结

文中研究了动力学参数不确定情况下的水下航行器纵向运动控制问题，基于自适应反演方法设计出深度跟踪控制器，考虑了深度变化率的幅值限制，选择具有饱和特性的镇定函数。理论分析和仿真结果均表明，该控制器保证了深度跟踪的全局渐近稳定性，并具有参数自适应能力。该设计方法还可应用于水下航行器的定角爬潜和航向控制器的设计中。

［1］徐德民.鱼雷自动控制系统［M］.2版.西安：西北工业大学出版社，2001.

［2］M Krstic，I Kanellakopoulos，P V Kokotovic.Nonlinear and adaptive control design［M］.New York：John Wiley Inc，1995.

［3］Thor I Fossen.Marine control systems［M］.Trondheim，Norway：Marine Cybernetics，2002.

［4］Khoi B Ngo，Robert Mahony，Zhong－Ping Jiang.Integrator backstepping design for motion system with velocity constraint［C］//Proceedings of the 5th Asian Control Conference，2004：141-146.

［5］Timothy Prestero.Verification of a six－degree of freedom simulation model for the REMUS autonomous underwater vehicle［D］.MIT/WHOI Joint Program in O－ceanographic Engineering，2001.