桥基荷载作用下特殊高边坡岩体力学行为三维数值分析
2010-09-19刘学强
刘学强
(福州市规划设计研究院,福建福州 350003)
桥基荷载作用下特殊高边坡岩体力学行为三维数值分析
刘学强
(福州市规划设计研究院,福建福州 350003)
桥基荷载作用下高陡边坡岩体力学行为是桥基位置确定及边坡稳定性分析的基础.基于大型通用软件ANSYS,对桥基荷载作用下特殊高边坡岩体力学行为进行三维有限元分析,研究结果可为荷载作用下高陡桥基边坡稳定性分析及桥基合理位置设计提供理论依据.
桥基荷载;角型高边坡;数值分析;三维有限元
0 引 言
边坡稳定分析是个经典土力学问题.在公路、铁路、土建、水利等工程上都涉及到边坡稳定性分析的问题.目前,边坡稳定分析方法主要有:基于极限平衡理论的整体法和基于弹性理论的有限法.而在实际应用中为解决简单边坡问题通常假设坡面为平面,在此基础上边坡问题被简化成二维进行分析,这种边坡分析没有考虑变形的过程.事实上,边坡的滑动形状为三维状态,而且其破坏形态是随着地质条件而发生变化的.二维分析和三维分析最大区别是在于是否考虑地面和滑动面的形状、岩土特性及滑动面强度等影响边坡的变形因素,三维分析与实际情况较为接近.通常,在山区道路建设中,桥基所处岸坡坡面经常突起呈角型形状,包括地质岩层在面上也是异常复杂,岩层厚度并非等厚度分布,工程中常将坡面呈角型形状的高边坡称作特殊高边坡,此时,普通的平面简化已不能完全真实反映边坡的空间形状和力学性能,其分析结果推广到实际边坡应用中往往存在较大误差.故针对角型高边坡稳定性分析应当采用三维模型.
本文结合某市绕城高速公路一座互通立交作为工程实例,互通主线高架桥基落在下穿匝道路基边坡,下穿匝道路基边坡受地形地物等因素限制呈角型形状,角型高边坡的高度达80 m,主线高架桥梁的设计荷载标准为公路I级.本文以此边坡为例进行数值分析,对特殊高边坡在均质条件下岩体力学行为进行详细研究,获得了特殊高边坡岩体力学行为特征及其变化规律.本研究结果可为荷载作用下高陡桥基边坡稳定性分析及桥基合理位置设计提供理论依据.
1 模型建立
1.1 计算参数
本文数值分析均通过大型通用有限元软件ANSYS10.0来实现[1-3],岩体采用ANSYS自带D-P模型,基础为线弹性,二者力学参数如表1所示[4].

表1 计算参数
1.2 基本模型
首先建立桩土相互作用的三维模型.在进行桩土共同作用分析时考虑土的塑性这一特性是十分必要的,而采用有限元方法可以在沉桩动力分析基础上,考虑土的弹塑性沉桩动力影响及桩土接触面特性,分析桩土体系承受荷载作用后的反应,得到桩及土体内力、应力和变形的基本变化规律[5].对基本模型本文做以下几点假定:①桩体是连续的等截面弹性体;②不考虑桥基成桩过程引起的土体变形;③采用等效线性模型来模拟土体材料的非线性.
特殊均质高边坡分析模型中均包括:①边坡的几何参数;②桥基设计参数.边坡几何参数包括坡高、坡度,分别用H和α表示;桥基埋深用D表示,桥基水平距离用S表示,桥基水平距离是指桥基础外边缘线与坡面的水平距离.
我们分析的工程实例为边坡桥梁桩基为1根,桩径2.0 m.桥基荷载设计参数为:桥梁上部结构为12.5 m、桥宽4×30 m、PC连续箱梁,桥梁荷载考虑箱梁自重、车辆荷载等因素,正常使用极限状态组合竖向力荷载为9 280 kN,桩顶桥基荷载强度 q为2 953 kPa;桥基的宽度为B,桥梁桩基长度为L,桥基所在位置均为中风化岩层.与普通高边坡相比,特殊高边坡多了一个分析参数,即坡顶面夹角(见图1),桥基距离S为顶面交点到基础的垂直距离,即模型中坡顶面三角形顶点到基础前缘的垂直距离.其他基本参数为:H=80 m,α=80°,β=90°,B=10 m,L= 15 m,S=10 m,D=2 m.为定义不同施工阶段,对三维几何体进行网格划分(见图2).

图1 基本几何模型
图2 网格划分示意图
2 结果分析
2.1 边坡岩体应力特征
图3为在竖直荷载作用下特殊均质高边坡岩体应力特征云图.

图3 荷载作用下边坡岩体应力特征云图
从图3中可看出,基底及坡脚出现应力集中现象,边坡内部最大主应力随深度的增加而增加.双临空面导致特殊高边坡 yz向剪应力(图3 b)分布特征发生变化,在坡脚出也明显出现应力集中.取各应力云图基础中心下方的横(z向)、纵(x向)剖面,其结果如图4~图6所示.

图4 最大主应力剖面图纵剖面图
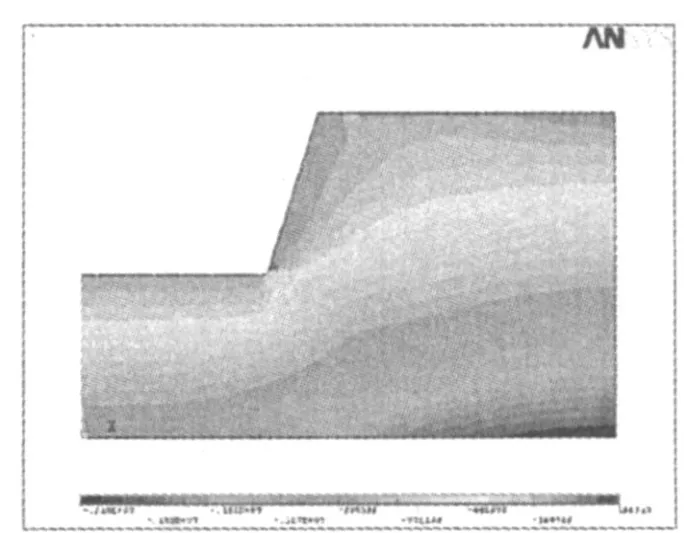
图5 最小主应力剖面图纵剖面图

图6 剪应力剖面图
从最大主应力(图4)和最小主应力(图5)纵剖面云图可看出:在基底及坡脚处均有应力集中现象,最小主应力应力等值线向上凸起;纵剖面剪应力(图6 a)分布特征与一般高边坡大致相同,数值上显示坡脚处剪应力明显减小;受双坡面影响,横剖面剪应力(图6 b)与一般高边坡明显不同,除基底附近外,在两侧坡脚处应力明显集中,并呈对称分布.
2.2 边坡岩体位移特征
竖直荷载作用下特殊均质边坡的位移特征如图7~图9所示.
从图7~图9可以看出:荷载引起的边坡岩体位移均以基础为中心向周围扩散,基础前侧边坡临空面及基础后侧 x向位移程度明显,且均表现出圆弧状分布(见图7 a),这也表明若边坡被破坏,以上两处可能为潜在破坏面两端出口,且破坏面为椭球圆面;y向位移主要向两个临空面发展,即边坡岩体在荷载作用下有向坡面移动的趋势,两坡面交线 y向位移大于同等高度坡面上的位移(见图7 b);同一深度上,坡面附近岩体的水平位移大于边坡内部岩体位移(见图8),在横剖面图上 z向水平位移呈椭圆形对称分布,因双临空面,相对一般高边坡z向水平位移在坡面上也有较大影响;竖直位移在桥基底部最大,向两侧及深部逐渐减小,坡面岩体竖直位移大于同一深度上边坡内部岩体的位移(见图9),在横剖面图上z向竖直位移以基础为中心向周围扩散,z向竖直位移对坡面也有较大影响.

图7 荷载作用下岸坡位移云图
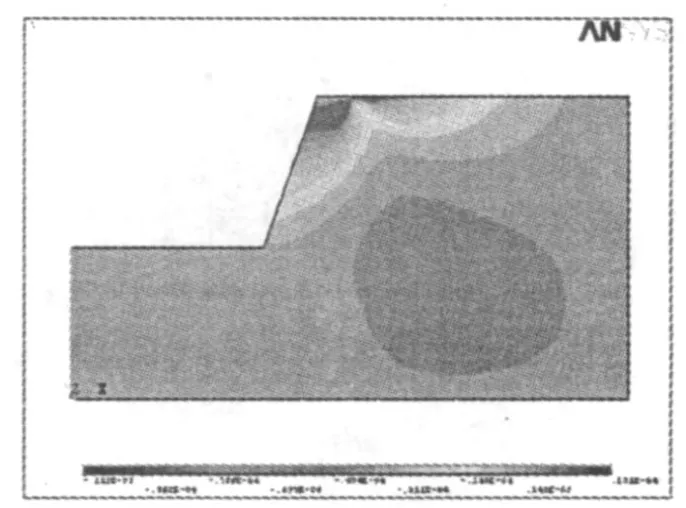
图8 荷载作用下岸坡水平位移纵剖面

图9 荷载作用下岸坡竖直位移纵剖面图
此外,从数值对比可看出,竖直位移要大于水平位移,说明竖直荷载作用下特殊高边坡岩体以竖直位移为主,基底处竖直位移最大,水平位移在两坡面交线处某一位置最大.
3 结 论
通过工程实例对特殊高边坡岩体力学行为特征的分析,我们可以得出以下几点结论:
(1)双临空面导致特殊高边坡yz向剪应力分布特征发生变化,在坡脚处明显出现应力集中.
(2)荷载引起的边坡岩体位移均以基础为中心向周围扩散,基础前侧边坡临空面及基础后侧x向位移程度明显,均表现出圆弧状分布.此表明若边坡被破坏,以上两处可能为潜在破坏面两端出口,且破坏面为椭球圆面.
(3)从数值对比可知,竖直位移要大于水平位移,说明竖直荷载作用下特殊高边坡岩体以竖直位移为主,基底处竖直位移最大,水平位移在两坡面交线处某一位置最大.
(4)根据边坡稳定数值分析结果,本工程的桥梁桥墩桩基入岩深度应不小于12 m,同时,施工时还应对桥基处边坡护面做局部边坡防护.
[1]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,2004.
[2]李裕春,时党勇,赵 远.ANSYS 10.0/LS-DY NA基础理论与工程实践[M].北京:中国水利水电出版社,2006.
[3]李 权.ANSYS在土木工程中的应用[M].北京:人民邮电出版社,2005.
[4]铁道部第一勘测设计院.铁路工程地质手册[S].北京:中国铁道出版社,1999.
[5]黄志全,周 进.单桩桩土作用及其理论计算方法研究[J].山西建筑,2008,34(1):3-4.
Three Dimensional Numerical Analysis of Mechanical Behavior of Rock Mass on Special High Slope under Bridge Load
LIU Xueqiang
(Urban Planning and Design Institute of Fuzhou,Fuzhou 350003,China)
The mechanical behavior of rock mass on high slope under bridge load is the base of bridge position and slope stability analysis.Based on the common software ANSYS,three dimensional numerical analysis of mechanical behavior of rock mass on special high slope under bridge load was made.The results may provide theoretical basis for rational design of bridge position and slope stability analysis.
bridge load;angle high slope;numerical analysis;three-dimensional finite element
U443.15;U416.14
:A
1004-5422(2010)02-0168-04
2010-02-02.
刘学强(1979—),男,工程师,从事桥梁与隧道工程设计.
