模糊PID控制在轮式机器人上的应用

陆磊

0 引言

机器人学代表了机电一体化的最新成就，是当代科学技术发展最活跃的领域之一。轮式机器人是机器人学中的一个重要的分支，它集智能控制系统、环境感知系统、无线通讯系统、运动决策系统于一体。其中，运动控制是轮式机器人研究的关键领域，是轮式机器人进行定位、导航和路径规划的基础。实际应用中，双轮差速机器人的运动控制是基于双闭环的电机控制。控制算法主要有 PID控制、模糊逻辑控制等。但是PID控制算法对非线性系统的控制效果不理想，参数不能实现在线整定，而模糊控制系统的鲁棒性强，干扰和参数变化对控制效果的影响被大大减弱，尤其适合于非线性、时变及纯滞后系统的控制。双轮机器人是一个复杂的非线性系统，其运动过程受诸多非线性因素的影响，如：摩擦系数不同的地面，机器人运动的速度和角速度等。为了使双轮机器人达到好的控制效果，应用模糊控制 PID算法使运动控制系统对非线性影响因素具有一定的自适应能力，实现轮式机器人的速度控制。

1 双轮移动机器人的运动学模型和运动原理

双轮移动机器人的机械结构由车体、两个主动驱动轮、两个从动轮和一个随动轮组成。（如图1）从动轮的作用是精确地计算里程计的数值，随动轮的作用是在运动过程中起支撑作用。机器人在地面的运动可分解为直线运动和旋转运动。在笛卡尔坐标系下，机器人的位姿、速度、角速度用（（x,y,θ）,v,ω）来表示。机器人的运动方程为：

图1 双轮机器人运动学模型

因此，我们只要控制线速度和角速度就可以得到当前小车的位姿。双轮移动机器人完成前进，后退，走直线，左转弯，右转弯等动作的工作原理是通过分别控制左，右轮速度来实现的。基本原理请参考下面几幅图：

图2 双轮机器人结构示意图

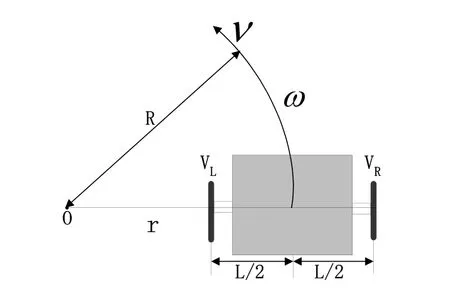
图3 双轮机器人运动示意图

如图2所示，小车采用的是双轮差速驱动模式，D为小车的主动轮左，右轮半径。这种模式可通过分别控制小车的主动轮左、右轮速度来完成各种基本的工作。控制简单，容易实现。在图3中， 可以看出这种运动控制的示意图。如图3所示，V代表小车质心（即中心）的运动速度，Vl代表小车主动轮左轮的运动速度，Vr代表右轮的运动速度。L代表小车的两主动轮轮间距（请参考图2），ω代表小车质心的角速度。Ce 是编码脉冲和轮子速度系数。

小车满足刚体运动的规律，由左右轮之间的物理约束关系，如下运动方程成立：

2 双轮移动机器人的控制模型

速度模式下的系统可以构建出相应的数学模型，用Matlab模拟出传递函数，可以对照实际阶跃相应和构建的数学模型的相应的曲线。其传递函数可以表示为：

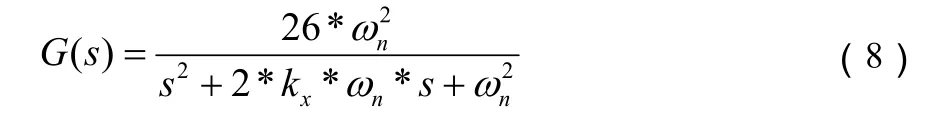
其中 kx＝0.1, ωn=15。

3 在线整定的模糊PID控制系统

3.1 模糊PID控制系统的原理

常规PID控制器的控制算法

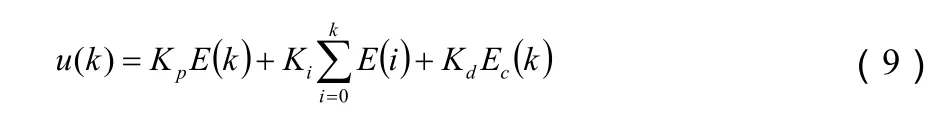
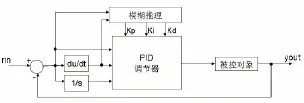
图4 PID参数自组织模糊控制器系统图

其中，E（k）、∑E（i）、Ec（k）分别为被控对象在采样时刻误差、累积误差和误差变化。Kp，Ki，Kd分别为PID的比例，积分和微分的系数。当前应用的常规 PID控制器不具备在线整定控制参数Kp、Ki和Kd的功能，不能满足系统在不同偏差和偏差变化率对 PID参数的自整定要求，因而不适于非线性系统控制。双轮移动机器人是一个复杂的非线性系统，如果选用 PID作为其运动控制器，就应根据实际情况在线整定 PID参数以适应其非线性特征。因此，结合PID算法简单实用和模糊控制能适应非线性系统的优点，基于模糊推理策略在线整定 PID控制参数，提出模糊 PID的运动控制系统。将速度误差和误差变化率作为模糊推理机的输入，然后对PID的三个参数进行在线自整定。图4为PID参数自组织模糊控制器系统原理图。图中，经模糊化处理，得到E，EC，再由模糊控制规则推理得出△Kp，△Ki，△Kd再根据逆模糊化的方法得到Kp，Ki，Kd，修改PID调节器的参数，进而控制被控对象。

3.2 输入输出量模糊化

选择速度的误差E和误差变化率EC的模糊集合作为输入语言变量，选择△Kp，△Ki，△Kd的模糊集合作为输出语言变量，语言值分别定为“负大（NB）”、“负中（NM）”、“负小（NS）”、“零（ZO）”、“正小（PS）”、“正中（PM）”、“正小(PS）”七个等级。并且：

E，EC的基本论域设为：[-3,+3]

△Kp的基本论域设为：[-0.3,+0.3]

△Ki的基本论域设为：[-0.06,+0.06]

△Kd的基本论域设为：[-3,+3]

设实际输入为X，

利用公式10和11，将线速度的误差和线速度的误差变化率进行模糊化处理，使数值化成输入量论域的范围。

3.3 模糊规则的建立

在模糊控制规则表中，各个元素子集都是用字母表示的，而在控制过程中，模糊判决器的输入和输出都是一些数值，因此需要在数值和各个语言变量之间建立联系。各个语言变量都表示一定的范围，这种范围的覆盖面可以用隶属度来表示。隶属度函数有多种形状，有正态分布的，有等腰梯形的，最常用的是三角形，如图5所示。每个语言变量表示的范围可能有所交叉，但除了几个特殊点，一个具体数值隶属于各个字母符号的程度是不一样的。

根据经验总结，被控对象在不同的E和EC状态时参数自适应调整的原则如下：

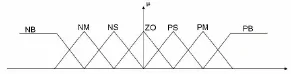
图5 隶属度函数图

（1）当速度偏差较大时，为提高响应速度，消除稳态偏差，Kp取大值，同时为了避免系统出现超调，Ki应取零值；当速度偏差比较小时，为继续减小偏差，防止超调过大产生振荡，Kp值要减小，Ki取小值；当速度偏差很小时，为消除静差，克服超调，使系统尽快稳定，Kp值要继续减小，Ki值不变或稍取大值。

（2）当速度偏差与速度偏差变化率同号时，说明该电机转速是朝偏离其它电机转速方向变化，因此，为使尽快消除偏差，提高响应速度，Kp应取最大值；当偏差与偏差变化率异号时，说明该电机转速是朝靠近其它电机转速方向变化的，因此Kp取值应随偏差减小而逐渐减小。

（3）偏差变化率的大小表明偏差变化的速率。EC越大，Kp取值越小，Ki取值越大，反之亦然。同时要结合偏差大小来考虑。

以△Kp为例，所列模糊控制规则如图 6，△Ki，△Kd可类似推出。再利用max-min法则得到总的输出模糊集合。

图6 △Kp控制规则表

3.4 输出量的解模糊

通过模糊推理得到的结果是一个模糊集合。但是在实际使用中，在推理得到的模糊结合中取一个相对最能代表这个模糊集合的单值过程称作解模糊判决。解模糊判决常用的方法有最大隶属度法、重心法。文中选用面积重心法解模糊：

算法实现为：

4 仿真结果

3个输出量的Matlab仿真流程图如图7

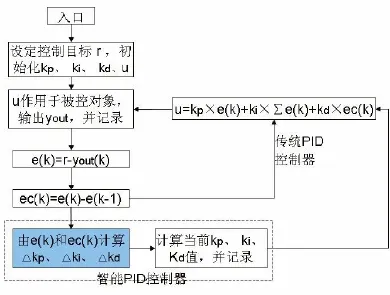
图7 程序流程图表

根据下面的结果，由算式 ：根据模糊后算得修改后的Kp,Ki,Kd完成对控制器的调整。由Matlab仿真的系统阶跃响应曲线如图8所示。从图中结果可以看出，后者比前者具有更快的响应速度更高的稳定性。

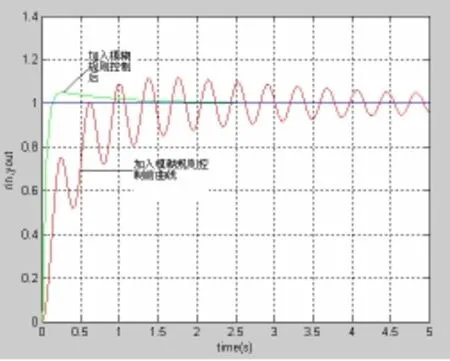
图8 常规PID和Fuzzy-PID控制系统阶跃响应图

采样时间为1ms，在第0.3秒时模糊PID控制器输出加入1.0的干扰，相应响应曲线如图9。

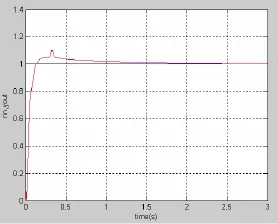
图9 Fuzzy-PID控制系统加入扰动后的阶跃响应图

5 结论

自适应模糊控制整定PID参数是在常规PID算法的基础上，通过计算机器人的速度误差和速度误差变化率，利用模糊推理系统，查询模糊矩阵表进行参数在线调整。仿真结果表明模糊 PID控制器在速度控制、系统稳定性和系统超调方面具有明显的优点。

[1]张铭钧.智能控制技术[M].哈尔滨:哈尔滨工程大学出版社,2006.

[2]刘满禄,张华,王瑗,胡天链.基于模糊控制器的移动机器人导航[J].兵工自动化,2009,28(6):73-75.

[3]黄炳强,曹广益,费燕琼.基于模糊控制器的机器人路径规划研究[J].测控技术,2007,26(1):30-32.

[4]Honghai Liu, Brown DJ, Coghill GM. Fuzzy Qualittaive RobotKinematics[J].Fuzzy Systems,2008,3(16):808-822.