基于受限语料库的语言平滑算法比较研究

孙守安，杨根科，杨祖华

0 引言

机器翻译是使用电子计算机把一种自然语言翻译成另外一种自然语言的一门学科。机器翻译要实现自然语言翻译，必然涉及对自然语言处理，所以机器翻译也是自然语言处理的一个分支。

机器翻译分为规则翻译与统计翻译两大流派。规则翻译系统曾经兴盛一时，但是，由于需要将专家的领域知识融入翻译规则中，并且该方法随着规则库的增大性能明显下降，所以目前还没能出现一种比较完善的表示自然语言的规则系统。而随着计算机速度的加快，统计翻译流派开始崭露头角，并且在最近几年占据了主要地位。统计翻译，又称为数据驱动（data-driven）的机器翻译[1]。

语言模型广泛应用于语音识别、信息抽取以及机器翻译等领域。统计语言模型训练需要具备大量的训练数据，并且要求训练数据和测试数据来源于相同的领域。也就是说，统计语言模型的质量取决于训练文本数据的大小和质量。如果不具备大量的训练数据，或者训练数据与测试数据不匹配，就不能得到精确的统计语言模型。

在很多情况下，即使能够利用大量语料建立一个通用语言模型，但是当用到特定领域的文本翻译任务时, 由于词语的概率分布与模型不相同，系统的效果也大打折扣。而利用受限文本集合，语料库规模较小，往往使语言翻译受到限制。在这种情况下解决数据稀疏问题会变得比较重要。

本文研究了在受限语料库的情况下N-gram的语言模型训练问题。计算文本句子的先验概率需要通过一个较大的语料库来获取。但当语料库是有限的时候，数据的稀疏性成为N元语法模型存在的严重问题。因此，通过数据平滑技术来改善语言模型是目前研究的主流方向。本文通过实验比较了各种平滑方法在受限语料库情况下的性能，来解决数据稀疏问题。通过实验，可以发现，通过选择合理的平滑方法可以降低模型的复杂度以及熵值。

1 N元语法模型的数据稀疏问题

统计机器翻译目的就是针对自然语言领域的语料进行统计推理。通过统计计算相关数据，根据这些数据分布得到一些推论。利用当前词组，也就是历史词组来预测下一个将要出现的词，是处理语法模型问题的核心。通过对已经存在大量的文本的统计，我们可以知道什么样的词会最大概率的出现在当前语串之后。统计自然语言理解中常用的数学模型有 N 元语法模型、隐马尔可夫模型、最大熵模型等。其中N元语法模型更多地用于推测词出现顺序的概率，并且相对简单，效果也较好。

n 元语法模型的基本任务可以看作下面概率方程：

其中WT表示单位词，在这样一个随机问题中，使用了先前词，也就是历史来预测下序列将要出现的词。令 表示词序列，于是有：

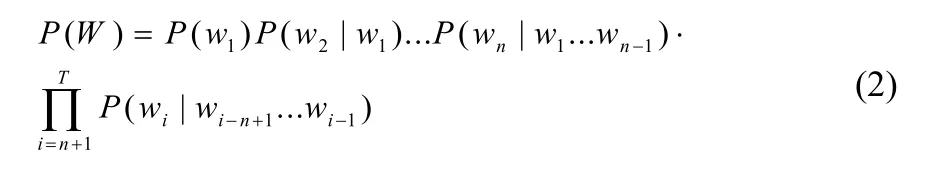
在将一定数量的训练数据归为某些特征类别之后，接下来要做的工作是对这些数据的目标特征进行概率估计。对于N元语法模型的例子，我们感兴趣的是预测任务p ( wi|w1w2… wi−1)与概率 P (w1w2… wi−1wi)之间的关系。

在训练语料库中，尤其是受限语料库中，很多可能事件没有出现。对大量的未知的事件给了一个零值作为估计，不能真实反映现实的语言模型。训练语料库中没有出现的事件，不能说明它们在实际问题中永不出现。在实际计算问题中，零值估计概率的词组导致整个句子的概率是零，无法寻求最优解，导致随机语言模型的算法失败。根据最大似然估计，这些事件的概率为零。然而这些事件的真实概率并非一定为零。这个问题被称为数据稀疏问题。

目前解决模型的数据稀疏问题主要依靠各种平滑方法（smoothing method），包括折扣（discounting）和预测（predicting）两部分。折扣算法主要是对测试语料中出现的词频按照某种方式打一个折扣，从概率总体中分出一部分概率，再以一定的规则分配给未出现的情况，主要包括的算法有：绝对折扣法，相对折扣法以及Good-Turing，Witten-Bell Absolute等。而预测算法，是利用低阶的信息来预测高阶的概率，其重要实现方法有回退 (backoff )和插值(interpolate)。

2 N-gram中的平滑折扣算法

数据平滑技术是统计机器翻译中的重要方法。由于数据稀疏问题严重地制约着统计语言模型的性能，用于解决该问题的数据平滑技术成为统计语言模型的研究热点。

某种数据平滑算法的优劣，可以根据经过该平滑算法处理之后的语言模型的性能而度量出来。语言模型的性能一般根据它在测试文本上的交叉熵(Cross Entropy)或迷惑度(Perplexity)进行度量。

2.1 拉普拉斯法

拉普拉斯法的基本思想是，在运用最大似然估计时，修改样本中事件的实际计数。校样本中不同事件的概率之相小于1。这样就产生了一些剩余概率量，将这些剩余概率量分配未见事件，从而未见事件的估计概率大于0。

其中，r是该n元词组出现的次数，N是语料库存在的n元词组个数，而B是所有可能的n元词组的个数。

考虑到Laplace法则给出的估计方法明显依赖于语言空间的大小。如果在一个较大的语言空间下，存在很多的稀疏矩阵集，那么该法则可能将未知事件分配大量未知的概率。而与现实情况不符。

Laplace方法夸大了未知事件的出现频率。在受限语料库情况下，数据稀疏问题会导致Laplace方法分给未知事件的概率空间过于庞大，以至于不适合用于受限语料库情况下。

2.2 线性折扣法与绝对折扣法

线性折扣法[2]，是利用一个略小于1的常量，乘以非零词组的概率，将一部分概率空间转移到未知事件上。

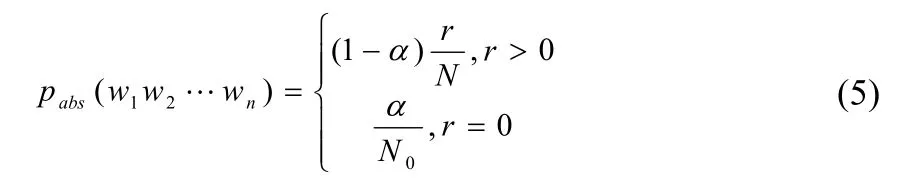
其中，r是该n元词组出现的次数，N是语料库存在的n元词组个数，N0是语料库中未出现的n元词组个数，a是一个小于1的折扣系数。

不过线性折扣法也存在本身的缺陷。因为，一般来说，训练样本中事件频率越高，没有调整过的最大似然估计的准确性越高，线性折扣法并没有体现这一点。不过，绝对折扣法能够体现这一点。

绝对折扣法[2]，是由Ney 与Essen提出来的。在绝对折扣模型中，所有的非零概率都减去一个非常小的常数b，并将其他的概率分配到未知事件上。

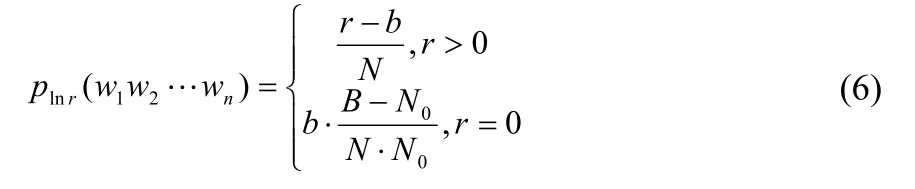
其中，r是该n元词组出现的次数，b是一个小于1的折扣系数，N是语料库存在的n元词组个数，N0是语料库中未出现的n元词组个数。B是所有可能的n元词组的个数。

线性折扣法语绝对折扣法有所差别。绝对折扣模型对高计数事件的作用要小于于对低计数事件的作用，而线性折扣模型对所有已现事件都缩小了一个因数。由于这两个模型算法表达简单清晰，运用很方便。

2.3 Good-Turing法

Good-Turing算法是根据图灵机原理提出的一种确定时间概率或者概率估计的方法。是许多数据平滑技术的核心[3]。Good-Turing算法的基本思想为：假设时间的分布服从二项式分布，对于N-gram模型中出现r次的N元对1inω−+′，根据Good-Turing算法公式，该N元词组出现的次数为r*，如公式所示：

其中nr表示N-gram的训练集中实际出现r次N元词组的个数。那么，对于N-gram中出现次数为r的N元对 的出现概率如公式（8）所示：

2.4 Witten-Bell法

Bell曾提出一系列的平滑算法，用来压缩文本的规模[4]。Witten-Bell方法，也就是他们提到的方法C，在语音语言模型平滑已经有了广泛的应用。该方法的基本思想是：所有的n-gram必须用到n-1 gram做为补偿。

而Witten-bell平滑算法对权重有如下的定义模式：

则权数定义为：

不过，该方法作为语言模型的平滑算法，性能表现略低于前面所提及的平滑算法，尤其是在受限语料库的情况下，该方法所建模型极差。

3 系统实验与仿真

3.1 数据来源

首先收集汉语资料，建立ABC 3个中文语料库。语料库 A来自于专业学科资料化学方面的文本资料。语料库 B作为受限语料库，截取了语料库 A的前半部分。语料库 C作为更受限语料库，截取了语料库B的前半部分。对3个语料库进行了平衡性筛选以及简单错误纠正后，作为后续语料库实验备用。

为了保持一致性，选取材料方向论文集作为测试集，用来测试模型的复杂度[5](Perplexity)。在语料受限的情况下，采用不同的平滑策略会对系统模型产生不同的影响。模型性能的衡量，一般采用模型针对某一测试集的复杂度为标准，这是一种基于平均概率的评判准则[6]。

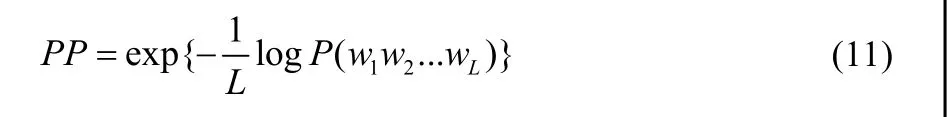
其中，L是测试集中所包含的词数。复杂度PP反映了测试文本相对于该语言模型的不确定性。相差越小，不确定性越小，值越小，说明对于当前模型的不确定性也越小。因此，对于受限的文本翻译问题，其任务就是建立一个模型，使其针对这一领域选出的测试语料有更小的PP值。

评价模型性能另外一个指标是在测试语料集上计算的信息熵。熵的值越大，则学习模型与真实模型的差别也越大，表明模型的效果越差。

语言模型的熵值或迷惑度值越小，说明该平滑算法的性能越好。

3.2 实验结果

通过在CMU-cam平台实验测试，我们可以得到在不同语料库下，系统语言模型的性能表现。4种不同平滑算法在受限程度不同的语料库的性能表现如表1所示。

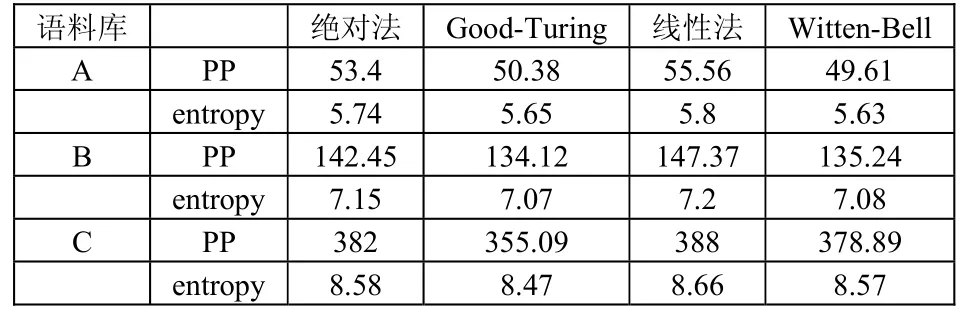
表1 平滑算法结果比较

从表1可以看出，随着训练语料库规模的递减，针对所有的算法，测试集的PP值逐渐增大。这是因为，训练语料库规模越小，所训练出的模型也就越不稳定。测试文本与语言模型的匹配程度也就越来越小，反映在PP值上就是越来越大。

从上面实验数据可以看出。绝对折扣方法一直优于线性折扣方法。训练语料库越小，Good-Turing平滑在四种平滑方法的相对表现也越好。Witten-bell方法作为语音处理中常用的平滑方法，并不适用于文本翻译。

实验结果表明，在大部分情况下，复杂度与熵值存在相互关系，复杂度越大，熵值也越大。在受限语料库问题下，各种平滑算法对模型的性能会有较大的影响。Witten-bell一般要求庞大的训练库资料，所以在受限语料库条件下，表现较差。线性折扣法与绝对折扣法表现居中，而Good-Turing法在语料库较小的情况下优势明显，这是因为Good-Turing法认为高频词组最大似然估计更准确，不对其进行折扣，而低频词组通过期望模型得到观测频率，计算方法与语料库规模的联系比较小，所以适合于受限语料库的情况。

4 结论

用于特定领域的文本翻译系统，往往受到相关文本缺少的困扰，无法通过大规模语料库的建设来训练语言模型。针对这种问题，我们建立了语料库，解决了数据稀疏问题，以及利用已有的高频词组称为提升系统性能的关键问题。本文通过实验比较了各种平滑算法在受限程度不同的语料库的性能，发现语料库的规模对系统性能影响是巨大的，不过利用合理有效的平滑算法可以提升系统的性能。在语料库极度受限的情况下，Good-Turing比其他算法有 5%-10%的性能提升，并且熵值也优于其他算法。针对特定领域受限的语言模型系统，改进与提升Good-Turing算法是一个值得研究的方向，本文的研究结果是以后受限语料库语言模型研究的基础。

[1]刘群.统计机器翻译综述[J].中文信息学报,2004,(19):3.

[2]Ney and Essen. Estimating “small” probabilities by leaving-one-out[J]. IEEE Transactions on pattern analysis and machine intelligence, 1995 ,17 (12):1202-1212.

[3]Gale. Good–Turing frequency estimation without tears[J],Journal of Quantitative Linguistics, 1995,2(3).

[4]Witten I T, Bell T C. The Zero Frequency Problem:Estimating the Probabilities of Novel Events in Adaptive Text Compression [J]. IEEE Transactions on Information Theory , 1991 ,37 (4):1085-1094.

[5]Daniel M. Bikel. On the Parameter Space of Generative Lexicalized Statistical Parsing Models. Ph.D. thesis,University of Pennsylvania. 2004.

[6]杨琳,张建平.颜永红.特定领域的汉语语言模型平滑算法比较研究. 2006,32:14-1.